Maximum and Minimum

There are two different types of extremum (maximum or minimum) values of a function $y=f(x)$. We may consider a value of $y$ that is an extremum globally on the domain or we may also consider a value of $y$ that is an extremum locally around an $x$ value.

A function $f$ has an absolute maximum at $c$ if $f(c)\geq f(x)$ for all $x$ in the domain of $f$. Similarly, $f$ has an absolute minimum at $c$ if $f(c)\leq f(x)$ for all $x$ in the domain of $f$.

A function $f$ has a local maximum (or relative maximum) at $c$ if $f(c)\geq f(x)$ in some neighborhood of $c$ (i.e an open interval that contains $c$). Similarly, $f$ has a local minimum (or relative minimum) at $c$ if $f(c)\leq f(x)$ in some neighborhood of $c$.

Example.

The above figure shows the graph of $f(x)=3x^4-16x^3+18x^2$, $-1\leq x\leq 4$. It has a local maximum at $x=1$ and a local minimum at $x=3$. The local minimum $f(3)=-27$ is also an absolute minimum. $f$ has an absolute maximum $f(-1)=37$. This $f(-1)=37$ is not a local maximum by the way. The reason is that there is no local neighborhood around $x=-1$ as the domain is given by $[-1,4]$.

A natural question one may ask is whether a function always has an absolute maximum and an absolute minimum. You can easily find many examples that show that a function does not necessarily have an absolute maximum or an absolute minimum value. For instance, $y=x$ on $(-\infty,\infty)$ has neither an absolute maximum nor an absolute minimum. The function $y=x^2$ on $[0,1)$ has an absolute minimum 0 at $x=0$ but has no absolute maximum.

Theorem. [Max-Min Theorem, Fermat]
If $f$ is continuous on a closed interval $[a,b]$, then $f$ attains an absolute maximum and an absolute minimum on $[a,b]$.

The following theorem is also due to Fermat.

Theorem. If $f$ has a local maximum or a local minimum at $c$ and if $f'(c)$ exists, then $f'(c)=0$.

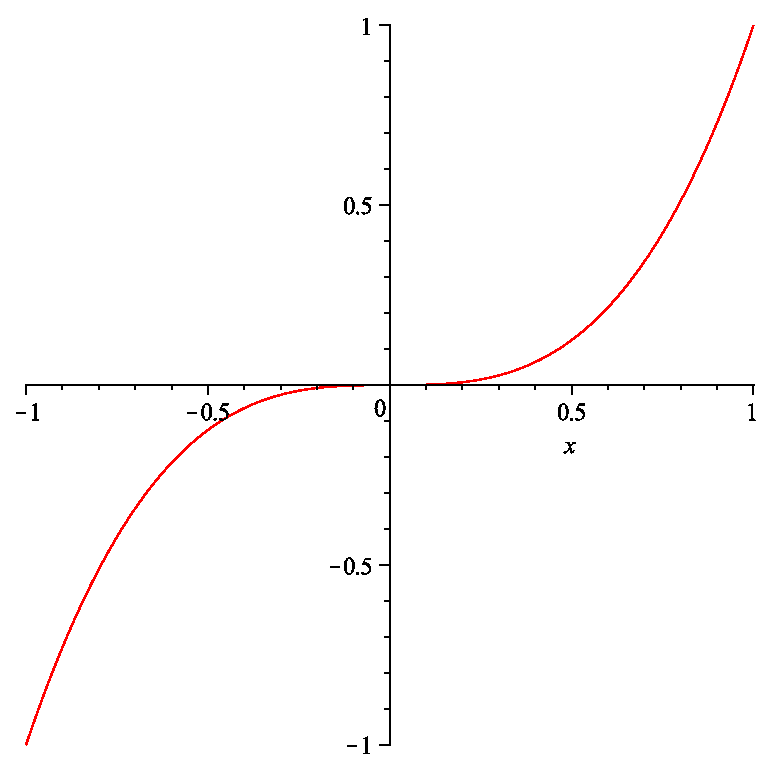
The converse of this theorem is not necessarily true i.e. $f'(c)=0$ does not necessarily mean that $f(c)$ is a local maximum or a local minimum. For example, consider $f(x)=x^3$. $f'(0)=0$ but $f(x)$ has neither a local maximum nor a local minimum at $x=0$ as shown in figure below.

The above theorem is important as an absolute maximum and an absolute minimum may be found among local maximum values, local minimum values and the evaluations of $f$ at the end points, $f(a)$ and $f(b)$. To find local maximum values and local minimum values, we first find points $c$ such that $f'(c)=0$. Such points are called critical points. The reason they are called critical points is that the graph of a function changes from increasing to decreasing or from decreasing to increasing at a critical point.

Definition. A critical point of a function $f(x)$ is a number $c$ in the domain of $f$ such that either $f'(c)=0$ or $f'(c)$ does not exist.

Recipe of Finding Absolute Maximum and Absolute Minimum

Let $f$ be a continuous function on a closed interval $[a,b]$.

Step 1. Find all critical points of $f$ in $(a,b)$.

Step 2. Evaluate $f$ at each critical point obtained in Step 1.

Step 3. Find $f(a)$ and $f(b)$.

Step 4. Compare all the values obtained in Steps 2 and 3. The largest value is the absolute maximum and the smallest value is the absolute minimum.

Example. Find the absolute maximum and the absolute minimum values of
$$f(x)=x^3-3x^2+1,\ -\frac{1}{2}\leq x\leq 4.$$

Solution.

Step 1. Find all critical points of $f$ in $\left(-\frac{1}{2},4\right)$.

$f'(x)=3x^2-6x$. Set $f'(x)=0$ i.e. $3x^2-6x=0$. $3x^2-6x$ is factored as $3x(x-2)$. So we find two critical points $0, 2$.

Step 2. Evaluate $f$ at each critical point obtained in Step 1.

$f(0)=1$ and $f(2)=-3$.

Step 3. Find $f\left(-\frac{1}{2}\right)$ and $f(4)$.

$f\left(-\frac{1}{2}\right)=\frac{1}{8}$ and $f(4)=17$.

Step 4. Compare all the values obtained in Steps 2 and 3.

The largest value is $f(4)=17$ so this is the absolute maximum value of $f$ on $\left[-\frac{1}{2},4\right]$. The smallest value is $f(2)=-3$ so this is the absolute minimum of $f$ on $\left[-\frac{1}{2},4\right]$.