Linear Approximation
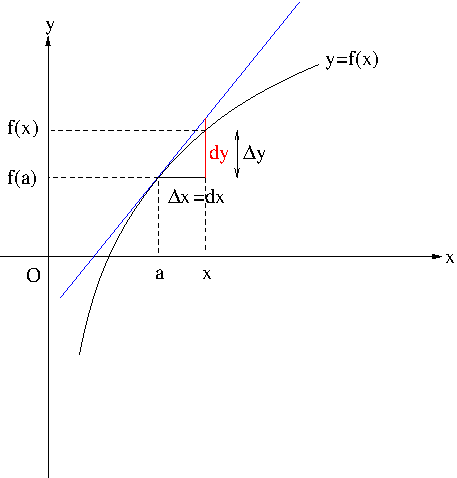
Figure 1. Linear Approximation
Let $y=f(x)$ be a differentiable function. The function $f(x)$ can be approximated by the tangent line to $y=f(x)$ at $a$ if $x$ is near $a$. Such an approximation is called a linear approximation.
If $x\approx a$ then $\Delta x=x-a\approx 0$, so we have
\begin{align*}
\frac{\Delta y}{\Delta x}&\approx \frac{dy}{dx}\\
&=f'(a).
\end{align*}
This means that
$$\frac{f(x)-f(a)}{x-a}\approx f'(a),$$
i.e.
\begin{equation}
\label{eq:lineapprox}
f(x)\approx f(a)+f'(a)(x-a).
\end{equation}
The equation \eqref{eq:lineapprox} is called the linear approximation or tangent line approximation of $f$ at $a$. The linear function
\begin{equation}
L(x):=f(a)+f'(a)(x-a)
\end{equation}
is called the linearization of $f$ at $a$. Notice that $L(x)$ is the equation of tangent line to $f$ at $a$.
Example. Find the linearlization of $f(x)=\sqrt{x+3}$ at $a=1$ and use it to approximate $\sqrt{3.98}$ and $\sqrt{4.05}$.
Solution. $f'(x)=\frac{1}{2\sqrt{x+3}}$, so
\begin{align*}
L(x)&=f(1)+f'(1)(x-1)\\
&=2+\frac{1}{4}(x-1)\\
&=\frac{x}{4}+\frac{7}{4}.
\end{align*}
When $x\approx 1$, we have the approximation
$$\sqrt{x+3}\approx \frac{x}{4}+\frac{7}{4}.$$
Setting $x+3=3.98$ we find $x=0.98$. Hence,
\begin{align*}
\sqrt{3.98}&\approx \frac{0.98}{4}+\frac{7}{4}\\
&=1.995.
\end{align*}
Setting $x+3=4.05$ we find $x=1.05$. Hence,
\begin{align*}
\sqrt{4.05}&\approx \frac{1.05}{4}+\frac{7}{4}\\
&=2.0125.
\end{align*}
Example. Use linear approximation to estimate $\sqrt{99.8}$.
Solution. In order to use linear approximation we need to choose $f(x)$, $x$ and $a$. First clearly from the given quantity we see that $f(x)=\sqrt{x}$ and thereby $x=99.8$. Since $f'(x)=\frac{1}{2\sqrt{x}}$, the linear approximation of $\sqrt{99.8}$ at $a$ is $$\sqrt{99.8}\approx \sqrt{a}+\frac{1}{2\sqrt{a}}(99.8-a)$$ How do we choose a suitable $a$? There are two criteria you have to have in mind. One is $a$ has to be close to $x$ for the linear approximation to be useful. Second $a$ needs to be chosen so that $f(a)$ and $f'(a)$ can be calculated easily (meaning by hand without aid of a calculator). Why is this important? You have to understand that the use of linear approximation is not assuming any use of a calculator. (If you can use a calculator, what is the point of doing this approximation?) This is a method that was developed when there were no calculators available so people could calculate values like $\sqrt{99.8}$ by hand. Considering the two criteria, we find that $a=100$ is the one. Hence, $$\sqrt{99.8}\approx \sqrt{100}+\frac{1}{2\sqrt{100}}(99.8-100)=10+\frac{1}{20}(-0.2)=9.99$$
Example. Use linear approximation to estimate $\cos 29^\circ$.
Solution. $f(x)=\cos x$ and $x=29^\circ=\frac{29\pi}{180}$ ($29^\circ$ is not a number but $\frac{29\pi}{180}$ is). Since $f'(x)=-\sin x$, the linear approximation of $\cos 29^\circ$ at $a$ is $$\cos 29^\circ\approx \cos a-\sin a \left(\frac{29\pi}{180}-a\right)$$ The suitable $a$ is $=\frac{30\pi}{180}=\frac{\pi}{6}$ in the spirit of the two criteria we discussed in the example above. Therefore, we have $$\cos 29^\circ\approx \cos\frac{\pi}{6}-\sin\frac{\pi}{6}\left(-\frac{\pi}{180}\right)=\frac{\sqrt{3}}{2}+\frac{\pi}{360}$$
Differentials
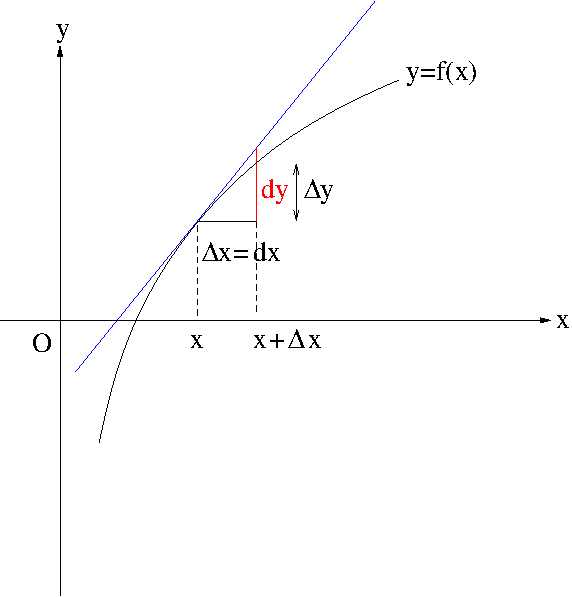
As seen in Figure 3 above, when $\Delta x\approx 0$, $\Delta x=dx$ and $\Delta y\approx dy$. On the other hand, $\frac{dy}{dx}=f'(x)$. Hence, we obtain
\begin{equation}
\label{eq:differential}
\Delta y\approx dy=f'(x)dx=f'(x)\Delta x.
\end{equation}
Example. The radius of a sphere was measured and found to be 21 cm with a possible error in measurement of at most 0.05 cm. What is the maximum error in using this value of the radius to compute the volume of the sphere?
Solution. Let $V$ denote the volume of a sphere of radius $r$. Then $V=\frac{4}{3}\pi r^3$. What we are trying to find is $\Delta V$ with $\Delta r\leq 0.05$ cm. As seen in \eqref{eq:differential}, $\Delta V\approx dV$, so we find $dV$ instead because finding $dV$ is easier than findingthe exact error $\Delta V$. Differentiating $V$ with respect to $r$, we obtain
\begin{align*}
\Delta V&\approx dV\\&=4\pi r^2 dr\\
&=4\pi r^2\Delta r\\
&\leq 4\pi\cdot(21)^2\cdot 0.05\\
&=277.
\end{align*}
So the maximum error in the calculated volume is about 277 $\mbox{cm}^3$.
Linear approximation and differentials may appear to be different entities but the two methods are indeed equivalent and they serve the same purpose. To illustrate this, let us take a look at the following example which will be answered by linear approximation and differentials.
Example. Approximate $\sqrt{81.1}$.
Solution by Linear Approximation. Let $f(x)=\sqrt{x}$ and choose $a=81$. The reason for this choice of $a$ is that one can easily calculate without the aid of a calculator (which is the main point of using this method) and also $a=81$ is close to 81.1. Now we find the tangent line to $f(x)$ at $a=81$, or equivalently the linear approximation $L(x)$ at $a=81$. It is $$L(x)=\frac{1}{2\cdot 9}(x-81)+9$$ Then \begin{align*}L(81.1)&=\frac{1}{18}(81.1-81)+9\\&=\frac{1}{180}+9\\&=9.005555555555556\end{align*} approximates $\sqrt{81.1}$.
Solution by Differentials. Recall that $\Delta y=f(x+\Delta x)-f(x)$ is approximated by the differential $dy=f'(x)dx=f'(x)\Delta x$ for very small $\Delta x$. Now with $f(x)=\sqrt{x}$, $dy=\frac{1}{2\sqrt{x}}\Delta x$. From $\Delta y\approx dy$, we have $$f(x+\Delta x)\approx f(x)+\frac{1}{2\sqrt{x}}\Delta x$$ If we set $f(x+\Delta x)=\sqrt{81.1}$, we can choose $x=81$ and $\Delta x=0.1$. Accordingly, we find \begin{align*}\sqrt{81.1}&\approx\sqrt{81}+\frac{1}{2\sqrt{81}}0.1\\&=9+\frac{1}{180}=9.005555555555556\end{align*}

Pingback: Approximating Functions with Polynomials | MathPhys Archive