Let us begin with the following example.
Example. In how many ways can 8 horses finish in a race? Here, we assume that there are no ties.
Solution. $8\times 7\times 6\times 5\times 4\times 3\times 2\times 1=40,320$ ways.
The example above shows an ordered arrangement. Such an ordered arrangement is called a permutation.
Definition. $n$ factorial $n!$ is defined by
\begin{align*} n!&=n(n-1)(n-2)\cdots 3\cdot 2\cdot 1,\ n\geq 1\\ 0!&=1 \end{align*}
The number of permutation of $n$ objects is $n!$.
Example. There are $6!$ permutations of the six letters of the word “square”. In how may of them is $r$ the second letter?
Solution. $5\times 1\times 4!=5!=120$.
Example. Five different books are on a shelf. In how many different ways can you arrange them?
Solution. $5!=120$.
We now consider the permutation of a set of objects taken from a larger set. Suppose we have $n$ items. The number of ordered arrangements of $k$ items from the $n$ items can be then found by
$$n(n-1)(n-2)\cdots (n-k+1)=\frac{n!}{(n-k)!}$$
Denote this by ${}_nP_k$.
Example. How many license plates are there that starts with three letters followed by 4 digits (no repetitions)?
Solution. \begin{align*} {}_{26}P_3\times {}_{10}P_4&=\frac{26!}{23!}\times\frac{10!}{6!}\\
&=26\cdot 25\cdot 24\cdot 10\cdot 9\cdot 8\cdot 7\\
&=78,624,000
\end{align*}
Example. How many five-digit zip codes can be made where all digits are different? The possible digits are 0-9.
Solution. ${}_{10}P_5=\frac{10!}{5!}=30,240$.
Circular permutations are ordered arrangements of objects in a circle. Suppose that circular permutations such as
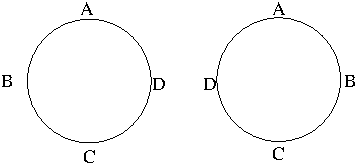
are considered as different. Under this assumption, let us consider seating $n$ different objects in a circle. There are $n!$ ways to arrange $n$ seats in a circle depending on where we start and there are $n$ different ways to start seating, so there are $\frac{n!}{n}=(n-1)!$ circular permutations. If the orientation does not matter, i.e. if we consider clockwise and counterclockwise directions are the same, there are $\frac{(n-1)!}{2}$ circular permutations.
Example. In how many ways can you seat 6 persons at a circular dinner table?
Solution. $(6-1)!=5!=120$.
Suppose that we are interested in counting the number of ways to choose $k$ objects from $n$ distinct objects without regard to order. It can be calculated as
$$\frac{{}_nP_k}{k!}=\frac{n!}{k!(n-k)!}$$
This is denoted by ${}_nC_k$ or $\begin{pmatrix}n\\k\end{pmatrix}$ and is read “$n$ choose $k$”.
Example. From a group of 5 women and 7 men, how many different committees consisting of 2 women and 3 men can be formed? What if two of the men are feuding and refuse to serve on the committee together?
Solution. For the first question, there are
\begin{align*} {}_5C_2\times {}_7C_3&=\frac{5!}{2!3!}\times\frac{7!}{3!4!}\\ &=350 \end{align*}
such committees. For the second question, the number of ways to two feuding men and another man is ${}_2C_2\times {}_5C_1=5$. So, the number of selecting male committee members that do not include the two feuding men together is ${}_7C_3-5=30$. Consequently, the number of possible committees in this case is ${}_5C_2\times 30=300$.
Theorem. Suppose that $n$ and $k$ are integers such that $0\leq k\leq n$. Then
- ${}_nC_0={}_nC_n=1$ and ${}_nC_1={}_nC_{n-1}=n$.
- ${}_nC_k={}_nC_{n-k}$.
- Pascal’s identity: ${}_{n+1}C_k={}_nC_{k-1}+{}_nC_k$.
Proof. 2. $${}_nC_{n-k}=\frac{n!}{(n-k)!(n-(n-k))!}=\frac{n!}{(n-k)!k!}={}_nC_k$$
- \begin{align*} {}_nC_{k-1}+{}_nC_k&=\frac{n!}{(k-1)!(n-k+1)!}+\frac{n!}{k!(n-k)!}\\ &=\frac{n!k}{k!(n+1-k)!}+\frac{n!(n+1-k)}{k!(n+1-k)!}\\ &=\frac{(n+1)!}{k!(n+1-k)!}\\ &={}_{n+1}C_k
\end{align*}
The Pascal’s identity allows us to construct the Pascal’s triangle.
$$\begin{array}{cccccccccc}
n & & & & & & & & &\\
0 & & & & & 1 & & & &\\
1 & & & & 1 & & 1 & & &\\
2 & & & 1 & & 2 & & 1 & &\\
3 & & 1 & & 3 & & 3 & & 1 &\\
4 & 1 & & 4 & & 6 & & 4 & & 1
\end{array}$$
Example. The chess club has six members. In how many ways
- can all six members line up for a picture?
- can they choose a president and a secretary?
- can they choose three members to attend a regional tournament with no regard to order?
Solution.
- ${}_6P_6=6!=720$.
- ${}_6P_2=\frac{6!}{4!}=30$.
- ${}_6C_3=\frac{6!}{3!3!}=20$.
Theorem. (Binomial Theorem) Let $n$ be a nonnegative integer. Then
$$(x+y)^n=\sum_{k=0}^n{}_nC_k x^{n-k}y^k$$
Proof. We prove it by induction on $n$. For $n=0$,
$$(x+y)^0=1=\sum_{k=0}^0 {}_0C_k x^{-k}y^k$$ For $n=1$, $$\sum_{k=0}^1 {}_1C_k x^{1-k}y^k=x+y$$ Suppose the statement is true up to $n$, i.e. $$(x+y)^n=\sum_{k=0}^n{}_nC_k x^{n-k}y^k$$ \begin{align*} (x+y)^{n+1}&=(x+y)^n(x+y)\\ &=\sum_{k=0}^n {}_nC_k x^{n-k}y^k\\ &=\sum_{k=0}^n {}_nC_kx^{n+1-k}y^k+\sum_{k=0}^n {}nC_k x^{n-k}y^{k+1}\\ &=\sum_{k=0}^n {}_nC_kx^{n+1-k}y^k+\sum_{k=1}^{n+1} {}_nC{k-1} x^{n+1-k}y^k\ (\mbox{replaing $k$ by $k-1$ in the second sum})\\ &={}_nC_0x^{n+1}+\sum_{k=1}^n[{}_nC_k+{}_nC{k-1}]x^{n+1-k}y^k+{}_nC_n y^{n+1}\\ &={}_{n+1}C_0 x^{n+1}+\sum_{k=1}^n {}_{n+1}C_k x^{n+1-k}y^k+{}_{n+1}C_{n+1} y^{n+1}\ (\mbox{Pascal’s identity})\\
&=\sum_{k=0}^{n+1}{}_{n+1}C_k x^{n+1-k}y^k
\end{align*}
This completes the proof.
Example. Expand $(x+y)^6$ using the Binomial Theorem.
Solution.
$$(x+y)^6=x^6+6x^5y+15x^4y^2+20x^3y^3+15x^2y^4+6xy^5+y^6$$
Example. How many subsets are there of a set with $n$ elements?
Solution. There are ${}nC_k$ subsets of $k$ elements, $0\leq k\leq n$. Hence, the total number of subsets of a set of $n$ elements is $$\sum_{k=0}^n {}_nC_k=(1+1)^n=2^n$$
References:
Marcel B. Finan, A Probability Course for the Actuaries
Sheldon Ross, A First Course in Probability, Fifth Edition, Prentice Hall, 1997
