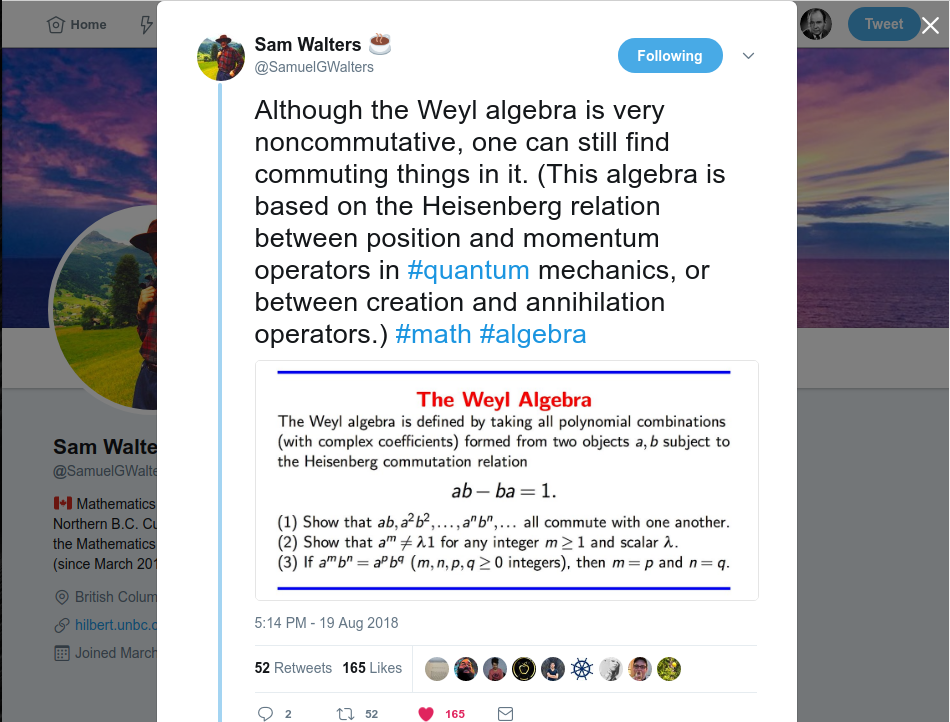
Sam Walters twitted another inspiring math tweet. This time it is about Weyl Algebra. Roughly speaking Weyl algebra is the free algebra generated by two objects $a$ and $b$ which satisfy the Heisenberg commutation relation $$ab-ba=1$$ This commutation relation is originated from the canonical commutation relation $$qp-pq=i\hbar 1$$ in quantum mechanics. Here $p$ and $q$ represent the momentum and the position operators. Although it is commonly called Weyl algebra, its idea appears to have originated from P.A.M. Dirac [1] and for that reason it is also called Dirac’s quantum algebra. In his tweet, Sam stated three properties regarding Weyl algebra to prove as seen in the screenshot below.
So far I have been able to prove the properties (1) and (2). Their proofs follow. If/when I prove the property (3), I will included its proof here as an update.
(1) Show that $ab,a^2b^2,\cdots,a^nb^n,\cdots$ all commute with one another.
Proof. First we show by induction on $n$ that \begin{equation}\label{eq:commut}(ab)(a^nb^n)=(a^nb^n)(ab)\end{equation} for all $n=1,2,\cdots$. Suppose that \eqref{eq:commut} is true for $n=1,\cdots,k$. \begin{align*}(ab)(a^{k+1}b^{k+1})&=(ab)a(a^kb^k)b\\&=a(ba)(a^kb^k)b\\&=a(ab+1)(a^kb^k)b\\&=a(ab)(a^kb^k)b+a(a^kb^k)b\end{align*} Similarly, we show $$(a^{k+1}b^{k+1})(ab)=a(a^kb^k)(ab)b+a(a^kb^k)b$$ By induction hypothesis, we have $$(ab)(a^{k+1}b^{k+1})=(a^{k+1}b^{k+1})(ab)$$ Hence it completes the proof of \eqref{eq:commut}.
Now we show that \begin{equation}\label{eq:commut2}(a^kb^k)(a^mb^m)=(a^mb^m)(a^kb^k)\end{equation} for all $k,m=1,2,\cdots$. Fix $k$ and we do induction on $m$. Suppose \eqref{eq:commut2} is true for all $m=1,\cdots,l$. \begin{align*}(a^{l+1}b^{l+1})(a^kb^k)&=a^l(ab)b^l(a^kb^k)\\&=a^l(1+ba)b^l(a^kb^k)\\&=(a^lb^l)(a^kb^k)+a^l(ba)b^l(a^kb^k)\end{align*} Similarly we show that $$(a^kb^k)(a^{l+1}b^{l+1})=(a^kb^k)(a^lb^l)+(a^kb^k)a^l(ba)b^l$$ Thus we are done if we can show that $$a^l(ba)b^l(a^kb^k)=(a^kb^k)a^l(ba)b^l$$ For $l=1$, this is clear by \eqref{eq:commut}. Assume that $l>1$. \begin{align*}a^l(ba)b^l(a^kb^k)&=a^lb(ab)b^{l-1}(a^kb^k)\\&=a^lb(1+ba)b^{l-1}(a^kb^k)\\&=(a^lb^l)(a^kb^k)+a^lb^2(ab)b^{l-2}(a^kb^k)\\&=(a^lb^l)(a^kb^k)+a^lb^2(1+ba)b^{l-2}(a^kb^k)\\&=2(a^lb^l)+a^lb^3ab^{l-2}(a^kb^k)\\&=(l-1)(a^lb^l)(a^kb^k)+(a^lb^l)(ab)(a^kb^k)\end{align*} Similarly we show that $$(a^kb^k)a^l(ba)b^l=(l-1)(a^kb^k)(a^lb^l)+(a^kb^k)(a^lb^l)(ab)$$ The induction hypothesis and \eqref{eq:commut} then conclude the proof of \eqref{eq:commut2}.
Lemma. \begin{align}\label{eq:commut3}[a^k,b]&=a^kb-ba^k=ka^{k-1}\\\label{eq:commut4}[a,b^k]&=kb^{k-1}\end{align}
Proof. We prove only \eqref{eq:commut3} as \eqref{eq:commut4} can be proved similarly. $k=1$ is the commutation relation. Assume that $k>1$. \begin{align*}a^kb-ba^k&=a^{k-1}(ab)-ba^k\\&=a^{-1}(1+ba)-ba^k\\&=a^{k-1}+a^{k-1}ba-ba^k\\&=a^{k-1}+a^{k-2}(ab)a-ba^k\\&=a^{k-1}+a^{k-2}(1+ba)a-ba^k\\&=2a^{k-1}+a^{k-2}ba^2-ba^k\end{align*} Continuing this process we arrive at $$a^kb-ba^k=ka^{k-1}$$
Short Proof. One can prove \eqref{eq:commut3} and \eqref{eq:commut4} straightforwardly using the formula $$p(a)b-bp(a)=p'(a)$$ for any polynomial $p$, which is discussed here.
(2) Show that $a^m\ne\lambda 1$ for any integer $m\geq 1$ and scalar $\lambda$.
Proof. We prove by contradiction. Suppose that $a^m=\lambda 1$ for some $m\geq 1$ and a scalar $\lambda\ne 0$. If $m=1$, then $ab-ba=0$ so a contradiction. Thus it must be that $m>1$. $[a^m,b]=[\lambda 1,b]=0$. But by \eqref{eq:commut3} $[a^m,b]=ma^{m-1}$. This means that $a^{m-1}=0$ which is a contradiction because $\lambda 1=a^m=a^{m-1}a=0$.
(3) If $a^mb^n=a^pb^q$ ($m,n,p,q\geq 0$) then $m=p$ and $n=q$.
Proof. Suppose that $m\ne p$. Without loss of generality one may assume that $m>p$ i.e. $m=p+k$ for some $k\geq 1$. Then $a^mb^n=a^pb^q\Longrightarrow a^p(a^kb^n-b^q)=0$. Weyl algebra has no zero divisors (see for example [2] where it is proved using degree argument) and $a^p\ne 0$ by the property (2). So $a^kb^n-b^q=0$. Since $b^q$ commutes with $b$, so does $a^kb^n$ i.e. $a^kb^{n+1}-ba^kb^n=0$. This implies that $ka^{k-1}=[a^k,b]=0$. A contradiction!. Therefore, $m=p$. One can show that $n=q$ in a similar manner.
Update: A twitter user named Long offered a brilliant proof for (1). I reproduce his/her proof here. Let $x=ab$. Then one can easily show by induction on $n$ that $a^nx=(x+n)a^n$ and $xb^n=b^n(x+n)$ for $n=1,2,\cdots$. Now \begin{align*}a^{n+1}b^{n+1}&=a^nxb^n\\&=(x+n)a^nb^n\\&=(x+n)(x+n-1)\cdots (x+1)x\end{align*} This means $a^nb^n$ for all $n=1,2,\cdots$ belong to the commutative subalgebra of Weyl algebra generated by $x=ab$.
References:
- P.A.M. Dirac, The fundamental equations of quantum mechanics, Proc. Roy. Soc. A, v.109, pp.642-653, 1925
- S. C. Coutinho, A Primer of Algebraic D-modules, London Mathematical Society Student Texts 33, Cambridge University Press, 1995