The following theorem is something one can easily picture intuitively.
Theorem. [Rolle’s Theorem]
Let $f$ be continuous on the closed interval $[a,b]$ and differentiable on the open interval $(a,b)$. If $f(a)=f(b)$, then there exists a number $c$ in $(a,b)$ such that $f'(c)=0$.
Example. Show that the equation $x^3+x-1=0$ has exactly only one real root.
Solution. Let $f(x)=x^3+x-1$. Note that $f(0)=-1$ and $f(1)=1$. So by the Intermediate Value Theorem, we see that there exists at least a root of the equation $x^3+x-1=0$ in the interval $(0,1)$. Now suppose that there are two different roots $a$ and $b$ of the equation $x^3+x-1=0$. Without loss of generality, we may assume that $a<b$. Then $f(x)$ is continuous on $[a,b]$ and differentiable on $(a,b)$. By Rolle’s Theorem then, there exist a number $c$ in $(a,b)$ such that $f'(c)=0$. However, $f'(x)=3x^2+1\geq 1$ for all real number $x$. This is a contradiction. Therefore, there should be only one root of the equation.
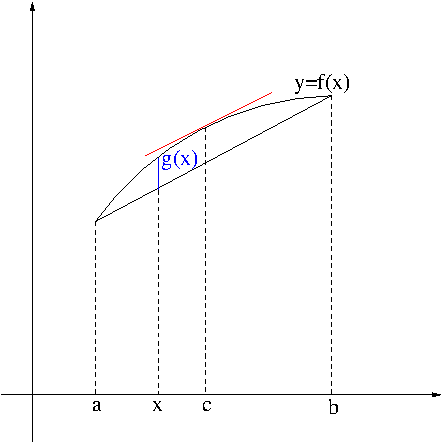
Let $f$ be continuous on $[a,b]$ and differentiable on $(a,b)$. Define $g(x)$ to be the distance between $f(x)$ and the line segment from $(a,f(a))$ to $(b,f(b))$, i.e.
$$g(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a).$$ Then $g(x)$ is continuous on $[a,b]$ and differentiable on $(a,b)$. Since $g(a)=g(b)=0$, by Rolle’s theorem there exists a number $c$ in $(a,b)$ such that $g'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}=0$. Therefore, we proved the following theorem.
Theorem. [Mean Value Theorem]
Let $f$ be continuous on $[a,b]$ and differentiable on $(a,b)$. Then there exists a number $c$ in $(a,b)$ such that
$$f'(c)=\frac{f(b)-f(a)}{b-a}.$$
Remark. Why the name Mean Value Theorem? The average $\mathrm{av}(f)$ of a continuous function $f$ on a closed interval $[a,b]$ can be defined by $$\mathrm{av}(f)=\frac{1}{b-a}\int_a^b f(x)dx$$ See here for details. If $f'(x)$ is continuous on $[a,b]$, its average on $[a,b]$ is given by $$\frac{1}{b-a}\int_a^bf'(x)dx=\frac{f(b)-f(a)}{b-a}$$ That is, Mean Value Theorem states that one of the values of $f'(x)$ on $(a,b)$ becomes the average of $f'(x)$ on $[a,b]$.
The following examples are applications of the Mean Value Theorem.
Example. Suppose that $f(0)=-3$ and $f'(x)\leq 5$ for all values of $x$. How large can $f(2)$ possibly be?
Solution. By the Mean Value Theorem, there exists a number $c$ in $(0,2)$ such that
$$f'(c)=\frac{f(2)-f(0)}{2-0}=\frac{f(2)+3}{2}.$$
Since $f'(c)\leq 5$,
\begin{align*}
f(2)&=2f'(c)-3\\
&\leq 2\cdot 5-3=7.
\end{align*}
Hence, $7$ is the largest possible value of $f(2)$.
Example. A trucker handed in a ticket at a toll booth showing in 2 hours she had covered 159 mi on a toll road with speed limit of 65 mph. The trucker was cited for speeding. Why?
Solution. The average speed was $\frac{159}{2}=79.5$ mph. By the Mean Value Theorem the trucker was driving at the speed 79.5 mph at some point .
Using Mean Value Theorem, one can prove the following theorem. The proof is straightforward and is left for readers.
Theorem. If $f'(x)=0$ for all $x$ in the open interval $(a,b)$, then $f$ is constant on $(a,b)$.

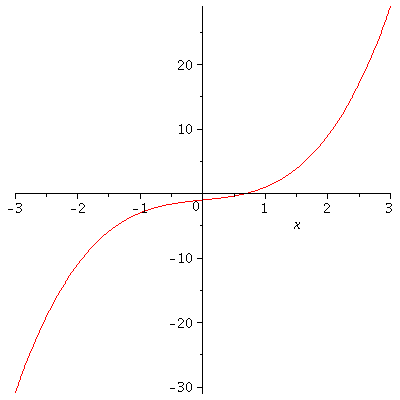
Pingback: Approximating Functions with Polynomials | MathPhys Archive