If given integration takes the form $\int f(g(x))g'(x)dx$ then it can be converted to a simpler integration that we may be able to evaluate by the substitution $u=g(x)$. In fact, the integration is given in terms of the new variable $u$ as
$$\int f(g(x))g'(x)dx=\int f(u)du.$$
Example. Evaluate $\int x\sqrt{1+x^2}dx$.
Solution. Let $u=1+x^2$. Then $du=2xdx$. So,
\begin{align*}
\int x\sqrt{1+x^2}dx&=\frac{1}{2}\int\sqrt{u}du\\
&=\frac{1}{3}u^{\frac{3}{2}}+C\\
&=\frac{1}{3}(1+x^2)^{\frac{3}{2}}+C,
\end{align*}
where $C$ is an arbitrary constant.
Example. Evaluate $\int\cos (7\theta+5)d\theta$.
Solution. Let $u=7\theta+5$. Then $du=7d\theta$. So,
\begin{align*}
\int\cos (7\theta+5)d\theta&=\frac{1}{7}\int\cos udu\\
&=\frac{1}{7}\sin u+C\\
&=\frac{1}{7}\sin(7\theta+5)+C,
\end{align*}
where $C$ is an arbitrary constant.
Example. Evaluate $\int x^2\sin(x^3)dx$.
Solution. Let $u=x^3$. Then $du=3x^2dx$. So,
\begin{align*}
\int x^2\sin(x^3)dx&=\frac{1}{3}\int \sin udu\\
&=-\frac{1}{3}\cos u+C\\
&=-\frac{1}{3}\cos(x^3)+C,
\end{align*}
where $C$ is an arbitrary constant.
Example. Integrals of $\sin^2x$ and $\cos^2x$.
- \begin{align*}\int\sin^2xdx&=\int\frac{1-\cos 2x}{2}dx\\&=\frac{x}{2}-\frac{\sin 2x}{4}+C\end{align*}
- \begin{align*}\int\cos^2xdx&=\int\frac{1+\cos 2x}{2}dx\\&=\frac{x}{2}+\frac{\sin 2x}{4}+C\end{align*}
How do we evaluate a definite integral of the form $\int_a^b f(g(x))g'(x)dx$? The following example shows you how.
Example. Evaluate $\int_{-1}^1 3x^2\sqrt{x^3+1}dx$.
Solution. First let us calculate the indefinite integral $\int 3x^2\sqrt{x^3+1}dx$. Let $u=x^3+1$. Then $du=3x^2dx$. So,
\begin{align*}
\int 3x^2\sqrt{x^3+1}dx&=\int\sqrt{u}du\\
&=\frac{2}{3}u^{\frac{3}{2}}+C\\
&=2(x^3+1)^{\frac{3}{2}}+C,
\end{align*}
where $C$ is an arbitrary constant. Now by Fundamental Theorem of Calculus,
\begin{align*}
\int_{-1}^1 3x^2\sqrt{x^3+1}dx&=\frac{2}{3}[(x^3+1)^{\frac{3}{2}}]_{-1}^1\\
&=\frac{4\sqrt{2}}{3}.
\end{align*}
But there is a better way to do this as shown in the following theorem. Its proof is straightforward.
Theorem. If $u’$ is continuous on $[a,b]$ and $f$ is continuous on the range of $u$, then
$$\int_a^bf(u(x))u'(x)dx=\int_{u(a)}^{u(b)}f(u)du.$$
Example. Let us replay the previous example using this theorem. Again let $u=x^3+1$. Then $du=3x^2dx$ and $u(-1)=0$, $u(1)=2$. Now, by the above theorem,
\begin{align*}
\int_{-1}^1 3x^2\sqrt{x^3+1}dx&=\int_0^2\sqrt{u}du\\
&=\frac{2}{3}[u^{\frac{3}{2}}]_0^2\\
&=\frac{4\sqrt{2}}{3}.
\end{align*}
I believe you will find this more simple than previous method.
Example. Evaluate $\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\cot\theta\csc^2\theta d\theta$.
Solution. Let $u=\cot\theta$. Then $u\left(\frac{\pi}{4}\right)=1$, $u\left(\frac{\pi}{2}\right)=0$, and $du=-\csc^2\theta d\theta$. Hence, \begin{align*}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\cot\theta\csc^2\theta d\theta&=-\int_1^0 udu\\&=\frac{1}{2}\end{align*}
I will finish this lecture with the following nice properties.
Theorem. Let $f$ be a continuous function on $[-a,a]$.
(a) If $f$ is an even function, then $\int_{-a}^a f(x)dx=2\int_0^a f(x)dx$.
(b) If $f$ is an odd function, then $\int_{-a}^a f(x)dx=0$.
This can be easily understood from pictures using the symmetries of even and odd functions. But the theorem can be proved using substitution. I will leave it to you.
Example. \begin{align*}\int_{-2}^2(x^4-4x^2+6)dx&=2\int_0^2(x^4-4x^2+6)dx\\&=2\left[\frac{x^5}{5}-\frac{4}{3}x^3+6x\right]_0^2\\&=\frac{232}{15}\end{align*}
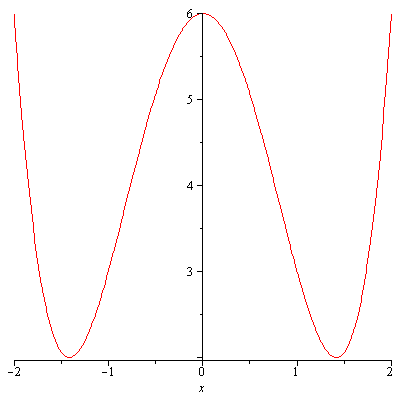
The graph of y=x^4-4x^2+6 on [-2,2].

![The graph of f(x)=3x^4-16x^3+18x^2 on [-1,4]](http://sunglee.us/mathphysarchive/wp-content/uploads/2015/10/maxmin.gif)