The derivative $\frac{d{\bf r}}{dt}={\bf r}'(t)$ of a vector-valued function ${\bf r}(t)=(x(t),y(t),z(t))$ is defined by $$\begin{equation}\label{eq:vectorderivative}\frac{d{\bf r}}{dt}=\lim_{\Delta t\to 0}\frac{{\bf r}(t+\Delta t)-{\bf r}(t)}{\Delta t}\end{equation}$$ In case of a scalar-valued function or a real-valued function, the geometric meaning of derivative is that it is the slope of tangent line. In case of a vector-valued function, the geometric meaning of derivative is that it is the tangent vector. It can be easily seen from Figure 1. As $\Delta t$ gets smaller and smaller, $\frac{{\bf r}(t+\Delta t)-{\bf r}(t)}{\Delta t}$ gets closer to a line tangent to ${\bf r}(t)$.

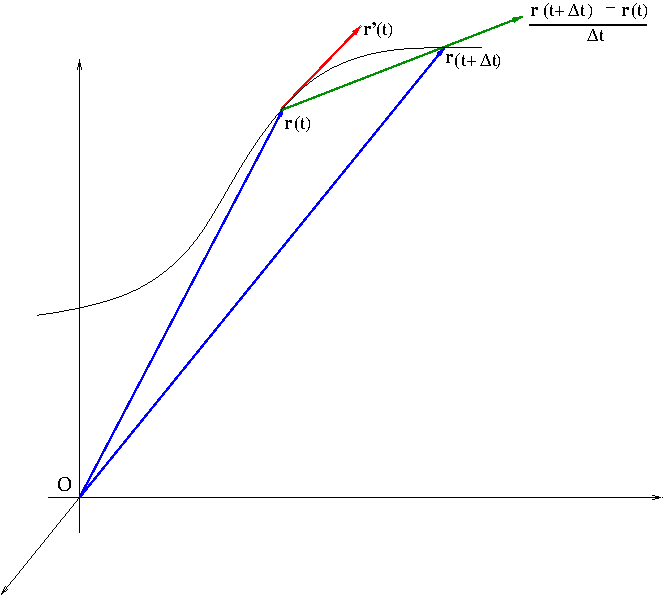
From the definition $\eqref{eq:vectorderivative}$, it is straightforward to show $$\begin{equation}\label{eq:vectorderivative2}{\bf r}'(t)=(x'(t),y'(t),z'(t))\end{equation}$$

If ${\bf r}'(t)\ne 0$, the unit tangent vector ${\bf T}(t)$ of ${\bf r}(t)$ is given by $$\begin{equation}\label{eq:unittangent}{\bf T}(t)=\frac{{\bf r}'(t)}{|{\bf r}'(t)|}\end{equation}$$

Example.

1. Find the derivative of ${\bf r}(t)=(1+t^3){\bf i}+te^{-t}{\bf j}+\sin 2t{\bf k}$.
2. Find the unit tangent vector when $t=0$.

Solution.

1. Using $\eqref{eq:vectorderivative2}$, we have $${\bf r}'(t)=3t^2{\bf i}+(1-t)e^{-t}{\bf j}+2\cos 2t{\bf k}$$
2. ${\bf r}'(0)={\bf j}+2{\bf k}$ and $|{\bf r}'(0)|=\sqrt{5}$. So by $\eqref{eq:unittangent}$, we have $${\bf T}(0)=\frac{{\bf r}'(0)}{|{\bf r}'(0)|}=\frac{1}{\sqrt{5}}{\bf j}+\frac{2}{\sqrt{5}}{\bf k}$$

The following theorem is a summary of differentiation rules for vector-valued functions. We omit the proofs of these rules. They can be proved straightforwardly from differentiation rules for real-valued functions. Note that there are three different types of the product rule or the Leibniz rule for vector-valued functions (rules 3, 4, and 5).

Theorem. Let ${\bf u}(t)$ and ${\bf v}(t)$ be differentiable vector-valued functions, $f(t)$ a scalar function, and $c$ a scalar. Then

1. $\frac{d}{t}[{\bf u}(t)+{\bf v}(t)]={\bf u}'(t)+{\bf v}'(t)$
2. $\frac{d}{dt}[c{\bf u}(t)]=c{\bf u}'(t)$
3. $\frac{d}{dt}[f(t){\bf u}(t)]=f'(t){\bf u}(t)+f(t){\bf u}'(t)$
4. $\frac{d}{dt}[{\bf u}(t)\cdot{\bf v}(t)]={\bf u}'(t)\cdot{\bf v}(t)+{\bf u}(t)\cdot{\bf v}'(t)$
5. $\frac{d}{dt}[{\bf u}(t)\times{\bf v}(t)]={\bf u}'(t)\times{\bf v}(t)+{\bf u}(t)\times{\bf v}'(t)$
6. $\frac{d}{dt}[{\bf u}(f(t))]=f'(t){\bf u}'(f(t))$ (Chain Rule)

Example. Show that if $|{\bf r}(t)|=c$ (a constant), then ${\bf r}'(t)$ is orthogonal to ${\bf r}(t)$ for all $t$.

Proof. Differentiating ${\bf r}(t)\cdot{\bf r}(t)=|{\bf r}(t)|^2=c^2$ using the Leibniz rule 5, we obtain $$0=\frac{d}{dt}[{\bf r}(t)\cdot{\bf r}(t)]={\bf r}'(t){\bf r}(t)+{\bf r}(t){\bf r}'(t)=2{\bf r}'(t)\cdot{\bf r}(t)$$ This implies that ${\bf r}'(t)$ is orthogonal to ${\bf r}(t)$.

As seen in $\eqref{eq:vectorderivative2}$, the derivative of a vector-valued functions is obtained by differentiating component-wise. The indefinite and definite integral of a vector-valued function are done similarly by integrating component-wise, namely $$\begin{equation}\label{eq:vectorintegral}\int{\bf r}(t)dt=\left(\int x(t)dt\right){\bf i}+\left(\int y(t)dt\right){\bf j}+\left(\int z(t)dt\right){\bf k}\end{equation}$$ and $$\begin{equation}\label{eq:vectorintegral2}\int_a^b{\bf r}(t)dt=\left(\int_a^b x(t)dt\right){\bf i}+\left(\int_a^b y(t)dt\right){\bf j}+\left(\int_a^b z(t)dt\right){\bf k}\end{equation}$$ , respectively. When evaluate the definite integral of a vector-valued function, one can use $\eqref{eq:vectorintegral2}$ but it would be easier to first find the indefinite integral using $\eqref{eq:vectorintegral}$ and then evaluate the definite integral the Fundamental Theorem of Calculus (and yes, the Fundamental Theorem of Calculus still works for vector-valued functions).

Example. Find $\int_0^{\frac{\pi}{2}}{\bf r}(t)dt$ if ${\bf r}(t)=2\cos t{\bf i}+\sin t{\bf j}+2t{\bf k}$.

Solution. $$\begin{align*}\int{\bf r}(t)dt&=\left(\int 2\cos tdt\right){\bf i}+\left(\int \sin tdt\right){\bf j}+\left(\int 2tdt\right){\bf k}\\&=2\sin t{\bf i}-\cos t{\bf j}+t^2{\bf k}+{\bf C}\end{align*}$$ where ${\bf C}$ is a vector-valued constant of integration. Now, $$\int_0^{\frac{\pi}{2}}{\bf r}(t)dt=[2\sin t{\bf i}-\cos t{\bf j}+t^2{\bf k}]_0^{\frac{\pi}{2}}=2{\bf i}+{\bf j}+\frac{\pi^2}{4}{\bf k}$$

Examples in this note have been taken from [1].

References.

[1] Calculus, Early Transcendentals, James Stewart, 6th Edition, Thompson Brooks/Cole