You remember from algebra that a line in the plane can be determined by its slope and a point on the line or two points on the line (in which case those two points determine the slope). For a space line, slope is not a suitable ingredient. It’s alternative ingredient is a vector parallel to the line. As shown in Figure 1, with a point ${\bf r}_0=(x_0,y_0,z_0)$ on the line $L$ and a vector ${\bf v}=(a,b,c)$ parallel to $L$, we can determine any point ${\bf r}=(x,y,z)$ on $L$ by vector addition of ${\bf r}_0$ and $t{\bf v}$, a dilation of ${\bf v}$: \begin{equation}\label{eq:spaceline}{\bf r}={\bf r}_0+t{\bf v}\end{equation} where $-\infty<t<\infty$. The equation \eqref{eq:spaceline} is called a vector equation of $L$.

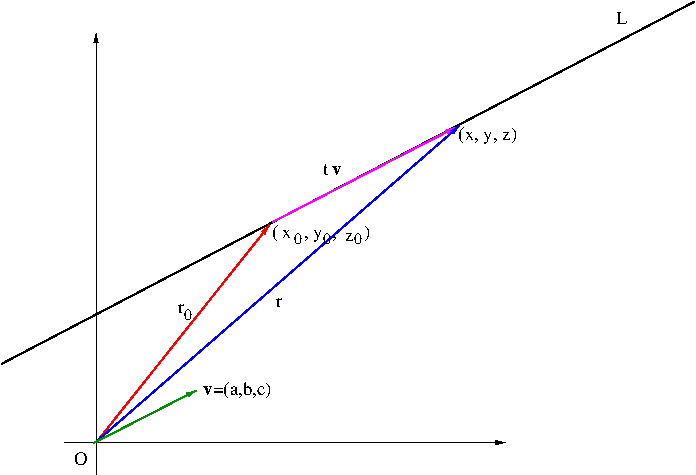
In terms of the components, \eqref{eq:spaceline} can be written as \begin{equation}\begin{aligned}x&=x_0+at\\y&=y_0+bt\\z&=z_0+ct\end{aligned}\label{eq:spaceline2}\end{equation} where $-\infty<t<\infty$. The equations in \eqref{eq:spaceline2} are called parametric equations of $L$. Solving the parametric equations in \eqref{eq:spaceline2} for $t$, we also obtain \begin{equation}\label{eq:spaceline3}\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\end{equation} The equations in \eqref{eq:spaceline3} are called symmetric equations of $L$. Often we need to work with a line segment. The vector equation \eqref{eq:spaceline} can be used to figure out an equation of a line segment. Consider the line segment from ${\bf r}_0$ to ${\bf r}_1$. Then the difference ${\bf r}_1-{\bf r}_0$ is a vector parallel to the line segment and by \eqref{eq:spaceline}, we have \begin{align*}{\bf r}(t)&={\bf r}_0+t({\bf r}_1-{\bf r}_0)\\&=(1-t){\bf r}_0+t{\bf r}_1\end{align*} This still represents an infinite line through ${\bf r}_0$ and ${\bf r}_1$. By limiting the range of $t$ to represent only the line segment from ${\bf r}_0$ to ${\bf r}_1$, we obtain an equation of the line segment \begin{equation}\label{eq:linesegment}{\bf r}(t)=(1-t){\bf r}_0+t{\bf r}_1\end{equation} where $0\leq t\leq 1$.

Example.

1. Find a vector equation and parametric equations for the line that passes through the point $(5,1,3)$ and is parallel to the vector ${\bf i}+4{\bf j}-2{\bf k}$.
2. Find two other points on the line.

Solution.

1. ${\bf r}_0=(5,1,3)$ and ${\bf v}=(1,4,-2)$. Hence by \eqref{eq:spaceline}, we have $${\bf r}(t)=(5,1,3)+t(1,4,-2)=(5+t,1+4t,3-2t)$$ Parametric equations are $$x(t)=5+t,\ y(t)=1+4t,\ z(t)=3-2t$$
2. From the parametric equations, for example, $t=1$ gives $(6,5,1)$ and $t=-1$ gives $(4,-3,5)$.

Example.

1. Find parametric equations and symmetric equations of the line that passes through the points $A(2,4,-3)$ and $B(3,-1,1)$.
2. At what point does this line intersect the $xy$-plane?

Solution.

1. Note that the vector ${\bf v}=\overrightarrow{AB}=(1, -5, 4)$ is parallel to the line. So $a=1$, $b=-5$, and $c=4$. By taking ${\bf r}_0=(x_0,y_0,z_0)=(2,4,-3)$, we have the parametric equations $$x=2+t,\ y=4-5t,\ z=-3+4t$$ Symmetric equations are then $$\frac{x-2}{1}=\frac{y-4}{-5}=\frac{z+3}{4}$$
2. The line intersects the $xy$-plane when $z=0$. By setting $z=0$ in the symmetric equations from part 1, we get $$\frac{x-2}{1}=\frac{y-4}{-5}=\frac{3}{4}$$ Solving these equations for $x$ and $y$ respectively, we find $x=\frac{11}{4}$ and $y=\frac{1}{4}$.

As we have seen, a line is determined by a point on the line and a vector parallel to the line. A plane, on the other hand, can be determined by a point ${\bf r}_0$ on the plane and a vector ${\bf n}$ perpendicular to the plane (such a vector is called a normal vector to the plane). See Figure 2.

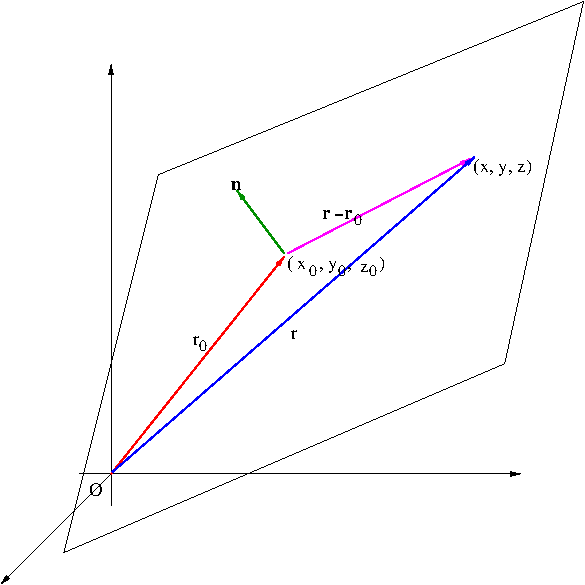
From Figure 2, we see that \begin{equation}\label{eq:plane}{\bf n}\cdot({\bf r}-{\bf r}_0)=0\end{equation} The equation \eqref{eq:plane} is called a vector equation of the plane. If ${\bf n}=(a,b,c)$, ${\bf r}=(x,y,z)$, and ${\bf r}_0=(x_0,y_0,z_0)$, then the equation \eqref{eq:plane} can be written as \begin{equation}\label{eq:plane2}a(x-x_0)+b(y-y_0)+c(z-z_0)=0\end{equation}

Example. Find an equation of the plane through the point $(2,4,-1)$ with normal vector ${\bf n}=(2,3,4)$. Find the intercepts and sketch the plane.

Solution. $a=2$, $b=3$, $c=4$, $x_0=2$, $y_0=4$, and $z_0=-1$. So by the equation \eqref{eq:plane2}, we have $$2(x-2)+3(y-4)+4(z+1)=0$$ or $$2x+3y+4z=12$$ To find the $x$-intercept, set $y=z=0$ in the equation and we get $x=6$. Similarly, we find the $y$- and $z$-intercepts $y=4$ and $z=3$, respectively. Figure 3 shows the plane.

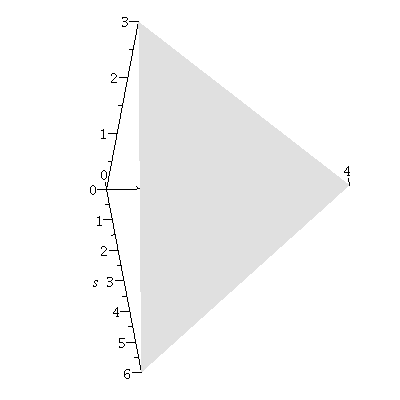
Example. Find an equation of the plane that passes through the points $P(1,3,2)$, $Q(3,-1,6)$, and $R(5,2,0)$.

Solution. The vectors $\overrightarrow{PQ}=(2,-4,4)$ and $\overrightarrow{PR}=(4,-1,-2)$ are on the plane, so the cross product $$\overrightarrow{PQ}\times\overrightarrow{PR}=\begin{vmatrix}{\bf i} & {\bf j} & {\bf k}\\2 & -4 & 4\\4 & -1 & -2\end{vmatrix}=12{\bf i}+20{\bf j}+14{\bf k}$$ is a normal vector to the plane. With $(x_0,y_0,z_0)=(1,3,2)$ and $(a,b,c)=(12,20,14)$, we find an equation of the plane $$12(x-1)+20(y-3)+14(z-2)=0$$ or $$6x+10y+7z=50$$

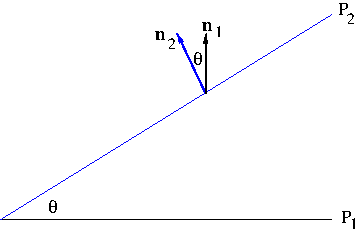
Using basic geometry, we see that the angle between two planes $P_1$ and $P_2$ is the same as the angle between their respective normal vectors ${\bf n}_1$ and ${\bf n}_2$. See Figure 4 where cross sections of two planes $P_1$ and $P_2$ are shown.

Example.

1. Find the angle between the planes $x+y+z=1$ and $x-2y+3z=1$.
2. Find the symmetric equations for the line of intersection $L$ of these two planes

Solution.

1. The normal vectors of these planes are ${\bf n}_1=(1,1,1)$ and ${\bf n}_2=(1,-2,3)$. Let $\theta$ be the angle between ${\bf n}_1$ and ${\bf n}_2$ . Then $$\cos\theta=\frac{{\bf n}_1\cdot{\bf n }_2}{|{\bf n}_1||{\bf n}_2|}=\frac{1(1)+1(-2)+1(3)}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(-2)^2+3^2}}=\frac{2}{\sqrt{42}}$$ Thus, $$\theta=\cos^{-1}\left(\frac{2}{\sqrt{42}}\right)\approx 72^\circ$$
2. First, let us find a point on $L$. Set $z=0$. Then we have $x+y=1$ and $x-2y=1$. Solving these two equations simultaneously we find $x=1$ and $y=0$. So $(1,1,0)$ is on the line $L$. Now we need a vector parallel to the line $L$. The cross product $${\bf n}_1\times{\bf n}_2=\begin{vmatrix}{\bf i} & {\bf j} & {\bf k}\\1 & 1 & 1\\1 & -2 & 3\end{vmatrix}=5{\bf i}-2{\bf j}-3{\bf k}$$ is perpendicular to both ${\bf n}_1$ and ${\bf n}_2$, hence it is parallel to $L$. Therefore, the symmetric equations of $L$ are $$\frac{x-1}{5}=\frac{y}{-5}=\frac{z}{-3}$$

Let us find the distance $D$ from a point $Q(x_1,y_1,z_1)$ to the plane $ax+by+cz+d=0$. See Figure 5.

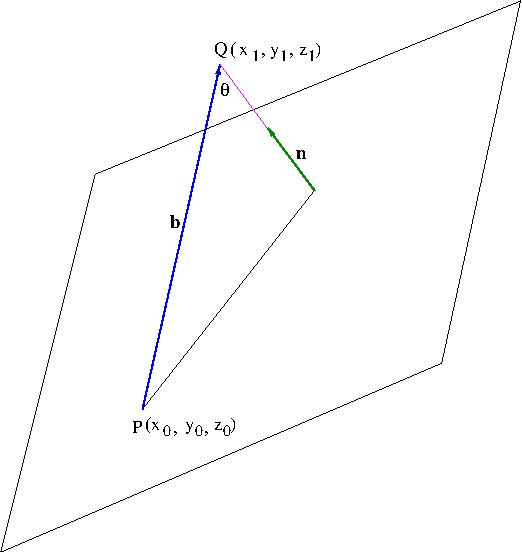
Let $P(x_0,y_0,z_0)$ be a point in the plane and let ${\bf b}=\overrightarrow{PQ}=(x_1-x_0,y_1-y_0,z_1-z_0)$. Then from Figure 5, we see that the distance from $Q$ to the plane is given by the scalar projection of ${\bf b}$ onto the normal vector ${\bf n}$: \begin{align*}D&=|\mathrm{comp}_{\bf n}{\bf b}|=\frac{|{\bf b}\cdot{\bf n}|}{|{\bf n}|}\\&=\frac{|a(x_1-x_0)+b(y_1-y_0)+c(z_1-z_0)|}{\sqrt{a^2+b^2+c^2}}\\&=\frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}\end{align*} The last expression is obtained by the fact that $ax_0+by_0+cz_0=-d$. Therefore, the distance $D$ from a point $Q(x_1,y_1,z_1)$ to the plane $ax+by+cz+d=0$ is \begin{equation}\label{eq:distance2plane}D=\frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}\end{equation}

Example. Find the distance between the parallel planes $10x+2y-2z=5$ and $5x+y-z=1$.

Solution. One can easily see that the two planes are parallel because their respective normal vectors $(10,2,-2)$ and $(5,1,-1)$ are parallel. To find the distance between the planes, first one will have to find a point in one plane and then use the formula \eqref{eq:distance2plane} to find the distance. Let us find a point in the plane $10x+2y-2z=5$. One can, for instance, use the $x$-intercept, so let $y=z=0$. Then $10x=5$ i.e. $x=\frac{1}{2}$. The distance from $\left(\frac{1}{2},0,0\right)$ to the plane $5x+y-z=1$ is $$D=\frac{\left|5\left(\frac{1}{2}\right)+1(0)-(0)\right|}{\sqrt{5^2+1^2+(-1)^2}}=\frac{\sqrt{3}}{6}$$

Examples in this note have been taken from [1].

References.

[1] Calculus, Early Transcendentals, James Stewart, 6th Edition, Thompson Brooks/Cole