We have already discussed the length of a plane curve represented by the parametric equation ${\bf r}(t)=(x(t),y(t))$, $a\leq t\leq b$ here. The same goes for a space curve. Namely, if ${\bf r}(t)=(x(t),y(t),z(t))$, $a\leq t\leq b$, then its arc length $L$ is given by \begin{equation}\begin{aligned}L&=\int_a^b|{\bf r}'(t)|dt\\&=\int_a^b\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2}dt\end{aligned}\label{eq:spacearclength}\end{equation}
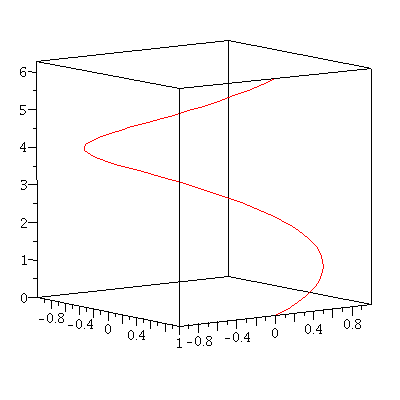
Example. Find the length of the arc of the circular helix $${\bf r}(t)=\cos t{\bf i}+\sin t{\bf j}+t{\bf k}$$ from the point $(1,0,0)$ to the point $(1,0,2\pi)$.
Solution. ${\bf r}'(t)=-\sin t{\bf i}+\cos t{\bf j}+{\bf k}$ so we have $$|{\bf r}'(t)|=\sqrt{(-\sin t)^2+(\cos t)^2+1^2}=\sqrt{2}$$ The arc is going from $(1,0,0)$ to $(1,0,2\pi)$ and the $z$-component of ${\bf r}(t)$ is $t$, so $0\leq t\leq 2\pi$. Now, using \eqref{eq:spacearclength}, we obtain $$L=\int_0^{2\pi}|{\bf r}'(t)|dt=\int_0^{2\pi}\sqrt{2}dt=2\sqrt{2}\pi$$ Figure 1 shows the circular helix from $t=0$ to $t=2\pi$.
Given a curve ${\bf r}(t)$, $a\leq t\leq b$, sometimes we need to reparametrize it by another parameter $s$ for various reasons. Imagine that the curve represents the path of a particle moving in space. A reparametrization does not change the path of the particle (hence nor the distance it traveled) but it changes the particle’s speed! To see this, let $t=t(s)$, $\alpha\leq s\leq\beta$, $a=t(\alpha)$, $b=t(\beta)$ be an increasing and differentiable function. Since $t=t(s)$ is one-to-one and onto, ${\bf r}(t)$ and ${\bf r}(t(s))$, its reparametrization by the parameter $s$, represent the same path. By the chain rule, \begin{equation}\label{eq:reparametrization}\frac{d}{ds}{\bf r}(t(s))=\frac{d}{dt}{\bf r}(t)\frac{dt}{ds}\end{equation} Thus we see that the speed of the reparametrization $\left|{\bf r}(t(s))\right|$ differs from that of ${\bf r}(t)$ by a factor of $\left|\frac{dt}{ds}\right|=\frac{dt}{ds}$ (since $\frac{dt}{ds}>0$). However, the arc length of the reparametrization is \begin{align*}\int_{\alpha}^{\beta}\left|\frac{d}{ds}{\bf r}(t(s))\right|ds&=\int_{\alpha}^{\beta}\left|\frac{d}{dt}{\bf r}(t)\right|\frac{dt}{ds}ds\\&=\int_a^b\left|\frac{d}{dt}{\bf r}(t)\right|dt=L\end{align*} That is, no change of the distance.
There is a particular reparametrization we are interested. To discuss that, suppose ${\bf r}(t)$, $a\leq t\leq b$ be a differentiable curve in space such that ${\bf r}'(t)\ne 0$ for all $t$. Such a curve is said to be regular or smooth. Let us now define the arc length function \begin{equation}\label{eq:arclengthfunction}s(t)=\int_a^t|{\bf r}'(u)|du\end{equation} By the Fundamental Theorem of Calculus, we have \begin{equation}\label{eq:arclengthfunction2}\frac{ds}{dt}=|{\bf r}'(t)|>0\end{equation} and so the arc length function $s=s(t)$ is increasing. This means that $s(t)$ is one-to-one and onto, so it is invertible. It’s inverse function can be written as $t=t(s)$ and ${\bf r}(t(s))$ is called the reparamerization by arc length. The reason we are interested in this particular reparametrization is that it results in the unit speed: From \eqref{eq:reparametrization} and \eqref{eq:arclengthfunction2}, $$\left|\frac{d}{ds}{\bf r}(t(s))\right|=|{\bf r}'(t)|\left|\frac{dt}{ds}\right|=|{\bf r}'(t)|\frac{1}{|{\bf r}'(t)|}=1$$ So it is also called the unit-speed reparametrization. The reparametrization by arc length plays an important role in defining the curvature of a curve. This will be discussed elsewhere.
Example. Reparametrize the helix ${\bf r}(t)=\cos t{\bf i}+\sin t{\bf j}+t{\bf k}$ by arc length measured from $(1,0,0)$in the direction of increasing $t$.
Solution. The initial point $(1,0,0)$ corresponds to $t=0$. From the previous example, we know that the helix has the constant speed $|{\bf r}'(t)|=\sqrt{2}$. Thus, $$s(t)=\int_0^t|{\bf r}'(u)|du=\sqrt{2}t$$ Hence, we obtain $t=\frac{s}{\sqrt{2}}$. The reparametrization is then given by $${\bf r}(t(s))=\cos\left(\frac{s}{\sqrt{2}}\right){\bf i}+\sin\left(\frac{s}{\sqrt{2}}\right){\bf j}+\frac{s}{\sqrt{2}}{\bf k}$$
Examples in this note have been taken from [1].
References.
[1] Calculus, Early Transcendentals, James Stewart, 6th Edition, Thompson Brooks/Cole
