Definition. Let $A$ be a nonempty set. Then $R\subseteq A\times A$ is called a binary relation on $A$. A binary relation $R$ on $A$ is said to be an equivalence relation if

1. $R$ is reflexive: $\forall x\in A$, $(x,x)\in R$
2. $R$ is symmetric: $(x,y)\in R\Longrightarrow (y,x)\in R$
3. $R$ is transitive: $(x,y)\in R\ \mathrm{and}\ (y,z)\in R\Longrightarrow (x,z)\in R$

Definition. Let $R$ be an equivalence relation on a set $A$. For each $x\in A$, let $$[x]=\{y\in A: (y,x)\in R\}$$ Then $[x]$ is called the ($R$-)equivalence class of $x\in A$.

Theorem 1. Let $R$ be an equivalence relation on a set $A$. Then

1. $\forall x,y\in A$, $[x]\cap [y]=\emptyset$ or $[x]=[y]$.
2. $A=\bigcup_{x\in A}[x]$.

Proof.

1. Let $x,y\in A$. If $[x]\cap [y]=\emptyset$, then we are done. Now suppose that $[x]\cap [y]\ne\emptyset$. Then $\exists z\in[x]\cap [y]$ so that \begin{align*}(z,x)\in R\ \mathrm{and}\ (z,y)\in R&\Longrightarrow (x,z)\in R\ \mathrm{and}\ (z,y)\in R\\&\Longrightarrow (x,y)\in R\end{align*} This implies that $[x]=[y]$.
2. Left as an exercise.

Definition. Let $A$ be a set. By a partition of $A$ we mean a family $\{A_i\}_{i\in I}$of nonempty subsets of $A$ such that

1. $\forall i,j\in I$, $A_i\cap A_j=\emptyset$ or $A_i=A_j$.
2. $A=\bigcup_{i\in I}A_i$

Theorem 1 says that given an equivalence relation $R$ on $A$, the $R$-equivalence classes form a partition of $A$. Conversely, given a partition $\{A_i\}_{i\in I}$, one can define an equivalence relation $R$ whose equivalence classes coincide with the $A_i$´s.

Theorem 2. Let $\{A_i\}_{i\in I}$ be a partition of a set $A$. Define a relation $R$ on $A$ as follows: $$\forall x,y\in A,\ (x,y)\in R\Longleftrightarrow x,y\in A_i\ \mbox{for some}\ i\in I$$ Then $R$ is an equivalence relation on $A$ and the $R$-equivalence classes coincide with the $A_i$´s.

Proof. Left as an exercise.

Given an equivalence relation $R$ on a set $A$, the set of all equivalence classes is called the quotient set of $A$ modulo (or mod in short) $R$ and is denoted by $A/R$ i.e. $$A/R=\{[x]: x\in A\}$$

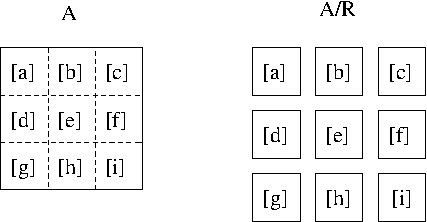
There is a map $\gamma: A\longrightarrow A/R$ defined by $$\forall x\in A,\ \gamma(x)=[x]$$ $\gamma$ is called the canonical map from $A$ to $A/R$.

Example 1. (The Vector Space $\mathbb{R}^3$) Let $V$ be the set of all directed arrows in 3-space $\mathbb{R}^3$. Define a relation $\equiv$ on $V$ as follows: $$\forall \overrightarrow{AB},\overrightarrow{CD}\in V,\ \overrightarrow{AB}\equiv\overrightarrow{CD}\Longleftrightarrow\ \overrightarrow{AB}\ \mathrm{and}\ \overrightarrow{CD}\ \mbox{have the same direction and magnitude}$$ Then clearly $\equiv$ is an equivalence relation on $V$. Denote by $\mathcal{V}$ the quotient set $V/\equiv$ and each equivalence class $[\overrightarrow{AB}]\in\mathcal{V}$ is called a vector. Each directed arrow $\overrightarrow{AB}$ whose starting point is $A$ and terminal point is $B$ is $\equiv$-related to a directed arrow $\vec{a}$ whose starting point is the origin $O=(0,0,0)$ and terminal point is $B-A$. $\vec{a}$ can be identified with its terminal point $B-A$ which is an ordered triple $(a_1,a_2,a_3)$. Hence from here on, without loss of generality, we may assume that each equivalence class is represented by such a vector. Define the vector addition $+:\mathcal{V}\times\mathcal{V}\longrightarrow\mathcal{V}$ by $$\forall [\vec{a}],[\vec{b}]\in\mathcal{V},\ [\vec{a}]+[\vec{b}]:=[\vec{a}+\vec{b}]$$ Here, $$\vec{a}+\vec{b}=(a_1,a_2,a_3)+(b_1,b_2,b_3)=(a_1+b_1,a_2+b_2,a_3+b_3)$$ Also define the scalar multiplication $\cdot :\mathbb{R}\times\mathcal{V}\longrightarrow\mathcal{V}$ by $$\forall c\in\mathbb{R},\ \forall [\vec{a}]\in\mathbb{V},\ c[\vec{a}]:=[c\vec{a}]$$ Here, $$c\vec{a}=(ca_1,ca_2,ca_3)$$ Let $[\vec{a}]=[\vec{a}’]$ and $[\vec{b}]=[\vec{b}’]$. Then $\vec{a}=\vec{a}’$ and $\vec{b}=\vec{b}’$ i.e. $a_i=a’_i$ and $b_i=b’_i$, $i=1,2,3$. Thus $$\vec{a}+\vec{b}=\vec{a}’+\vec{b}’\Longrightarrow [\vec{a}]+[\vec{b}]=[\vec{a}+\vec{b}]=[\vec{a}’+\vec{b}’]=[\vec{a}’]+[\vec{b}’]$$ Hence, the vector addition is well-defined. It can be shown similarly that the scalar multiplication is also well-defined. We will see in the next example that there is a bijective from $\mathcal{V}$ to $\mathbb{R}^3$.

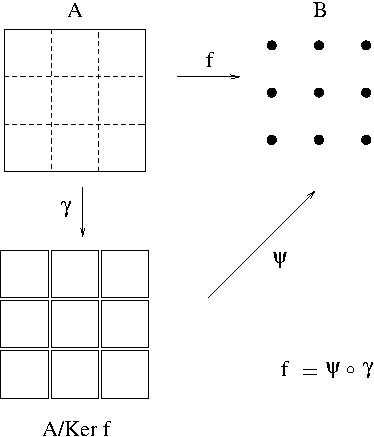
Example 2. (The Kernel of a Function) Let $f: A\longrightarrow B$ be a function. The kernel of $f$, $\ker f$ is defined by $$\ker f=\{(x,y)\in A\times A: f(x)=f(y)\}$$ It is easy to see that $\ker f$ is an equivalence relation on $A$. It turns out that the quotient set $A/\ker f$ coincides with the partition of $A$ by the pre-images $f^{-1}(z)$, $\forall z\in A$. (See Problem Set 12 #5 (b).) Now we suppose that $f: A\longrightarrow B$ is surjective (onto). Define a map $\psi: A/\ker f\longrightarrow B$ by $$\forall [x]\in A/R,\ \psi([x])=f(x)$$ Then $\psi$ is a bijective and $\gamma=\psi\circ f$, where $\gamma: A\longrightarrow A/\ker f$ is the canonical map. (Its proof is left as an exercise.)

In Example 1, we have seen that given a directed arrow $\overrightarrow{AB}$ there is a $\equiv$-related directed arrow whose starting point the origin $O$ and terminal point $B-A$ and that such a directed arrow can be identified with its terminal point $\vec{a}:=B-A=(a_1,a_2,a_3)\in\mathbb{R}^3$. This defines a surjective map $f: V\longrightarrow\mathbb{R}^3$ and $\ker f=\equiv$. Therefore, we see that there is a bijective $\psi$ from $V/\ker f=V/\equiv$ to $\mathbb{R}^3$ defined by $$\forall [\vec{a}]\in V/\equiv,\ \psi([\vec{a}])=(a_1,a_2,a_3)$$ Furthermore, this bijective is a vector space homomorphism i.e. it preserves the vector addition and the scalar multiplication: \begin{align*}\psi([\vec{a}]+[\vec{b}])&=\psi([\vec{a}])+\psi([\vec{b}])\\\psi(c[\vec{a}])&=c\psi([\vec{a}])\end{align*} Therefore $V/\equiv$ is isomorphic to $\mathbb{R}^3$ as a vector space.

Example 3. (The Construction of Rational Numbers From Integers) Let $\mathbb{Z}$ be the set of all integers. Define a relation $\sim$ on $\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})$ by $$\forall (a,b),(c,d)\in \mathbb{Z}\times(\mathbb{Z}\setminus\{0\}),\ (a,b)\sim (c,d)\Longleftrightarrow ad=bc$$ Then $\sim$ is an equivalence relation. (Its proof is left as an exercise.) The equivalence class of $(a,b)$ is denoted by $\frac{a}{b}$. For example, $(1,2)\sim (2,4)$ thus $\frac{1}{2}=\frac{2}{4}$. We see that the quotient set $\mathbb{Z}\times(\mathbb{Z}\setminus\{0\})/\sim$ can be identified with $\mathbb{Q}$, the set of all rational numbers.

Example 4. (Residue Classes Modulo $n$) Let $\mathbb{Z}$ be the set of all integers. Define a relation $\equiv\ \mathrm{mod}\ n$ on $\mathbb{Z}$ by $$\forall p,q\in\mathbb{Z},\ p\equiv q\ \mathrm{mod}\ n\Longleftrightarrow n|(p-q)$$ Then $\equiv\ \mathrm{mod}\ n$ is an equivalence relation. (Its proof is left as an exercise.) An integer $m$ can be written as $m=nk+r$ where $k$ is the quotient and $0\leq r<n$ is the remainder when $m$ is divided by $n$. Thus $m\equiv\ \mathrm{mod}\ n r$. This means that there are exactly $n-1$ equivalence classes $$[0],[1],\cdots,[n-1]$$ These equivalence classes are called the residue classes modulo $n$. The quotient set $\mathbb{Z}/\equiv\ \mathrm{mod}\ n$ is usually denoted by $\mathbb{Z}_n$. We can define addition and multiplication on $\mathbb{Z}_n$ as follows: $\forall [a],[b]\in\mathbb{Z}_n$, \begin{align*}[a]+[b]&=[a+b]\\ [a]\cdot [b]&=[ab]\end{align*} These operations are well-defined because the equivalence relation $\equiv\ \mathrm{mod}\ n$ preserves the operations, namely if $a\equiv b\ \mathrm{mod}\ n$ and $c\equiv d \mathrm{mod}\ n$ then \begin{align*}a+c&\equiv b+d\ \mathrm{mod}\ n\\ ac&\equiv bd\ \mathrm{mod}\ n\end{align*} An equivalence which preserves operations are called a congruence relation. Congruence relations play a crucial role in constructing quotient algebras. For more details about congruence relations, see for example the reference [3]. Note that the equivalence relations in Examples 1 and 3 are also congruence relations. $(\mathbb{Z}_n,+)$ is an abelian group and $(\mathbb{Z}_n,+,\cdot)$ is a commutative ring with unity. $(\mathbb{Z},+,\cdot)$ is a field if $n$ is a prime.

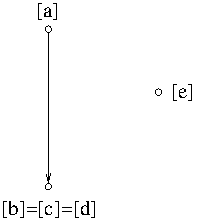
Example. (Digraphs) Let $G=(V,A)$ be a digraph. Let $\sim$ be mutual reachability relation on $V$, i.e. $\forall x,y\in V$, $x\sim y$ if and only if $x$ and $y$ are mutually reachable. It can be easily seen that mutual reachability relation is an equivalence relation. The equivalence classes are called the strongly connected components or simply strong components of the digraph $G$ and they are subgraphs of $G$.

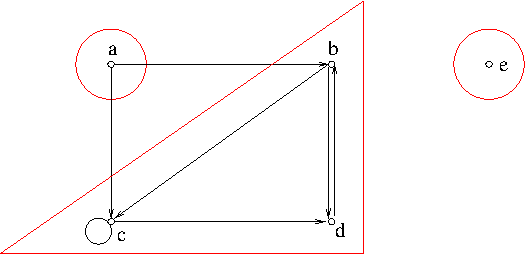
Theorem. Let $G=(V,A)$ be a digraph and let $T$ be the partition of $V$ into the strong components of $G$. Construct a new digraph $G’=(T,A’)$, where $\forall X,Y\in T$, $X\to Y\in A’$ if and only if $X\ne Y$ and $x\to y\in A$ for some $x\in X$ and $y\in Y$. Then $G’$ is a DAG.

Proof. Suppose that there is a cycle in $G’$, $x_0\to x_1\to\cdots x_k\to x_0$ for some $x_0,\cdots,x_k$ belonging to different strong components of $G$. But all theses vertices are mutually reachable in $G$ so this is a contradiction. Therefore $G’$ is acyclic.

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019

[2] Set Theory, Charles C. Pinter, Addison Wesley Publishing Company, 1971

[3] A Course in Universal Algebra, Stanley N. Burris and H. P. Sankappanavar, Graduate Texts in Mathematics, Springer-Verlag, 1981. The book is available online for free at the first named author’s web page here.