Directed graphs represent binary relations. They can be visualized as diagrams made up of points (called vertices or nodes) and arrows (called arcs or edges). Draw an arc from a vertex $v$ to a vertex $w$ to represent that $v$ is related to $w$ i.e. the ordered pair $(v,w)$ is in the relation.
Example 1. An example of a directed graph
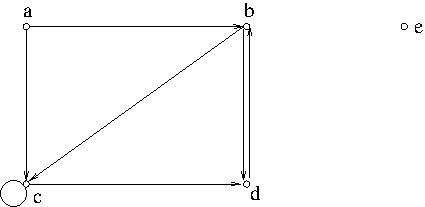
Definition. A directed graph or digraph in short is an ordered pair $(V,A)$ where $V$ is an nonempty set and $A\subseteq V\times V$ (i.e. $A$ is a binary relation on $V$). The members of $V$ are called vertices or nodes and the members of $A$ are called arcs or edges. We write arcs as $v\to w$ rather than $(v,w)$.
In Example 1, $V=\{a,b,c,d,e\}$ and \begin{align*}A&=\{(a,b), (b,c), (a,c), (c,c), (c,d), (b,d),(d,b)\}\\&=\{a\to b, b\to c, a\to c, c\to c, c\to d, b\to d, d\to b\}\end{align*}
Transportation and computer networks have natural representations of digraphs.
A walk in a digraph is a way of proceeding through a sequence of vertices by following arcs i.e. a walk in a digraph $(V,A)$ is a sequence of vertices $v_0,v_1,\cdots,v_n\in V$ for some $n\geq 0$ such that $v_i\to v_{i+1}\in A$ for each $i<n$. The length of this walk is $n$ which is the number of arcs.
Example 2. In Example 1, $b\to d$, $b\to c\to d$, $b\to c\to c\to d$, $b\to d\to b\to d$ are examples of walks from vertex $b$ to vertex $d$. The length of $b\to d$ is 1, the length of $b\to c\to d$ is 2, the length of $b\to c\to c\to d$ is 3 and the length of $b\to d\to b\to d$ is also 3. There is no walk from vertex $b$ to vertex $a$.
A path is a walk that doesn’t repeat any vertex.
Example 3. Among the walks in Example 2, $b\to d$ and $b\to c\to d$ are paths from vertex $b$ to $d$.
A walk in which the first and the last vertex are the same is called a circuit. A circuit is called a cycle if the first and the last vertices are the only repeated vertex. For example, $b\to c\to c\to b\to b$ in the digraph in Example 1 is a circuit but is not a cycle. On the other hand, $b\to c\to d\to b$ is a cycle of length 3, $b\to d\to b$ is a cycle of length 2, and $c\to c$ is a cycle of length 1.
A digraph without any cycles is said to be acyclic. The digraph in Exam 1 is not acyclic as it contains cycles.
A walk can be reduced to a path by removing nontrivial cycles. Suppose that a walk from $v$ to $w$ $$v=v_0\to\cdots\to v_n=w$$ includes a cycle $v_i\to v_{i+1}\to\cdots\to v_j$ where $i<j$ and $v_i=v_j$. Then $$v=v_0\to\cdots\to v_i\to v_{j+1}\to\cdots\to v_n=w$$ is a shorter walk from $v$ to $w$.
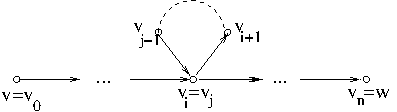
For example, the walk $b\to d\to b\to d$ in Example 1 can be reduced to the path $b\to d$ by removing the cycle $b\to d\to d$.
A vertex $w$ is said to be reachable from vertex $v$ if there is a walk or a path from $v$ to $w$. The distance from vertex $v$ to vertex $w$ in a digraph $G$, denoted by $d_G(v,w)$, is the length of the shortest path from $v$ to $w$, or is defined to be $\infty$ if there is no path from $v$ to $w$. For example, the distance from $a$ to $d$ in the digraph in Example 1 is 2 because the shortest path is $a\to c\to d$.
Lemma. The distance from one vertex of a graph to another vertex is at most the length of any walk from the first to the second.
Proof. It follows from the fact that any walk from $v$ to $w$ includes among its arcs a path from $v$ to $w$.
A digraph in which every vertex is reachable from every other vertex is said to be strongly connected.
Let $G=(V,A)$ be a digraph. Let $V’\subseteq V$ and $A’\subseteq A$. Then $(V’,A’)$ is called a subgraph of $G$. $(V,\emptyset)$ is a subgraph of $G$.
Let $G=(V,A)$ be a digraph and $V’\subset V$. Then $$(V’,\{v\to w\in A: v,w\in V’\})$$ is called the subgraph induced by $V’$.
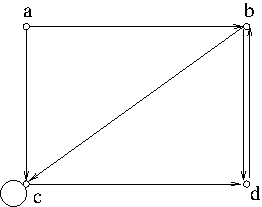
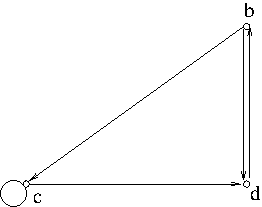
Example 4. The subgraph induced by $V\setminus\{e\}$ in Example 1 is not strongly connected. But the subgraph induced by $\{b,c,d\}$ is strongly connected.
An acyclic digraph is generally called a directed acyclic group or DAG in short.
The out-degree of a vertex is the number of arcs leaving it i.e. $|\{w\in V: v\to w\ \mbox{in}A\}|$. Similarly, the in-degree of a vertex is the number of arcs entering it.
Theorem. A finite DAG has at least one vertex of out-degree 0 and at least one vertex of in-degree 0.
Proof. Let $G=(V,A)$ be a finite DAG. Suppose that $G$ has no vertex of out-degree 0.
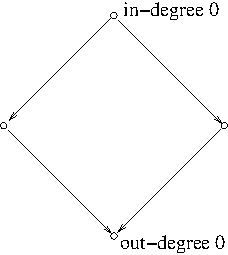
Pick a vertex $v_0$. Since $v_0$ has a positive out-degree, there exists an arc $v_0\to v_1$ for some vertex $v_1$. Since $v_1$ has a positive out-degree, there exists an arc $v_1\to v_2$ for some vertex $v_2$. One can continue doing this. But since $V$ is finite, some vertex will be repeated, creating a cycle. This is a contradiction to the graph $G$ being acyclic. A very similar argument can be made to show that $G$ has a vertex of in-degree 0.
In a DAG, a vertex of in-degree 0 is called a source and a vertex of out-degree 0 is called a sink.
A tournament graph
A tournament graph is a digraph in which every pair of distinct vertices are connected by an arc in one direction or the other, but not both. It is a natural representation of a round-robin tournament in which each players competes with all other plays in turn.
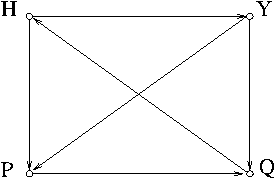
Example 5. The tournament graph in Figure 6 shows that $H$ beats both $P$ and $Y$, $Q$ beats $H$, $Y$ beats $P$, and $P$ beats $Q$. Hence we have a cycle $H\to P\to Q\to H$. Awkwardly, there is no champion!
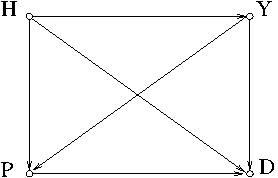
Example 6. The tournament graph in Figure 7 shows that $H$ beats $P$, $Y$, $D$, $Y$ beats $P$ and $D$, and $P$ beats $D$. Hence, $H$ is the first, $Y$ is the second, $P$ the third, and $D$ is the fourth places.
The total number of arcs in a tournament graph with $n$ vertices is $\frac{n(n-1)}{2}$, since there is exactly one arc between each pair of distinct vertices.
A linear order, denoted by $\preceq$, is a binary relation on a finite set $S=\{s_0,s_1,\cdots,s_n\}$ such that $s_i\preceq s_j$ if and only if $i\leq j$.
Example 7. Let $S=\{\mbox{all English words}\}$. Define $s_i\preceq s_j$ to mean that $s_i$ appears before $s_j$ alphabetically or they are equal. Then $\preceq$ is a linear order. This particular linear order is called the lexicographic order or the dictionary order.
A strict order of a finite set, denoted by $\prec$, is an ordering such that $s_i\prec s_j$ if and only if $i<j$.
Theorem. A tournament graph represents a strict linear order if and only if it is a DAG.
Proof. Let $G=(V,A)$ be a tournament graph. Suppose that $G$ represents a strict order. This means that the path $$v_0\to v_1\to\cdots\to v_n$$ represents $$v_0\prec v_1\prec\cdots\prec v_n$$ so every arc goes from $v_i$ to $v_j$ if $i<j$. The graph is then acyclic because any cycle will have to include at least one arc $v_j\to v_i$ where $i<j$. Conversely suppose $G$ is a DAG. We show by induction that $G$ represents a strict order. If $G$ has only one vertex, clearly $G$ represents a strict order. If $G$ has more than one vertex, at least one of the vertices, say $v_0$, has in-degree 0. Since $G$ is a tournament graph, $G$ must contain each of the arc $v_0\to v_i$ ($i\ne 0$). Consider the subgraph induced by $V\setminus\{v_0\}$. This induced subgraph is also a DAG, since all its arcs are arcs of $G$. It is also a tournament graph. The subgraph includes all the arcs of $G$ except those entering from $v_0$. By induction hypothesis, the induced subgraph represents a strict linear order $$v_1\prec v_2\prec\cdots\prec v_n$$ Since $v_0\prec v_i$ for all $i\ne 0$, we have $$v_0\prec v_1\prec\cdots\prec v_n$$ This completes the proof.
Example 8. The tournament graph in Example 7 is a DAG and it represents a strict order $H\prec Y\prec P\prec D$, while the tournament graph in Example 6 doesn’t. (It is not a DAG.)
References.
[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019
