First we begin with the Mean Value Theorem for Definite Integrals.
Theorem. If $f$ is continuous on $[a,b]$, then at some point $c\in [a,b]$,
$$f(c)(b-a)=\int_a^b f(x)dx$$
or
\begin{equation}
\label{eq:mvt}
f(c)=\frac{1}{b-a}\int_a^b f(x)dx.
\end{equation}
Notice that the RHS of \eqref{eq:mvt} is the average of $f(x)$ on $[a,b]$.
Example. Find the average value of $f(x)=4-x$ on $[0,3]$ and $c\in[0,3]$ at which $f$ actually takes on this value.
Solution. The region under $y=4-x$ on $[0,3]$ is a trapezoid and its area is $\frac{15}{2}$. So,
\begin{align*}
av(f)&=\frac{1}{3-0}\int_0^3(4-x)dx\\
&=\frac{5}{2}.
\end{align*}
Let $f(c)=\frac{5}{2}$. Then $4-c=\frac{5}{2}$ and $c=\frac{3}{2}$.
Example. Show that if $f$ is continuous on $[a,b]$ ($a\ne b$) and if $\int_a^b f(x)=0$ then $f(x)=0$ at least once in $[a,b]$.
Solution. By the MVT, there exists $c\in[a,b]$ such that
$$f(c)=\frac{1}{b-a}\int_a^b f(x)dx=0.$$
Suppose that $f(t)$ is an integrable function on a finite intervale $I$. Let $a\in I$. Then
$$F(x):=\int_a^x f(t)dt$$
defines a fuction on the interval $I$. Let $f(x)$ be a continuous function on $[a,b]$. Then
Claim 1: $F(x)=\int_a^x f(t)dt$ is continuous on $[a,b]$. (For a proof click here. For those who are not familiar with $\epsilon$-$\delta$ argument, an alternative proof is available here.)
Claim 2: $F(x)$ is differentiable on $(a,b)$ and $F'(x)=\frac{d}{dx}\int_a^xf(t)dt=f(x)$. (For a proof click here.)
The claims 1 and 2 constitute:
The Fundamental Theorem of Calculus (Part I)
If $f$ is continuous on $[a,b]$, then $F(x)=\int_a^xf(t)dt$ is continuous on $[a,b]$ and is differentiable on $(a,b)$. Moreover, $F'(x)=\frac{d}{dx}\int_a^xf(t)dt=f(x)$.
The Fundamental Theorem of Calculus (Part II) relates the definitel integral and an antiderivative of a function $f(x)$.
If $f$ is continuous on $[a,b]$ and $F$ is any antiderivative of $f$ on $[a,b]$, then
$$\int_a^b f(x)dx=F(b)-F(a).$$(For a proof click here.)
Note: The usual notation for $F(b)-F(a)$ is $F(x)|_a^b$ or $[F(x)]_a^b$.
Example. Find using the Fundamental Theorem.
- $\frac{d}{dx}\int_a^x\cos tdt$
- $\frac{d}{dx}\int_0^x\frac{1}{1+t^2}dt$
- $\frac{d}{dx}\int_x^5 3t\sin tdt$
- $\frac{d}{dx}\int_1^{x^2}\cos tdt$
Solution.
- $\frac{d}{dx}\int_a^x\cos tdt=\cos x$
- $\frac{d}{dx}\int_0^x\frac{1}{1+t^2}dt=\frac{1}{1+x^2}$
- $\frac{d}{dx}\int_x^5 3t\sin tdt=-\frac{d}{dx}\int_5^x 3t\sin tdt=-3x\sin x$
- Let $u=x^2$. Then by the chain rule, \begin{align*}\frac{d}{dx}\int_1^{x^2}\cos tdt&=\frac{d}{du}\int_1^u\cos tdt\frac{du}{dx}\\&=2x\cos x^2\end{align*}
Example. Find a function $y=f(x)$ on $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ with $\frac{dy}{dx}=\tan x$ and $f(3)=5$.
Solution. $y=\int_3^x\tan t dt+5=\ln\frac{\cos 3}{\cos x}+5$.
Example.
- $\int_0^{\pi}\cos x dx=[\sin x]_0^{\pi}=\sin\pi-\sin 0=0$.
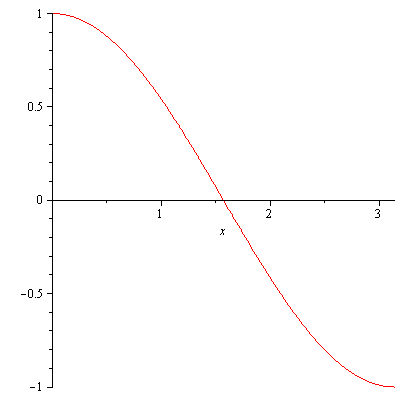
The graph of y=cos(x) on [0,pi]
- \begin{align*}\int_1^4\left(\frac{3}{2}\sqrt{x}-\frac{4}{x^2}\right)dx&=\frac{3}{2}\int_1^4 x^{\frac{1}{2}}dx-4\int_1^4x^{-2}dx\\&=[x^{\frac{3}{2}}]_1^4+4\left[\frac{1}{x}\right]_1^4\\&=4\end{align*}
Example. Find the area bounded by the $x$-axis and the parabola $y=6-x-x^2$.
Solution. Note that when you solve area problems it is extremely important to sketch the graph of the given function in order to correctly set up your integral. The reason is that some part of the function may not be nonnegative. The quadratic equation $6-x-x^2=0$ has two solutions $x=-3,2$, so these are the $x$-intercepts of the function $y=6-x-x^2$.
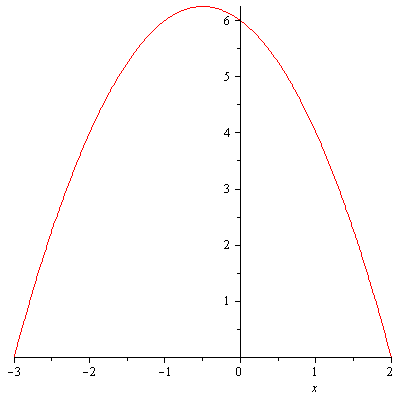
The graph of y=6-x-x^2 on [-3,2].
Example. Find the area of the region bounded by the $x$-axis and $f(x)=x^3-x^2-2x$.
Solution. The function has three $x$-intercepts $x=-1, 0, 2$. Since $f(x)$ has an odd degree and a positive leading coefficient, it’s graph is
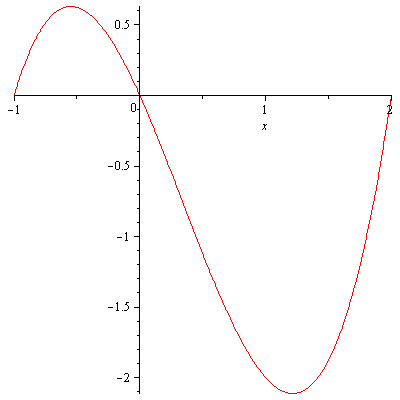
The graph of y=x^3-x^2-2x on [-1,2].

Pingback: The Substitution Rule | MathPhys Archive