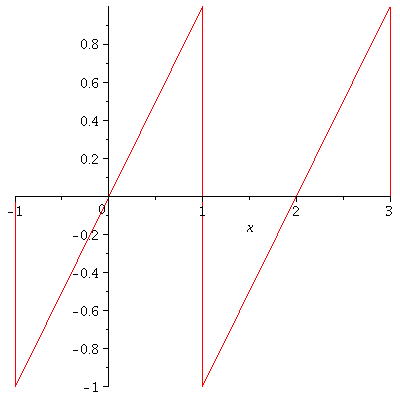d’Alembert (1717-83) studied a partial differential equation (wave equation) that describes motion of a vibrating string and Jacob Bernoulli (1654-1705) showed that its solution is represented as a trigonometric series. Fourier (1768-1830) also showed that the solution of a heat conduction problem is represented as a trigonometric series. Suppose that $f(\theta)$ satisfies $f(\theta+2\pi)=f(\theta)$ for all $\theta$. That is, $f(\theta)$ is a periodic function with period $2\pi$. Assume that $f$ is Riemann integrable on every bounded interval. Then can $f$ be expended in a series (a trigonometric series)
\begin{equation}
\label{eq:fourier}
f(\theta)=\frac{1}{2}a_0+\sum_{n=1}^\infty(a_n\cos n\theta+b_n\sin n\theta)
\end{equation}
? The answer is yes. The series \eqref{eq:fourier} can be written as
\begin{equation}
\label{eq:fourier2}
f(\theta)=\sum_{n=-\infty}^\infty c_ne^{in\theta},
\end{equation}
when $c_0=\frac{1}{2}a_0$, $c_n=\frac{1}{2}(a_n-ib_n)$, and $c_{-n}=\frac{1}{2}(a_n+ib_n)$ for $n=1,2,3,\cdots$.
\begin{align*}
\int_{-\pi}^{\pi}f(\theta)e^{-ik\theta}d\theta&=\sum_{n=-\infty}^\infty c_n\int_{-\pi}^{\pi}e^{i(n-k)\theta}d\theta\\
&=2\pi\sum_{n=-\infty}^\infty c_n\delta_{nk},
\end{align*}
where $\delta_{nk}$ denotes Kronecker’s delta. Hence we obtain
\begin{equation}
\label{eq:fc}
c_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(\theta)e^{-in\theta}d\theta,
\end{equation}
$n=1,2,3,\dots$. $a_n$ and $b_n$ are then given by
\begin{align}
\label{eq:fc2}
a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(\theta)\cos n\theta d\theta,\ n=0,1,2,\cdots,\\
\label{eq:fc3}
b_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(\theta)\sin n\theta d\theta,\ n=1,2,\cdots.
\end{align}
The series of the form \eqref{eq:fourier} or \eqref{eq:fourier2} is called a Fourier series and $c_n$ or $a_n$, $b_n$ are called the Fourier coefficients of $f$.

Lemma. If $F$ is periodic with period $P$ then $\int_a^{a+P} F(x)dx$ is independent of $a$.

Proof. Define
\begin{align*}
g(a)&:=\int_a^{a+P} F(x)dx\\
&=\int_0^{a+P}F(x)dx-\int_0^a F(x)dx.
\end{align*}
Then $g'(a)=F(a+P)-F(a)=0$ for all $a$. This means that $g$ is a constant function.

Lemma. Suppose that $f$ is periodic with period $2\pi$ and integrable on $[-\pi,\pi]$. If $f$ is even,
$$a_n=\frac{2}{\pi}\int_0^\pi f(\theta)\cos n\theta d\theta,\ b_n=0.$$
If $f$ is odd,
$$a_n=0,\ b_n=\frac{2}{\pi}\int_0^\pi f(\theta)\sin n\theta d\theta.$$

Remark. $c_0=\frac{1}{2}a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(\theta)d\theta$. Notice that this is the mean value of $f$ on $[-\pi,\pi]$.

If $f(x)$ is a periodic function with period $2L$, then it can be represented on $[-L,L]$ as
\begin{equation}
\label{eq:fourier3}
f(x)=\frac{1}{2}a_0+\sum_{n=1}^\infty\left\{a_n\cos\left(\frac{n\pi}{L}x\right)+b_n\sin\left(\frac{n\pi}{L}x\right)\right\},
\end{equation}
\begin{align}
\label{eq:fc4}
a_n&=\frac{1}{L}\int_{-L}^L f(x)\cos\left(\frac{n\pi}{L}x\right)dx,\ n=0,1,2,\cdots,\\
\label{eq:fc5}
b_n&=\frac{1}{L}\int_{-L}^L f(x)\sin\left(\frac{n\pi}{L}x\right)dx,\ n=1,2,\cdots.
\end{align}

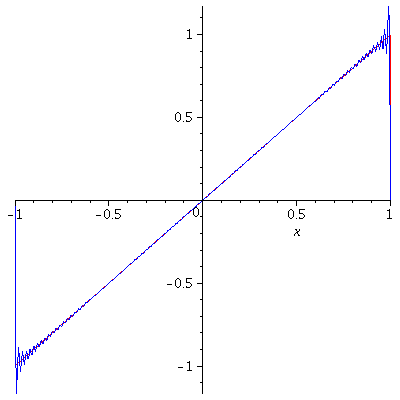
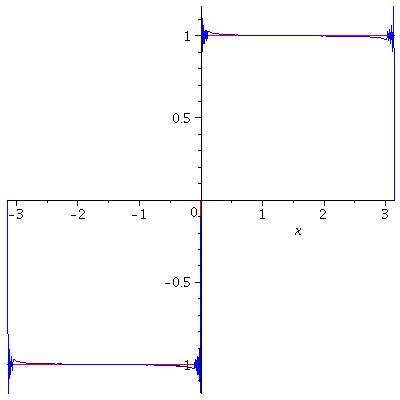
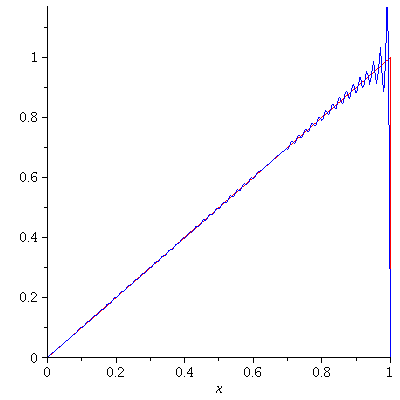
Example. [Sawtooth Function] Let $f$ be defined by
$$f(x)=x,\ -L<x<L$$
and $f(x+2L)=f(x)$.

Since $x$ is an odd function,
$$a_n=\frac{1}{L}\int_{-}^L x\cos\left(\frac{n\pi}{L}x\right)dx=0,\ n=0,1,2,\cdots.$$
For $n=1,2,\cdots$,
\begin{align*}
b_n&=\frac{1}{L}\int_{-L}^L x\sin\left(\frac{n\pi}{L}x\right)dx\\
&=\frac{2}{L}\int_0^L x\sin\left(\frac{n\pi}{L}x\right)dx\\
&=-\frac{2L(-1)^n}{n\pi}.
\end{align*}
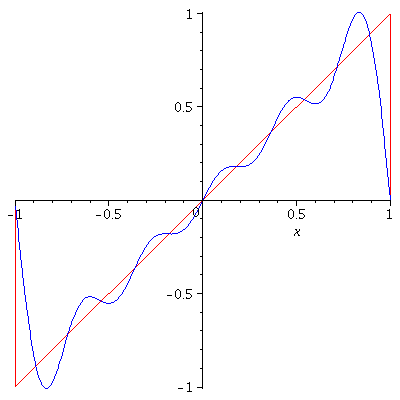
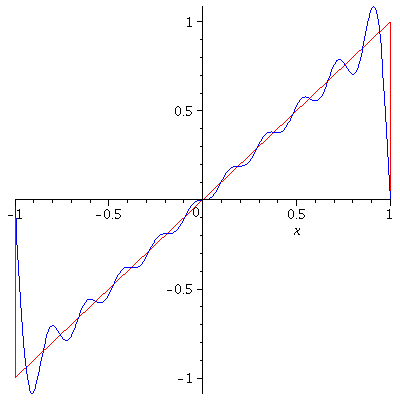
Hence, $f(x)$ is represented as the Fourier series
$$f(x)=-\frac{2L}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{n}\sin\left(\frac{n\pi}{L}x\right)$$
on the interval $[-L,L]$.

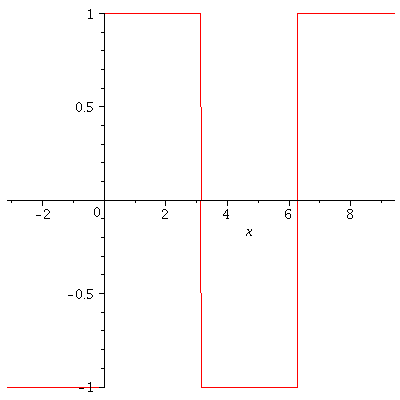
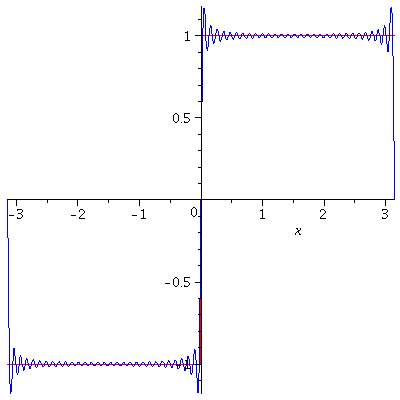
Example. [Square Wave] Let $f$ be defined by
$$f(x)=\left\{\begin{array}{ccc}
-k & \mbox{if} & -\pi<x<0\\
k & \mbox{if} & 0<x<\pi
\end{array}\right.$$
and $f(x+2\pi)=f(x)$.

The Fourier coefficients are computed to be
\begin{align*}
a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx=0,\ n=0,1,2,\cdots,\\
b_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\\
&=\frac{2k}{n\pi}[1-(-1)^n],\ n=1,2,\cdots.
\end{align*}
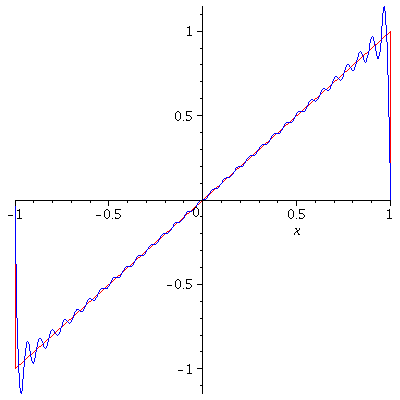
So, $b_n=0$ if $n$ is even. Now,
$$b_{2n-1}=\frac{4k}{(2n-1)\pi},\ n=1,2,\cdots$$
and
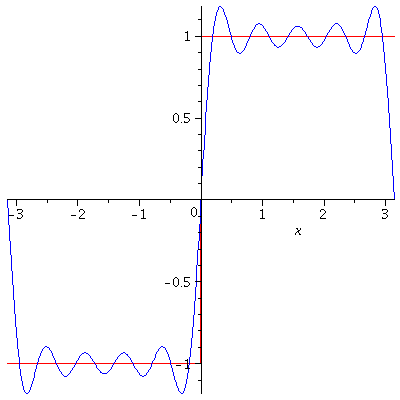
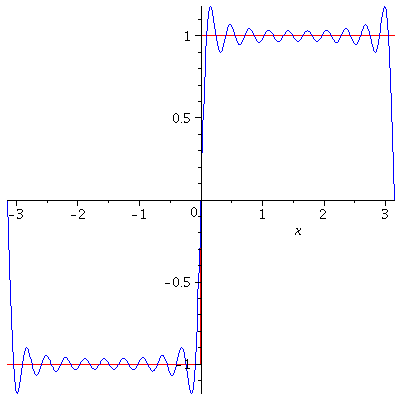
$$f(x)=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{2n-1}.$$

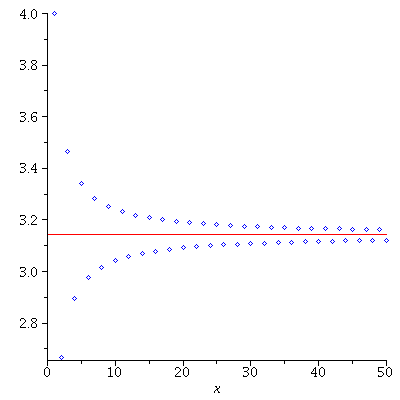
Since $0<\frac{\pi}{2}<\pi$, $f\left(\frac{\pi}{2}\right)=k$. On the other hand,
\begin{align*}
f\left(\frac{\pi}{2}\right)&=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{\sin\left(\frac{2n-1}{2}\right)\pi}{2n-1}\\
&=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{2n-1}\\
&=\frac{4k}{\pi}\left(1-\frac{1}{2}+\frac{1}{5}-\frac{1}{7}+\cdots\right).
\end{align*}
Hence, we obtain
$$\frac{\pi}{4}=1-\frac{1}{2}+\frac{1}{5}-\frac{1}{7}+\cdots$$
i.e.
$$\pi=4\sum_{n=1}^\infty\frac{(-1)^{n+1}}{2n-1}.$$
This is a famous result obtained by Gottfried Wilhelm Leibniz in 1673 from geometric considerations.

Gibbs Phenomenon

The Gibbs Phenomenon is an overshoot, a peculiarity of the Fourier series and other eigenfunction series at a simple discontinuity: the $n$th partial sum of the Fourier series has large oscillations near the jump, which may increase the maximum of the partial sum above that of the function itself. The Gibbs phenomenon is observed in the above two examples. The overshoot does not die out as the frequency increases, but approaches to a finite limit. It is a consequence of trying to approximate a discontinuous function with a finite Fourier series i.e. a partial sum of continuous functions which is always continuous.