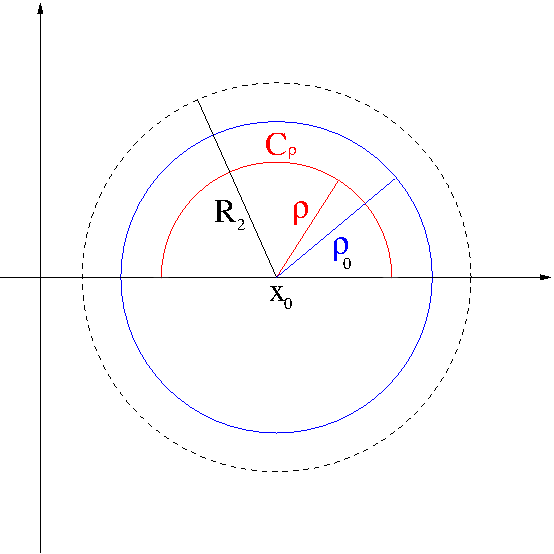
Suppose that a function $f(z)$ has a simple pole at a point $z=x_0$ on the real axis, with a Laurent series representation in a punctured disk $0<|z-x_0|<R_2$ and with residue $B_0$. Let $C_\rho$ denote the upper half of a circle $|z-x_0|=\rho$, where $\rho<R_2$ and with the clockwise direction.

$f(z)$ can be written as
$$f(z)=g(z)+\frac{B_0}{z-x_0}\ (0<|z-x_0|<R_2),$$
where $g(z)=\sum_{n=0}^\infty a_n(z-x_0)^n$. So, we have
$$\int_{C_\rho}f(z)dz=\int_{C_\rho}g(z)dz+B_0\int_{C_\rho}\frac{dz}{z-x_0}.$$
Let $\rho<\rho_0<R_2$. Then $g(z)$ is bounded on $|z-x_0|\leq\rho_0$ i.e. there exists $M>0$ such that $|g(z)|\leq M$ whenever $|z-x_0|\leq\rho_0$. Thus, we get the estimate
$$\left|\int_{C_\rho}g(z)dz\right|\leq M\pi\rho.$$
Consequently, we have
$$\lim_{\rho\to 0}\int_{C_\rho} g(z)dz=0.$$
The semi-circle $-C_\rho$ has parametric representation
$$z=x_0+\rho e^{i\theta}\ (0\leq\theta\leq\pi).$$
Using this parametric representation, we calculate
\begin{align*}
\int_{C_\rho}\frac{dz}{z-x_0}&=-\int_{-C_{\rho}}\frac{dz}{z-x_0}\\
&=-\int_0^{\pi}\frac{1}{\rho e^{i\theta}}\rho i e^{i\theta}d\theta\\
&=-\pi i.
\end{align*}
Therefore, we obtain
\begin{equation}
\label{eq:indentpath}
\lim_{\rho\to 0}\int_{C_\rho}f(z)dz=-B_0\pi i.
\end{equation}

Example. [Singularity on Contour of Integration] Evaluate the improper Integral
$$I=\int_0^\infty\frac{\sin x}{x}dx.$$

Solution. The function $f(z)=\frac{e^{iz}}{z}$ has a simple pole at $z=0$.

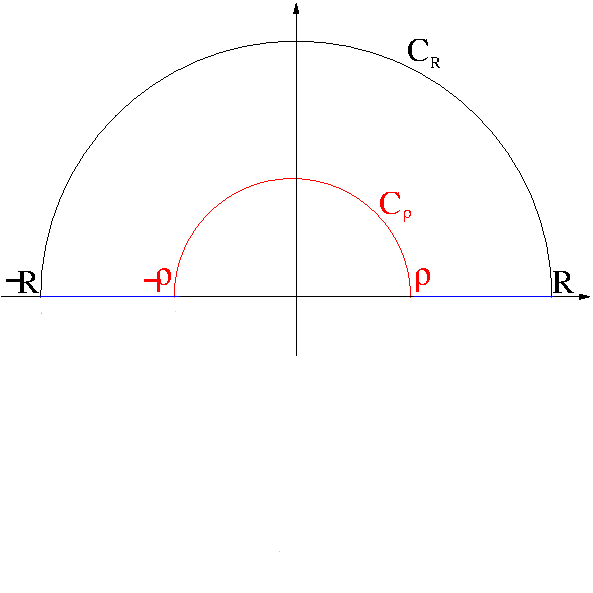Since $f(z)$ is analytic within and on the simple closed contour, we have
$$\int_{C_R} \frac{e^{iz}}{z}dz+\int_{-R}^{-\rho}\frac{e^{ix}}{x}dx+\int_{C_\rho}\frac{e^{iz}}{z}dz+\int_{\rho}^R\frac{e^{ix}}{x}dx=0.$$
Note that $\frac{1}{z}$ is analytic at all points $z$ in the upper half plane that are exterior to the circle $C_\rho$ and that for any $z$ on $C_R$, $\left|\frac{1}{z}\right|=\frac{1}{R}$
and $\lim_{R\to\infty}\frac{1}{R}=0$. Thus, by Jordan’s Lemma
$$\lim_{R\to\infty}\int_{C_R}f(z)dz=\lim_{R\to\infty}\int_{C_R}\frac{e^{iz}}{z}dz=0.$$
As $R\to\infty$ and $\rho\to 0$, we obtain
$$\int_{-\infty}^\infty\frac{e^{ix}}{x}dx=-\lim_{\rho\to 0}\int_{C_\rho}\frac{e^{iz}}{z}dz=\pi i.$$
Therefore,
$$\int_0^\infty\frac{\sin x}{x}dx=\frac{\pi}{2}.$$