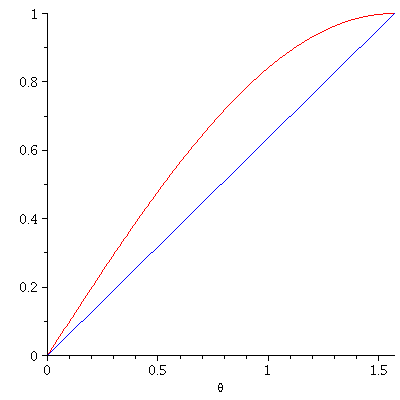
Suppose that

1. a function $f(z)$ is analytic at all points $z$ in the upper half plane $y\geq 0$ that are exterior to a circle $|z|=R_0$.
2. For any $z$ on $C_R: |z|=R>R_0$, there exists a positive real number $M_R>0$ such that $|f(z)|\leq M_R$ and $\lim_{R\to\infty}M_R=0$.

Then for any positive real number $a$,
$$\lim_{R\to\infty}\int_{C_R}f(z)e^{iaz}dz=0.$$

Proof. We first show Jordan’s Inequality
\begin{equation}\label{eq:jordan}\int_0^\pi e^{-R\sin\theta}d\theta<\frac{\pi}{R}\ (R>0).\end{equation}

The graphs of y=sin(theta) (in red) and y=(2/pi)theta (in blue)

As shown in the figure, $\frac{2}{\pi}\theta\leq\sin\theta$ for $0\leq\theta\leq\frac{\pi}{2}$. If $R>0$, then $$e^{-R\sin\theta}\leq e^{-2R\theta/\pi},\ 0\leq\theta\leq\frac{\pi}{2}.$$So, we have
\begin{align*}
\int_0^{\frac{\pi}{2}}e^{-R\sin\theta}d\theta&\leq\int_0^{\frac{\pi}{2}}e^{-2R\theta/\pi}d\theta\\
&=\frac{\pi}{2R}(1-e^{-R})\\
&<\frac{\pi}{2R}.
\end{align*}Since the graph of $y=\sin\theta$ is symmetric about $\theta=\frac{\pi}{2}$ on the interval $0\leq\theta\leq\pi$,
$$\int_0^\pi e^{-R\sin\theta}d\theta=2\int_0^{\frac{\pi}{2}}e^{-R\sin\theta}d\theta<\frac{\pi}{R}.$$

Let $C_R$ denote the positively oriented circle $z=Re^{i\theta}$ where $0\leq\theta\leq\pi$. Then
$$\int_{C_R}f(z)e^{iaz}dz=\int_0^\pi f(Re^{i\theta})\exp(iaRe^{i\theta})iRe^{i\theta}d\theta$$
and so
\begin{align*}
\left|\int_{C_R}f(z)e^{iaz}dz\right|&\leq M_RR\int_0^\pi e^{-aR\sin\theta}d\theta\\
&<\frac{M_R\pi}{a}\ (\mbox{by Jordan Inequality \eqref{eq:jordan}})\\
&\to 0
\end{align*}
as $R\to\infty$ since by assumption $\lim_{R\to\infty}M_R=0$.