In this lecture, we derive Fresnel integrals
$$\int_0^\infty\cos(x^2)dx=\int_0^\infty\sin(x^2)dx=\frac{1}{2}\sqrt{\frac{\pi}{2}},$$
which appear in optics and diffraction theory.

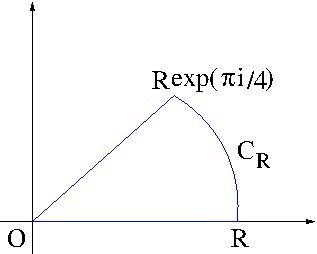
Let us consider a contour shown in the following figure.

As seen in the figure, $C_R$ is a part of the circle $z=Re^{i\theta}$, where $0\leq\theta\leq\frac{\pi}{4}$. Let $f(z)=e^{iz^2}$. Then $f(z)$ is analytic on and within the positively oriented simple closed contour $C$ shown in the figure. So, we have $\int_Cf(z)dz=0$ which amounts to the following expression:
$$\int_0^Re^{ix^2}dx+\int_{C_R}e^{iz^2}dz-\int_0^Re^{-r^2}\left(\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}\right)dr=0.$$
Separating this expression into the real and the imaginary parts, we obtain
\begin{align}
\label{eq:cos}
\int_0^R\cos(x^2)dx&=\frac{1}{\sqrt{2}}\int_0^Re^{-r^2}dr-\mathrm{Re}\int_{C_R}e^{iz^2}dz,\\
\label{eq:sin}
\int_0^R\sin(x^2)dx&=\frac{1}{\sqrt{2}}\int_0^Re^{-r^2}dr-\mathrm{Im}\int_{C_R}e^{iz^2}dz.
\end{align}
\begin{align*}
\left|\int_{C_R}e^{iz^2}dz\right|&=\left|\int_0^{\frac{\pi}{4}}e^{iR^2e^{2i\theta}}Rie^{i\theta}d\theta\right|\\
&\leq R\int_0^{\frac{\pi}{4}}|e^{iR^2e^{2i\theta}}|d\theta\\
&=R\int_0^{\frac{\pi}{4}}e^{-R^2\sin 2\theta}d\theta\\
&=\frac{R}{2}\int_0^{\frac{\pi}{2}}e^{-R^2\sin\phi}d\phi\ (\mbox{by subsitution}\ \phi=2\theta)\\
&=\frac{R}{4}\int_0^\pi e^{-R^2\sin\phi}d\phi\\
&<\frac{R}{4}\frac{\pi}{R^2}\\
&=\frac{\pi}{4R}\to 0
\end{align*}
as $R\to\infty$. The inequality in the second line to the last was obtained by Jordan’s Inequality. Hence, as $R\to\infty$ \eqref{eq:cos} and \eqref{eq:sin} become
\begin{align*}
\int_0^\infty\cos(x^2)dx&=\int_0^\infty\sin(x^2)dx\\
&=\frac{1}{\sqrt{2}}\int_0^\infty e^{-r^2}dr\\
&=\frac{1}{2}\sqrt{\frac{\pi}{2}}.
\end{align*}