Linear Approximation of $f(x)$ at $a$
As seen in differential calculus, when $x$ is near $a$ the function $f(x)$ can be approximated by the tangent line to $y=f(x)$ at $a$. (For details see here.) \begin{equation}\label{eq:linapprox}T_1(x)=f(a)+f'(a)(x-a)\end{equation} Note that $T_1(a)=f(a)$ and $T_1′(a)=f'(a)$.
Quadratic Approximation of $f(x)$ at $a$
If the graph of $y=f(x)$ is curved a lot near $a$, a polynomial of higher degree may be preferred for a better approximation, for instance a quadratic polynomial. Let us call such polynomial $T_2(x)$. We require that $T_2(x)$ satisfies $T_2(a)=f(a)$, $T_2′(a)=f'(a)$ and $T_2^{\prime\prime}(a)=f^{\prime\prime}(a)$. We can find $T_2(x)$ be setting $$T_2(x)=f(a)+f'(a)(x-a)+cf^{\prime\prime}(a)(x-a)^2$$ Then the condition $T_2^{\prime\prime}(a)=f^{\prime\prime}(a)$ implies that $c=\frac{1}{2}$. Hence \begin{equation}\label{eq:quadapprox}T_2(x)=f(a)+f'(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2\end{equation} There is a reason for the appearance of the factorial notation in the leading coefficient.
Example. Approximation for $\ln x$.
- Find the linear approximation to $f(x)=\ln x$ at $a=1$.
- Find the quadratic approximation to $f(x)=\ln x$ at $a=1$.
- Use these approximations to estimate the value of $\ln(1.05)$.
Solution. $f'(x)=\frac{1}{x}$ and $f^{\prime\prime}(x)=-\frac{1}{x^2}$. So
- $T_1(x)=x-1$ and
- $T_2(x)=(x-1)-\frac{1}{2}(x-1)^2$.
- $T_1(1.05)=0.05$ and $T_2(1.05)=0.04875$. For comparison, the actual value of $\ln(1.05)$ is $0.04879016417\cdots$.
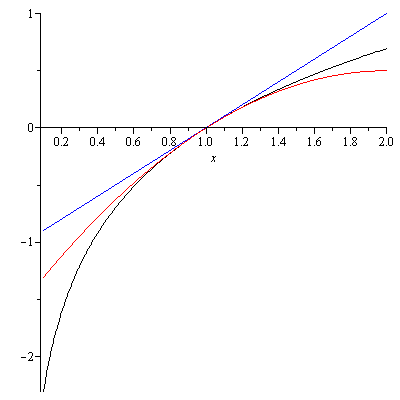
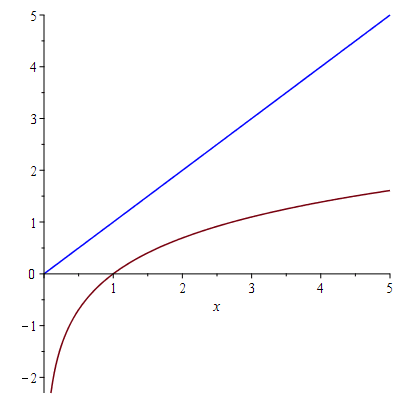
The graphs of y=ln(x) (in black), T_1(x)=x-1 (in blue) and T_2(x)=(x-1)-(x-2)^2/2 (in red)
The $n$-th Order Approximation of $f(x)$ at $a$
The $n$-th order approximation is given by the Taylor polynomial $T_n(x)$ centered at $a$ \begin{equation}\label{eq:taylorpolynomial}T_n(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n\end{equation}
Example. Find the Taylor polynomials $T_1,T_2,\cdots,T_7$ for $f(x)=\sin x$ at $a=0$.
Solution. $T_1(x)=T_2(x)=x$, $T_3(x)=T_4(x)=x-\frac{x^3}{3!}$, $T_5(x)=T_6(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}$, $T_7(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}$.
Example. Use Taylor polynomials of order $n=0,1,2,3$ to approximate $\sqrt{18}$.
Solution. There are two things we need to choose $f(x)$ and $a$. Obviously the function we need to use is $f(x)=\sqrt{x}$. How do we choose $a$ then? There are two things to consider for choosing a suitable $a$. One is $a$ has to be close to 18 and the other is $f(a)=\sqrt{a}$ is a number that can be calculated without a calculator. If we are allowed to use a calculator, the point of doing an approximation is moot. Besides, this is how people were able to calculate a number like $\sqrt{18}$ along time ago when calculators did not exist. In fact, calculators or computers cannot calculate the exact $\sqrt{18}$. What they can do is also approximations using the Taylor polynomials. With the two things in mind, the suitable choice for $a$ would be $a=16$. $f'(x)=\frac{1}{2\sqrt{x}}$, $f^{\prime\prime}(x)=-\frac{1}{4x\sqrt{x}}$, $f^{\prime\prime\prime}(x)=\frac{3}{8x^2\sqrt{x}}$. So, \begin{align*}T_0(x)&=\sqrt{16}=4\\T_1(x)&=4+\frac{1}{8}(x-16)\\T_2(x)&=4+\frac{1}{8}(x-16)-\frac{1}{512}(x-16)^2\\T_3(x)&=4+\frac{1}{8}(x-16)-\frac{1}{512}(x-16)^2+\frac{1}{16,384}(x-16)^3\end{align*} Hence, $T_0(18)=4$, $T_1(18)=4.25$, $T_2(18)=4.242188$, $T_3(18)=4.242676$. The actual value is $\sqrt{18}=4.242640686\cdots$.
When a function $f(x)$ is approximated by a Taylor polynomial $T_n(x)$, the error bound must also be taken into consideration because it can tell us about the accuracy of the approximation. The error is given by the remainder \begin{equation}\label{eq:remainder}R_n(x)=f(x)-T_n(x)\end{equation}
Theorem (Taylor’s Theorem). Let $f$ have continuous derivatives up to $f^{(n+1)}$ on an open interval $I$ containing $a$. Then for all $x$ in $I$, $$f(x)=T_n(x)+R_n(x),$$ where $T_n(x)$ is the $n$-th order Taylor polynomial for $f$ centered at $a$ and the remainder $R_n$ is \begin{equation}\label{eq:remainder2}R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1}\end{equation} for some $\xi$ between $x$ and $a$.
Remark. Recall the Mean Value Theorem: If $f(x)$ is continuous on $[a,x]$ and is differentiable on $(a,x)$, then there exists $a<\xi<x$ such that $$\frac{f(x)-f(a)}{x-a}=f'(\xi)$$ or $$f(x)=f(a)+f'(\xi)(x-a)$$ Hence we see that the Taylor’s theorem is a generalization of the Mean Value Theorem.
\eqref{eq:remainder2} can be used to obtain the maximum error bound \begin{equation}\label{eq:errorbd}|R_n(x)|=|f(x)-T_n(x)|\leq M\frac{|x-a|^{n+1}}{(n+1)!}\end{equation}where $|f^{(n+1)}(\xi)|\leq M$ for all $\xi$ between $a$ and $x$.
Example.
- What is the maximum error possible in using the approximation $$\sin x\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}$$ when $-0.3\leq x\leq 0.3$? Use this approximation to find $\sin 12^\circ$, correct to six decimal places.
- For what values of $x$ is this approximation accurate to within 0.00005?
Solution.
- Recall from the second example above $x-\frac{x^3}{3!}+\frac{x^5}{5!}=T_5(x)=T_6(x)$ but we regard it as $T_6(x)$. The reason is that the error $R_6$ is smaller than $R_5$. (This choice is also consistent with the alternating series estimate because $-\frac{x^7}{7!}$ comes after the term $\frac{x^5}{5!}$. See below.) Since $|f^{(7)}(\xi)|=|\cos(\xi)|\leq 1$ for all $\xi$ between 0 and $x$, from \eqref{eq:errorbd}, we have $|R_6(x)|\leq\frac{|x|^7}{7!}=\frac{|x|^7}{5040}$. Since $|x|\leq 0.3$, $|R_6|\leq\frac{(0.3)^7}{5040}\approx 4.3\times 10^{-8}$. Thus the maximum possible error is $4.3\times 10^{-8}$. Note that $T_6(x)$ is an alternating series, so it is actually easier to use the remainder estimate for alternating series $$|R_6|\leq a_7=\frac{|x|^7}{7!}=\frac{|x|^7}{5040}$$ \begin{align*}\sin 12^\circ&=\sin\left(\frac{12\pi}{180}\right)\\&=\sin\left(\frac{\pi}{15}\right)\\&\approx\frac{\pi}{15}-\frac{\left(\frac{\pi}{15}\right)^3}{3!}+\frac{\left(\frac{\pi}{15}\right)^5}{5!}\\&\approx 0.207911694\end{align*} Using the maximum possible error, $$\sin 12^\circ=T_6\left(\frac{\pi}{15}\right)+R_6=0.207911694+0.0000000043=0.207911737$$ So $\sin 12^\circ$ correct to six decimal places is 0.207911.
- $\frac{|x|^7}{5040}<0.00005$ so $|x|^7<0.00005\times 5045=0.252$. Hence, $|x|<(0.252)^{\frac{1}{7}}\approx 0.821$.
Example.
- Approximate $f(x)=\root 3\of{x}$ by a Taylor polynomial of order (degree) 2 at $a=8$.
- How accurate is this approximation when $7\leq x\leq 9$?
Solution.
- First we find the following derivatives. \begin{align*}f'(x)&=\frac{1}{3}x^{-\frac{2}{3}}\\f^{\prime\prime}(x)&=-\frac{2}{9}x^{-\frac{5}{3}}\\f^{\prime\prime\prime}(x)&=\frac{10}{27}x^{-\frac{8}{3}}\end{align*} Now $$\root 3\of{x}\approx T_2(x)=2+\frac{1}{12}(x-8)-\frac{1}{288}(x-8)^2$$
- Note that the Taylor polynomial is not alternating when $x<8$. So we use \eqref{eq:remainder2} instead for the remainder estimation.\begin{align*}R_2(x)&=\frac{f^{\prime\prime\prime}(\xi)}{3!}(x-8)^3\\&=\frac{10}{27}\xi^{-\frac{8}{3}}\frac{(x-8)^3}{3!}\\&=\frac{5}{81}\frac{(x-8)^3}{\xi^{\frac{8}{3}}}\end{align*} If $7\leq x\leq 9$, $-1\leq x-8\leq 1$. Since $\xi>7$, $\xi^{\frac{8}{3}}>7^{\frac{8}{3}}>179$. Hence, $$|R_2(x)|\leq\frac{5}{81}\frac{|x-8|^3}{\xi^{\frac{8}{3}}}<\frac{5}{81}\cdot\frac{1}{179}\approx 0.00034485<0.0004$$
A Physical Application
In Einstein’s theory of special relativity, the mass of an object moving with velocity $v$ is \begin{equation}\label{eq:relmass}m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\end{equation} where $m_0$ is the mass of the object at rest and $c$ is the speed of light in vacuum spacetime. $m$ in \eqref{eq:relmass} is called the relativistic mass. The kinetic energy is the difference between its total energy and its energy at rest \begin{equation}\label{eq:kenergy}K=mc^2-m_0c^2\end{equation}
- Show that when $v\ll c$ (this means $v$ is very small compared with $c$), $K=\frac{1}{2}m_0v^2$.
- Use Taylor’s formula to estimate the difference in these expressions for $K$ when $|v|\leq 100$ m/s.
Solution.
- First note that \begin{align*}(1+x)^{-\frac{1}{2}}&=1-\frac{1}{2}x+\frac{\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)}{2!}x^2+\frac{\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\left(-\frac{5}{2}\right)}{3!}x^3+\cdots\\&=1-\frac{1}{2}x+\frac{3}{8}x^2-\frac{5}{16}x^3+\cdots\end{align*} (For details on how to obtain this read my note on Taylor series here, especially under The Binomial Series.) Thus, \begin{align*}K&=\frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}-m_0c^2\\&=m_0c^2\left[\left(1-\frac{v^2}{c^2}\right)^{-\frac{1}{2}}-1\right]\\&=m_0c^2\left[\left(1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{5}{16}\frac{v^6}{c^6}+\cdots\right)-1\right]\\&=m_0c^2\left(\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{5}{16}\frac{v^6}{c^6}+\cdots\right)\end{align*} Hence, if $v\ll c$ then $K\approx\frac{1}{2}m_0v^2$.
- $R_1(x)=\frac{f^{\prime\prime}(\xi)}{2!}x^2$ where $f(x)=m_0c^2[(1+x)^{-\frac{1}{2}}-1]$ with $x=-\frac{v^2}{c^2}$. $f^{\prime\prime}(x)=\frac{3}{4}m_0c^2(1+x)^{-\frac{5}{2}}$ so $R_1(x)=\frac{3m_0c^2}{8(1+\xi)^{\frac{5}{2}}}\cdot\frac{v^4}{c^4}$ where $-\frac{v^2}{c^2}<\xi<0$. With $c=3\times 10^8$ m/s and $|v|\leq 100$ m/s. we obtain \begin{align*}R_1(x)&\leq\frac{3m_0(9\times 10^{16})}{8\left(1-\frac{100^2}{c^2}\right)^{\frac{5}{2}}}\left(\frac{100}{c}\right)^4\\&<(4.17\times 10^{-10})m_0\end{align*}