The Alternating Series Test

The alternating series $\sum_{k=1}^\infty (-1)^{k+1}a_k$ converges provided:

1. $0<a_{k+1}\leq a_k$ for all $k=1,2,3,\cdots$ i.e. $\{a_k\}$ is a decreasing sequence.
2. $\lim_{k\to\infty}a_k=0$.

Example. The alternating harmonic series $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k}$ converges.

Example. The alternating series $\sum_{k=1}^\infty(-1)^{k+1}\frac{k+1}{k}$ diverges because $\lim_{k\to\infty}\frac{k+1}{k}=1\ne 0$.

Example. The alternating series $\sum_{k=2}^\infty(-1)^k\frac{\ln k}{k}$ converges because

1. $\left\{\frac{\ln k}{k}\right\}$ is decreasing for all $n\geq 3$. (Let $f(x)=\frac{\ln x}{x}$. Then $f'(x)=\frac{1-\ln x}{x^2}<0$ for all $x>e=2.7182818284590\cdots$.)
2. $\lim_{k\to\infty}\frac{\ln k}{k}=0$.

Remainder in Alternating Series

Let $S=\sum_{k=1}^\infty(-1)^{k+1}a_k=a_1-a_2+a_3-a_4+\cdots$. Then we see that the distribution of its partial sums would be like the following figure.

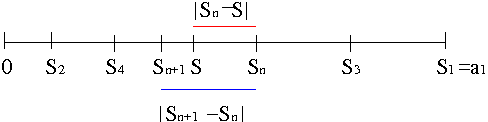
From the figure, we obtain the inequality \begin{equation}\label{eq:altser}|R_n|=|S-S_n|\leq|S_{n+1}-S_n|=a_{n+1}\end{equation} The inequality \eqref{eq:altser} can serve as an estimate for the error (remainder) $|R_n|$ whose error bound is given by $a_{n+1}$.

Example.

1. How many terms of the series $$\ln 2=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k}$$ are required to approximate the value of the series with a remainder less than $10^{-6}$?
2. If $n=9$ terms of the series $\sum_{k=1}^\infty\frac{(-1)^k}{k!}=e^{-1}-1$ are summed, what is the maximum error committed in approximating the value of the series?

Solution.

1. $|R_n|\leq a_{n+1}=\frac{1}{n+1}<10^{-6}$ so $n+1>1000000$ i.e. $n\geq 1000000$.
2. $|R_9|\leq\frac{1}{10!}\approx 2.8\times 10^{-7}$.

Absolute and Conditional Convergence

Assume that $\sum_{k=1}^\infty a_k$ converges. $\sum_{k=1}^\infty a_k$ is said to converge absolutely if $\sum_{k=1}^\infty |a_k|$ converges. Otherwise, $\sum_{k=1}^\infty a_k$ converges conditionally.

Example. The alternating harmonic series $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{k}$ converges conditionally.

Theorem. If $\sum_{k=1}^\infty |a_k|$ converges, then so does $\sum_{k=1}^\infty a_k$. That is, absolute convergence implies convergence. However, the converse need not be true as seen in the example above.

Proof. \begin{align*}\sum_{k=1}^\infty a_k&=\sum_{k=1}^\infty(a_k+|a_k|-|a_k|)\\&=\sum_{k=1}^\infty(a_k+|a_k|)-\sum_{k=1}^\infty|a_k|\end{align*} Since $0\leq a_k+|a_k|\leq 2|a_k|$, $\sum_{k=1}^\infty(a_k+|a_k|)$ converges. Therefore, $\sum_{k=1}^\infty a_k$ converges.

Example. Determine whether each of the following series diverges, converge absolutely, or converge conditionally.

1. $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{\sqrt{k}}$
2. $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{\sqrt{k^3}}$
3. $\sum_{k=1}^\infty\frac{\sin k}{k^2}$
4. $\sum_{k=1}^\infty\frac{(-1)^kk}{k+1}$

Solution.

1. By the alternating series test, the series converges. However, $\sum_{k=1}^\infty\frac{1}{\sqrt{k}}$ is a $p$-series with $p=\frac{1}{2}<1$, so it diverges. Hence, $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{\sqrt{k}}$ converges conditionally.
2. $\sum_{k=1}^\infty\frac{1}{\sqrt{k^3}}$ is a $p$-series with $p=\frac{3}{2}>1$, so it converges. Therefore, $\sum_{k=1}^\infty\frac{(-1)^{k+1}}{\sqrt{k^3}}$ converges absolutely.
3. $|\sin k|\leq 1$, so $\frac{|\sin k|}{k^2}\leq\frac{1}{k^2}$. Since $\sum_{k=1}^\infty\frac{1}{K^2}$ converges, so does $\sum_{k=1}^\infty\frac{|\sin k|}{k^2}$ by the comparison test. Therefore, $\sum_{k=1}^\infty\frac{\sin k}{k^2}$ converges absolutely.
4. $\lim_{k\to\infty}\frac{k}{k+1}=1\ne 0$ so the alternating series diverges.