d’Alembert-Cauchy Ratio Test
The following d’Alembert-Cauchy ratio test is one of the easiest to apply and is widely used.
Theorem (d’Alembert-Cauchy Ratio Test). Suppose that $\sum_{n=1}^\infty a_n$ is a series with positive terms.
- If $\lim_{n\to\infty}\frac{a_{n+1}}{a_n}<1$ then $\sum_{n=1}^\infty a_n$ converges.
- If $\lim_{n\to\infty}\frac{a_{n+1}}{a_n}>1$ then $\sum_{n=1}^\infty a_n$ diverges.
- If $\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=1$ then $\sum_{n=1}^\infty a_n$ then the convergence is indeterminant, i.e., the ratio test provides no information regarding the convergence of the series $\sum_{n=1}^\infty a_n$.
Example. Test $\sum_{n=1}^\infty\frac{n}{2^n}$ for convergence.
Solution. \begin{align*}\lim_{n\to\infty}\frac{a_{n+1}}{a_n}&=\lim_{n\to\infty}\frac{\frac{n+1}{2^{n+1}}}{\frac{n}{2^n}}\\&=\lim_{n\to\infty}\frac{n+1}{2n}\\&=\frac{1}{2}<1\end{align*} Hence by the ratio test the series converges.
Example. Test the convergence of the series $\sum_{n=1}^\infty\frac{n^n}{n!}$.
Solution.
\begin{align*}
\lim_{n\to\infty}\frac{a_{n+1}}{a_n}&=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n\\
&=e>1.
\end{align*}
Hence, the series diverges.
Remark. There is an easier way to show the divergence of the series $\sum_{n=1}^\infty\frac{n^n}{n!}$.
Note that
$$a_n=\frac{n^n}{n!}=\frac{n\cdot n\cdot n\cdots n}{1\cdot 2\cdot 3\cdots n}\geq n.$$
This implies that $\lim_{n\to\infty}a_n=\infty$. Hence by the divergence test the series diverges.
Cauchy Root Test
Theorem (Cauchy Root Test). Suppose that $\sum_{n=1}^\infty a_n$ be a series with positive terms.
- If $\lim_{n\to\infty}\root n\of{a_n}=r<1$ then $\sum_{n=1}^\infty a_n$ converges.
- If $\lim_{n\to\infty}\root n\of{a_n}=r> 1$ then $\sum_{n=1}^\infty a_n$ diverges.
- If $\lim_{n\to\infty}\root n\of{a_n}=r=1$ then the test fails, i.e., the root test is inclusive.
Example. Test the convergence of the series $\sum_{n=1}^\infty\left(\frac{2n+3}{3n+2}\right)^n$.
Solution. \begin{align*}\lim_{n\to\infty}\root n\of{a_n}&=\lim_{n\to\infty}\root n\of{\left(\frac{2n+3}{3n+2}\right)^n}\\&=\lim_{n\to\infty}\frac{2n+3}{3n+2}\\&=\frac{2}{3}<1\end{align*}Hence by the root test the series converges.
Comparison Test
Theorem (Comparison Test). Suppose that $\sum_{n=1}^\infty a_n$ and $\sum_{n=1}^\infty b_n$ be series with positive terms.
- If $\sum_{n=1}^\infty b_n$ converges and $a_n\leq b_n$ for all $n$, then $\sum_{n=1}^\infty a_n$ also converges.
- If $\sum_{n=1}^\infty b_n$ diverges and $b_n\leq a_n$ for all $n$, then $\sum_{n=1}^\infty a_n$ also diverges.
Remark. For a convergent series we have the geometric series, whereas the harmonic series will serve as a divergent series. As other series are identified as either convergent or divergent, they may be used for the known series in this comparison test.
Example. Determine whether the series $\sum_{n=1}^\infty\frac{5}{2n^2+4n+3}$ converges.
Solution. Notice that $\frac{5}{2n^2+4n+3}<\frac{5}{n^2}$ for all $n$. Since $\sum_{n=1}\frac{1}{n^2}$ converges (it is a $p$-series with $p=2$), by the comparison test the series converges.
Example. Test the series $\sum_{n=1}^\infty\frac{n^3}{2n^4-1}$ for convergence or divergence.
Solution. $2n^4-1<2n^4$ so $\frac{n^3}{2n^4-1}>\frac{n^3}{2n^4}=\frac{1}{2n}$. Since the harmonic series $\sum_{n=1}^\infty\frac{1}{n}$ diverges, the series diverges.
Example. Test the series $\sum_{n=2}^\infty\frac{\ln n}{n}$ for convergence or divergence.
Solution. $\left(\frac{\ln x}{x}\right)’=\frac{1-\ln x}{x^2}<0$ on $(e,\infty)$ i.e. $\frac{\ln n}{n}>\frac{1}{n}$ for all $n\geq 3$. Since $\sum_{n=1}^\infty\frac{1}{n}$ diverges (the harmonic series, also $p$-series with $p=1$), by the comparison test, the series diverges.
Example. Test the series $\sum_{n=2}^\infty\frac{\ln n}{n^3}$ for convergence or divergence.
Solution. As seen in the following figure, $\ln n<n$ for all $n\geq 2$.
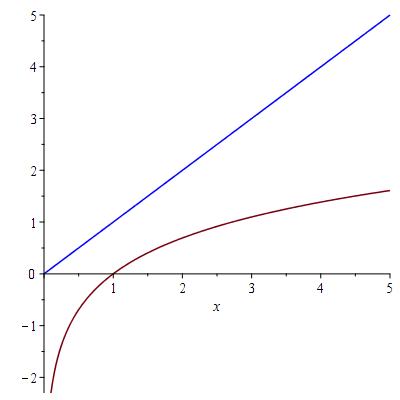
The graphs of y=ln(x) (in red) and y=x (in blue).
So $\frac{\ln n}{n^3}<\frac{n}{n^3}=\frac{1}{n^2}$. Since $\sum_{n=1}^\infty\frac{1}{n^2}$ converges ($p$-series with $p=2>1$), $\sum_{n=2}^\infty\frac{\ln n}{n^3}$ also converges.
Example (The $p$ series). Let $p\leq 1$ Then
$\frac{1}{n}<\frac{1}{n^p}$ for all $n$, so by the Comparison Test
$\sum_{n=1}^\infty\frac{1}{n^p}$ is divergent for all $p\leq 1$.
The Limit Comparison Test
The limit comparison Test is a variation of the comparison test.
Theorem (The Limit Comparison Test). Suppose that $\sum_{n=1}^\infty a_n$ (this is the test subject) and $\sum_{n=1}^\infty b_n$ (this is the series you know its convergence or divergence) are series with positive terms. Let $L=\lim_{n\to\infty}\frac{a_n}{b_n}$. Then the following holds.
- If $0<L<\infty$, then either both series converge or both diverge.
- If $L=0$ and $\sum_{n=1}^\infty b_n$ converges, then $\sum_{n=1}^\infty a_n$ converges.
- If $L=\infty$ and $\sum_{n=1}^\infty b_n$ diverges, then $\sum_{n=1}^\infty a_n$.
The limit comparison test is inconclusive otherwise.
Remark. Just like the comparison test the hardest part of using the limit comparison test is choosing a right series for $\sum_{n=1}^\infty b_n$ and unfortunately there is no systematic way of choosing a right one. It just depends on the given series. It could be a geometric series as you will see in an example below. For certain types of series, a good candidate for $b_n$ is $\frac{1}{n^p}$ from the $p$-series with an appropriate $p$-value.
Example. Test the series $\sum_{n=1}^\infty\frac{1}{2^n-1}$ for convergence or divergence.
Solution. Considering that $a_n=\frac{1}{2^n-1}$ and the geometric series $\sum_{n=1}^\infty\frac{1}{2^n}$ converges, it would be reasonable to try $b_n=\frac{1}{2^n}$. \begin{align*}\lim_{n\to\infty}\frac{a_n}{b_n}&=\lim_{n\to\infty}\frac{2^n}{2^n-1}\\&=\lim_{n\to\infty}\frac{1}{1-\frac{1}{2^n}}\\&=1\end{align*} Since $\sum_{n=1}^\infty\frac{1}{2^n}$ converges, so should $\sum_{n=1}^\infty\frac{1}{2^n-1}$ by the limit comparison test.
Example. Test the series $\sum_{n=1}^\infty\frac{1}{\sqrt{n^2+1}}$ for convergence or divergence.
Solution. The dominant part of $a_n=\frac{1}{\sqrt{n^2+1}}$ is $\frac{1}{\sqrt{n^2}}=\frac{1}{n}$ so we choose $b_n=\frac{1}{n}$. Then \begin{align*}\lim_{n\to\infty}\frac{a_n}{b_n}&=\lim_{n\to\infty}\frac{n}{\sqrt{n^2+1}}\\&=\lim_{n\to\infty}\frac{1}{\sqrt{1+\frac{1}{n^2}}}\\&=1\end{align*} Since $\sum_{n=1}^\infty\frac{1}{n}$ diverges, so should $\sum_{n=1}^\infty\frac{1}{\sqrt{n^2+1}}$ by the limit comparison test.
Example. Test the series $\sum_{n=1}^\infty\frac{n^4-2n^2+3}{2n^6-n+5}$ for convergence or divergence.
Solution. The dominant part of $a_n$ is $\frac{n^4}{n^6}=\frac{1}{n^2}$ so we choose $b_n=\frac{1}{n^2}$. Then $$\frac{\frac{n^4-2n^2+3}{2n^6-n+5}}{\frac{1}{n^2}}=\frac{n^6-2n^4+3n^2}{2n^6-n+5}\to\frac{1}{2}$$ as $n\to\infty$. Since $\sum_{n=1}^\infty\frac{1}{n^2}$ converges, so does the given series by the limit comparison test.
Example. Test the series $\sum_{n=1}^\infty\frac{\ln n}{n^2}$ for convergence or divergence.
Solution. In this case, we try the $p$-series but we don’t know what $p$-value may work. To figure it out, let $b_n=\frac{1}{n^p}$. Then $\frac{a_n}{b_n}=\frac{\frac{\ln n}{n}}{\frac{1}{n^p}}=\frac{\ln n}{n^{2-p}}$. If $p\geq 2$ then $\lim_{n\to\infty}\frac{a_n}{b_n}=\infty$ but $\sum_{n=1}^\infty b_n$ converges so the test is inconclusive. This means that $p<2$. Now, using the L’Hôpital’s rule we get $$\lim_{n\to\infty}\frac{a_n}{b_n}=\lim_{n\to\infty}\frac{1}{(2-p)n^{2-p}}=0$$ If $p\leq 1$ then $\sum_{n=1}^\infty b_n$ diverges so the test would be inconclusive. This would leave us the condition $1<p<2$ for the limit comparison test to work. This means that for any value of $1<p<2$ the limit comparison test will tell us that the series $\sum_{n=1}^\infty\frac{\ln n}{n^2}$ converges. For instance, let us choose $p=\frac{3}{2}$. Then $$\frac{a_n}{b_n}=\frac{\ln n}{\sqrt{n}}\to 0$$ as $n\to\infty$. Since $\sum_{n=1}^\infty\frac{1}{n^{\frac{3}{2}}}$ converges, the series converges.
Remark. Doing the same analysis we did in the example above, we can also see why using the dominant part of $a_n$ worked out in some earlier examples. For instance, consider the series $\sum_{n=1}^\infty\frac{n^4-2n^2+3}{2n^6-n+5}$ that we discussed earlier. Again $a_n=\frac{n^4-2n^2+3}{2n^6-n+5}$ and let $b_n=\frac{1}{n^p}$. An appropriate $p$-value is yet to be determined. Now $\frac{a_n}{b_n}=\frac{n^{p-2}-2n^{p-4}+3n^{p-6}}{2-\frac{1}{n^5}+\frac{5}{n^6}}$. First, if $p\leq 1$, the $p$-series $\sum_{n=1}^\infty\frac{1}{n^p}$ diverges but $\lim_{n\to\infty}\frac{a_n}{b_n}=0$ so the test is inconclusive and hence $p>1$ in which case the $p$-series converges. If $p>2$ then $\lim_{n\to\infty}\frac{a_n}{b_n}=\infty$ which makes the test inconclusive. Therefore we see that $1<p\leq 2$. $p=2$ is what we get from the dominant part $\frac{n^4}{n^6}$ of $a_n$. But that is not the only choice. You can choose any $1<p\leq 2$ in order for the test to work, for example your could’ve chosen $p=\frac{3}{2}$ in which case $\lim_{n\to\infty}\frac{a_n}{b_n}=0$. The limit comparison test says then the series converges.
