In this posting, we discuss limits of trigonometric functions. The most basic trigonometric functions are of course \(y=\sin x\) and \(y=\cos x\). They have the following limit properties.
Theorem 5. For any \(a\in\mathbb R\), \[\lim_{x\to a}\sin x=\sin a,\ \lim_{x\to a}\cos x=\cos a.\]
You notice that both \(y=\sin x\) and \(y=\cos x\) satisfy the same limit property as polynomial functions (Theorem 2 in Lecture 4). This is not a coincidence and the reason behind this is that polynomial functions, \(y=\sin x\) and \(y=\cos x\) are continuous functions. This will become clear when we discuss the continuity of a function later. Limit properties of other trigonometric function will stem out automatically from the above Theorem 5 and Theorem 1 in Lecture 4. For example, the limit property of \(y=\tan x\) is given by \[\lim_{x\to a}\tan x=\lim_{x\to a}\frac{\sin x}{\cos x}=\frac{\sin a}{\cos a}=\tan a,\] where \(\tan a\) is defined or equivalently \(\cos a\ne 0\).
Theorem 6. Suppose that \(f(x)\leq g(x)\) near \(x=a\) and both \(\displaystyle\lim_{x\to a}f(x)\), \(\displaystyle\lim_{x\to a}g(x)\) exist. Then \[\lim_{x\to a}f(x)\leq \lim_{x\to a}g(x).\]
Corollary 7. [Squeeze Theorem, Sandwich Theorem] Suppose that \(f(x)\leq g(x)\leq h(x)\) near \(x=a\). If \(\displaystyle\lim_{x\to a}f(x)=\lim_{x\to a}h(x)=L\) then \[\lim_{x\to a}g(x)=L.\]
Squeeze Theorem is useful to calculate certain type of limits such as the following example.
Example. Find the limit \(\displaystyle\lim_{x\to 0}x^2\sin\frac{1}{x}\).
Solution. Since \(-1\leq\sin\frac{1}{x}\leq 1\), \[-x^2\leq x^2\sin\frac{1}{x}\leq x^2\] for all \(x\ne 0\). Since \(\displaystyle\lim_{x\to 0}(-x^2)=\lim_{x\to 0}x^2=0\), by Squeeze Theorem \[\lim_{x\to 0}x^2\sin\frac{1}{x}=0.\] The following picture also confirms our result.
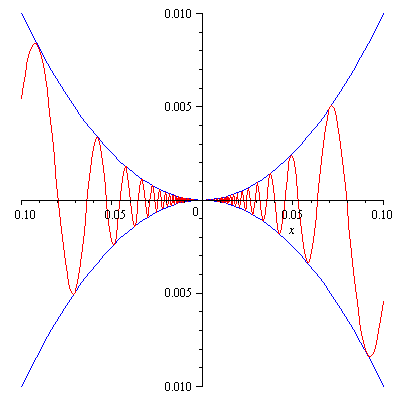
There is another important limit that involves a trigonometric function. It is
Theorem 8. \(\displaystyle\lim_{x\to 0}\frac{\sin x}{x}=1\).
This is an important formula. You will readily see that this limit is \(\frac{0}{0}\) type indeterminate form. So this means that \(\sin x\) must have a factor \(x\) in it. But how do we factor \(\sin x\)? It is not a polynimial! In fact. it is (sort of). This is something you are going to learn in Calculus 3 (MAT 169) but I want you to taste it. The function \(\sin x\) is can be written as a never-ending polynomial (such a polynomial is called a power series in mathematics) \[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots,\]where \(n!\) denotes the \(n\) factorial\[n!=n(n-1)(n-2)(n-3)\cdots3\cdot 2\cdot 1.\] So \begin{eqnarray*}\lim_{x\to 0}\frac{\sin x}{x}&=&\lim_{x\to 0}\frac{x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots}{x}\\&=&\lim_{x\to 0}\left(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots\right)\\&=&1.\end{eqnarray*}
We have now confirmed that the formula is indeed correct, but is there a more fundamental proof without using power series? Yes, there is. In fact it can be proved using trigonometry. First consider the case when \(x\to 0+\). In this case, without loss of generality we may assume that \(x\) is an acute angle so we have the following picture.
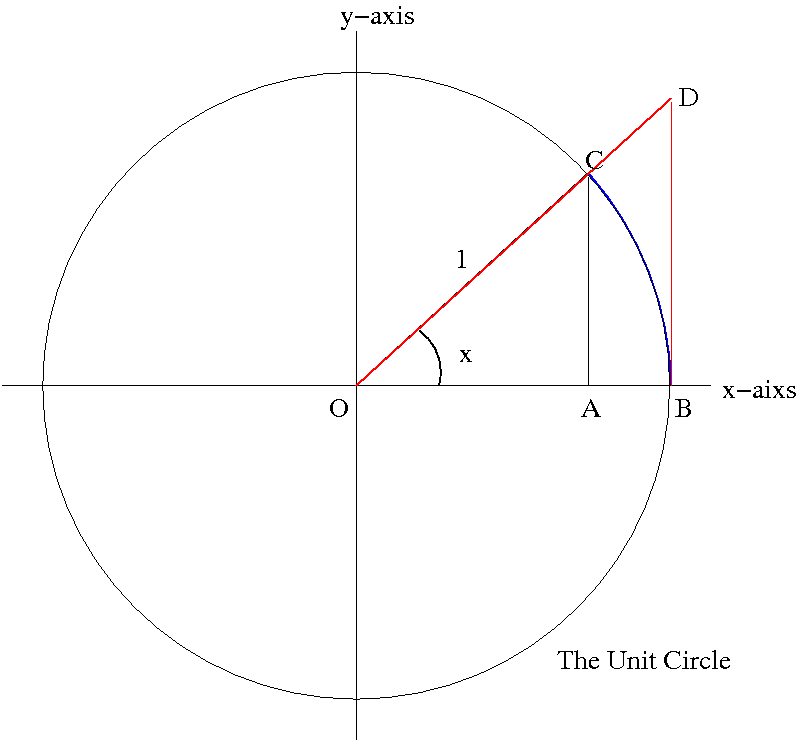
The areas of \(\triangle OAC\), \(\sphericalangle OBC\) and \(\triangle OBD\) are, respectively, given by \(\frac{1}{2}\cos x\sin x\), \(\frac{1}{2}x\) and \(\frac{1}{2}\tan x\). Clearly from the picture they satisfy the inequality \[\frac{1}{2}\cos x\sin x<\frac{1}{2}x<\frac{1}{2}\tan x.\] Dividing this inequality by \(\frac{1}{2}\sin x\) (note that \(\sin x>0\) since \(x\) is an acute angle) we obtain\[\cos x<\frac{x}{\sin x}<\frac{1}{\cos x}\] or equivalently,\[\frac{1}{\cos x}<\frac{\sin x}{x}<\cos x.\] Now \(\displaystyle\lim_{x\to 0+}\cos x=\lim_{x\to 0+}\frac{1}{\cos x}=1\), so by Squeeze Theorem,\[\lim_{x\to 0+}\frac{\sin x}{x}=1.\] Similarly, we can also show that\[\lim_{x\to 0-}\frac{\sin x}{x}=1.\] Hence completes the proof.
Example. Find $\displaystyle\lim_{x\to 0}\frac{\sin 7x}{4x}$.
Solution. \begin{eqnarray*}\lim_{x\to 0}\frac{\sin 7x}{4x}&=&\lim_{x\to 0}\frac{7}{4}\frac{\sin 7x}{7x}\\&=&\frac{7}{4}\lim_{x\to 0}\frac{\sin 7x}{7x}\\&=&\frac{7}{4}\ \left(\lim_{x\to 0}\frac{\sin 7x}{7x}=1\right).\end{eqnarray*}
Example. Find $\displaystyle\lim_{\theta\to 0}\frac{\cos\theta-1}{\theta}$.
Solution. \begin{eqnarray*}\lim_{\theta\to 0}\frac{\cos\theta-1}{\theta}&=&\lim_{\theta\to 0}\frac{\cos\theta-1}{\theta}\frac{\cos\theta+1}{\cos\theta+1}\\&=&\lim_{\theta\to 0}\frac{\cos^2\theta-1}{\theta(\cos\theta+1)}\\&=&\lim_{\theta\to 0}\frac{\cos^2\theta-1}{\theta(\cos\theta+1)}\\&=&\lim_{\theta\to 0}\frac{-\sin^2\theta}{\theta(\cos\theta+1)}\\&=&-\lim_{\theta\to 0}\frac{\sin\theta}{\theta}\frac{\sin\theta}{\cos\theta+1}\\&=&-\lim_{\theta\to 0}\frac{\sin\theta}{\theta}\cdot\lim_{\theta\to 0}\frac{\sin\theta}{\cos\theta+1}\\&=&-1\cdot 0=0.\end{eqnarray*}

Pingback: Derivatives of Trigonometric Functions | MathPhys Archive
Pingback: Polynomial theorem | Lesservicesnrj
Pingback: Cos Tan 1 | More More Pics