Often you hear that Einstein’s relativity prevents FTL (Faster-Than-Light). Is that true? The answer is yes and no. It is not possible for a spaceship to travel faster than the speed of light. But there may be a particle that travels FTL and the existence of such a particle would not violate the principles of relativity if its speed already exceeds the speed of light when it is created. The hypothetical particle that travels FTL is called a tachyon. (tachys means fast in Greek) The name was coined by a Columbia University physicist Gerald Feinberg in 1967. When he was asked why he thought about such a particle Feinberg reportedly quoted a Jewish proverb “Everything which is not forbidden is allowed.” (Author’s note: This is from something I read more than 3 decades ago when I was a high school student so I cannot cite its source. Also I could not find any such Jewish proverb either. It is however a constitutional principle of English law.)

For a Tachyon, the Lorentz transformation is given by the complex coordinates \begin{align*}t’&=-i\frac{t-\frac{v}{c^2}x}{\sqrt{\frac{v^2}{c^2}-1}}\\x’&=-i\frac{x-vt}{\sqrt{\frac{v^2}{c^2}-1}}\end{align*} where $i=\sqrt{-1}$. Although this is a complex transformation, it is still an isometry i.e. it preserves the Minkowski metric. In order for its energy $E$ to be real one has to assume that its rest mass is purely imaginary $im_0$ where $m_0>0$ is real and hence from the relativistic energy $$E=\frac{im_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{im_0c^2}{i\sqrt{\frac{v^2}{c^2}-1}}=\frac{m_0c^2}{\sqrt{\frac{v^2}{c^2}-1}}$$ Imaginary rest mass may sound weird but rest mass is not an observable because a particle is never at rest. What’s important is energy being real as it is an observable. The following figure shows energies of a subluminal particle (in red) and a superluminal particle (in blue) with $m_0=c=1$).

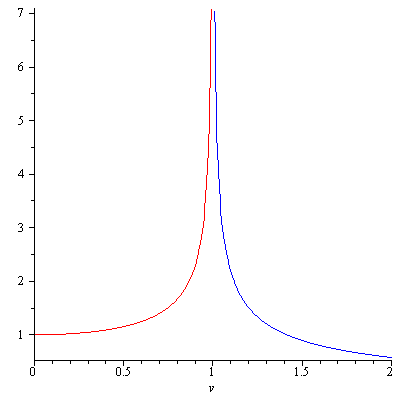
Properties of Tachyons:

1. The speed of light $c$ is the greatest lower bound of Tachyon’s speed. There is no upper limit of Tachyon’s speed.
2. Tachyons have imaginary rest mass (as we discussed above).
3. In order for a tachyon to slow down to the speed of light, it requires infinite amount of energy and momentum.
4. Another peculiar nature of tachyons. If a tachyon looses energy, its speed increases. At $E=0$, $v=\infty$.

How do we detect tachyons if they exist? Since tachyons travel FTL, we can’t see them coming. However if they are charged particles, they will emit electromagnetic Mach shock waves called Tscherenkov (also spelled Cherenkov) radiations. This always happens when charged particles are passing through a medium with a higher speed than the phase speed of light in the medium. By detecting such Tscherenkov radiations we may be able to confirm the existence of tachyons.

An interesting question is “can we use tachyons for FTL communications? ” It was answered by Richard C. Tolman as negative in his book [2] (pp 54-55). In [2]. Tolman considered the following thought experiment. Suppose a signal is being sent from a point $A$ (cause) to another point $B$ (effect) with speed $u$. In an inertial frame $S$ where $A$ and $B$ are at rest, the time of arrival at $B$ is given by $$\Delta t=t_B-t_A=\frac{B-A}{u}$$ In another inertial frame $S’$ moving with speed $v$ relative to $S$ the time of arrival at $B$ is given, according to the Lorentz transformation, by \begin{align*}\Delta t’&=t’_{B}-t’_{A}\\&=\frac{t_B-\frac{v}{c^2}x_B}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{t_A-\frac{v}{c^2}x_A}{\sqrt{1-\frac{v^2}{c^2}}}\\&=\frac{1-u\frac{v}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}\Delta t\end{align*} If $u>c$ then certain values of $v$ can make $\Delta t’$ negative. In other words, the effect occurs before the cause in this frame, the violation of causality!

Food for Thought: Can one possibly use tachyons to send a message (signal) to the past?

References:

1. Walter Greiner, Classical Mechanics, Point Particles and Relativity, Springer, 2004
2. Richard C. Tolman, The Theory of the Relativity of Motion, University of California Press, 1917. A scanned copy is available for viewing online here.