Let $\begin{pmatrix}
t\\
x
\end{pmatrix}$ be a vector in $tx$-plane and $\begin{pmatrix}
t’\\
x’
\end{pmatrix}$ denote its rotation by a hyperbolic angle $\phi$. Then as we have seen here we have:
\begin{equation}
\begin{aligned}
t’&=t\cosh\phi-x\sinh\phi\\
x’&=-t\sinh\phi+x\cosh\phi
\end{aligned}\label{eq:boost1}
\end{equation}
$t’$-axis ($x’=0$) is moving at a constant speed
\begin{equation}
\label{eq:velocity1}
v=\frac{x}{t}=\frac{\sinh\phi}{\cosh\phi}=\tanh\phi\end{equation}
while $x’$-axis ($t’=0$) is moving at a constant speed
\begin{equation}
\label{eq:velocity2}
v=\frac{x}{t}=\frac{\cosh\phi}{\sinh\phi}=\coth\phi
\end{equation}
This means that the time and spacial axes scissor together and hence the speed of light remains the same regardless of the coordinate transformation as illustrated in Figure 1. The picture in Figure 1 is called the spacetime diagram.

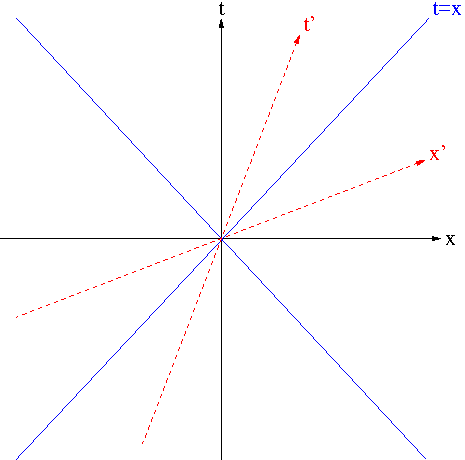
Figure 1. Spacetime Diagram

From Euclidean perspective, $t’$ and $x’$ do not appear to be orthogonal. However, from Lorentzian perspective they are orthogonal. To see that let $e_0=\begin{pmatrix}
1\\
0 \end{pmatrix}$ and $e_1=\begin{pmatrix}
0\\
1
\end{pmatrix}$. Also let $e_0’$ and $e_1’$ be the rotations of $e_0$ and $e_1$ by the hyperbolic angle $\phi$, respectively. Then by \eqref{eq:boost1} we have
$$e_0’=\begin{pmatrix}
\cosh\phi\\
-\sinh\phi
\end{pmatrix},\ e_1’=\begin{pmatrix}
-\sinh\phi\\
\cosh\phi
\end{pmatrix}$$
Now \begin{align*}\langle {e_0}’,e_1’\rangle&=(\cosh\phi\ -\sinh\phi)\begin{pmatrix}
-1 & 0\\
0 & 1
\end{pmatrix}\begin{pmatrix}
-\sinh\phi\\
\cosh\phi
\end{pmatrix}\\&=\cosh\phi\sinh\phi-\sinh\phi\cosh\phi=0\end{align*} So $e_0’$ and $e_1’$ are orthogonal.

\eqref{eq:boost1} with \eqref{eq:velocity1} can be written as
\begin{align*}
t’&=\cosh\phi(t-vx)\\
x’&=\cosh\phi(x-vt)
\end{align*}
Using the well-known identy $\cosh^2\phi-\sinh^2\phi=1$, we find $\cosh\phi=\frac{1}{\sqrt{1-v^2}}$. Therefore, \eqref{eq:boost1} can be written in terms of $t,x,t’,x’,v$ as
\begin{equation}
\begin{aligned}
t’&=\frac{t-vx}{\sqrt{1-v^2}}\\
x’&=\frac{x-vt}{\sqrt{1-v^2}}
\end{aligned}\label{eq:boost2}
\end{equation}
Remember that we assumed the speed of light to be $c=1$ for simplicity. For the real $c$ value \eqref{eq:boost2} turns into
\begin{equation}
\begin{aligned}
t’&=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}\\
x’&=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}
\end{aligned}\label{eq:boost3}
\end{equation}
In physics textbooks, \eqref{eq:boost3} is introduced as the Lorentz transformation. If $v\ll c$ meaning $v$ is significantly slower than the speed of light (such a motion is called a non-relativistic motion), \eqref{eq:boost3} is effectively the Galilean transformation
\begin{equation}
\begin{aligned}
t’&=t\\
x’&=x-vt
\end{aligned}\label{eq:galilean}
\end{equation}
for Newtonian mechanics in Euclidean space. $t’=t$ means that time is independent of the relative motion of different observers and we already know this is the case of Newtonian mechanics. The Galilean transformation \eqref{eq:galilean} can be also obtained by taking the limit $c\to \infty$. This indicates that in Newtonian mechanics the speed of light is presumed to be infinity.