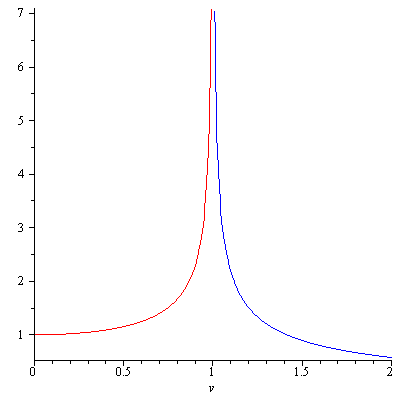
In this note, we obtain the energy-momentum relation \begin{equation}\label{eq:e-m2}E^2=p^2c^2+m_0c^4\end{equation} which was first introduced by P.A.M. Dirac. Before we get to that, let us study some basic quantities of mechanics in special relativity. Suppose the world vector $\vec{r}=(ct,x,y,z)$ is timelike. Then $$dr^2=-c^2dt^2+dx^2+dy^2+dz^2<0$$ Define $d\tau:=\sqrt{-\frac{dr^2}{c^2}}$. Then \begin{equation}\label{eq:proptime}d\tau=\sqrt{1-\frac{v^2}{c^2}}dt\end{equation} $d\tau$ is the actual time measured by the clock in the moving system at the speed $v$. At rest ($v=0$), $d\tau$ coincides with the coordinate time $dt$. $d\tau$ is called the proper time of the moving frame. The derivative of the world vector $\vec{r}=(ct,x,y,z)$ with respect to the proper time $\tau$ is called the four-velocity $$\vec{v}=\frac{d\vec{r}}{d\tau}=\left(c\frac{dt}{d\tau},\frac{dx}{d\tau},\frac{dy}{d\tau},\frac{dz}{d\tau}\right)$$ Using \eqref{eq:proptime}, the four-velocity can be written as \begin{equation}\label{eq:4-velocity}\vec{v}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}(c,{\bf v})\end{equation} where ${\bf v}=\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)$. $$\vec{v}\cdot\vec{v}=\frac{1}{1-\frac{v^2}{c^2}}(-c^2+v^2)=-c^2$$ The four-momentum $\vec{p}$, as a natural generalization of the Newtonian momentum, is defined by \begin{equation}\label{eq:4-momentum}\vec{p}:=m_0\vec{v}=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}(c,{\bf v})\end{equation} $$\vec{p}\cdot\vec{p}=-m_0^2c^2$$ On the other hand, $\vec{p}$ also can be written as \begin{equation}\label{eq:4-momentum2}\vec{p}=(mc,m{\bf v})=\left(\frac{E}{c},{\bf p}\right)\end{equation} where $m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$ and ${\bf p}=(p_x,p_y,p_z)$.

Remark. It is customary in physics literature to write the world vector as $(ict,x,y,z)$ while keeping the metric of spacetime in the appearance of Euclidean metric as seen in [1]. Likewise, the four-momentum is written as $\vec{p}=\left(i\frac{E}{c},{\bf p}\right)$. I am a geometer, not a physicist and I don’t personally like such convention so I am not using it.

Now, from \eqref{eq:4-momentum} and \eqref{eq:4-momentum2}, we obtain the energy-momentum relation \eqref{eq:e-m2}. At rest (${\bf p}=0$), we retrieve Einstein’s famous mass-energy equivalence $E=m_0c^2$. The energy-momentum relation \eqref{eq:e-m2} leads to two very important equations in relativistic quantum mechanics, the Klein-Gordon equation for charged spin-0 particles and the Dirac equation for spin-1/2 fermions [2].

Analogous to the Newtonian force, the four-force is defined by $$\vec{F}=\frac{d\vec{p}}{d\tau}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\frac{d\vec{p}}{dt}$$

Food for thought: For a tachyon, the energy-momentum relation is given by $$E^2=p^2c^2-m_0^2c^4$$ as its rest mass is purely imaginary. Can we obtain a physically sound equation for tachyons from this energy-momentum relation?

References:

[1] Walter Greiner, Classical Mechanics, Point Particles and Relativity, Spinger-Verlag, 2004

[2] Walter Greiner, Relativistic Quantum Mechanics, 3rd Edition, Springer-Verlag, 2000

This is a guest post by Dr. Lawrence R. Mead. Dr. Mead is a Professor Emiritus of Physics at the University of Southern Mississippi.

It is often stated in elementary books and repeated by many that the reason that an object with mass cannot achieve or exceed the speed of light in vacuum is the “mass becomes infinite”, or “time stops” or even “the object has zero size”. There are correct viewpoints for why matter or energy or any signal of any kind cannot exceed light speed and these reasons have little to do directly with mass changes or time dilations or Lorentz contractions.

Reason Number One

Consider a signal of any kind (mass, energy or just information) which travels at speed $u=\alpha c$ beginning at point $x_A$ at time $t=0$ and arriving at position $x_B$ at later time $t>0$. From elementary kinematics,
$$t=(x_B -x_A)/u = {\Delta x \over \alpha c}.$$
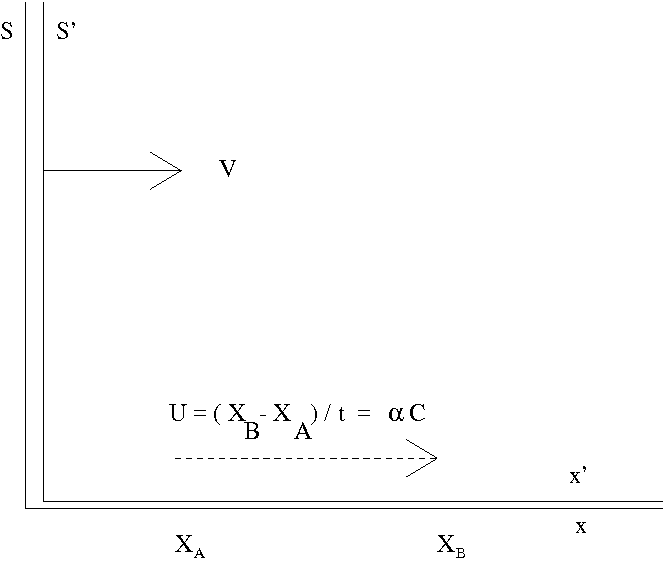Now suppose the signal travels at a speed exceeding $c$, that is $\alpha > 1$. Let us calculate the elapsed time as measured by a frame going by at speed $V<c$. According to the Lorentz transformation,
\begin{equation}\label{eqno1}t’ = \gamma (t-{Vx \over c^2}),\end{equation} where $\gamma=\frac{1}{\sqrt{1-\frac{V^2}{c^2}}}$.
There are two events: the signal leaves $x=x_A$ at $t=0$, and the signal arrives at $x=x_B$ at time $t=\Delta t$. According to \eqref{eqno1}, these events in the moving frame happen at times,
$$t’_A=\gamma ( 0 -Vx_A/c^2)$$ and
$$t’_B=\gamma (\Delta t – Vx_B/c^2).$$
Thus, the interval between events in the moving frame is, \begin{equation}\begin{aligned}\Delta t’ &= t’_B-t’_A\\
&=\gamma \Delta t -\gamma \frac{V}{c^2}(x_B-x_A)\\
&=\gamma \Delta t ( 1-\alpha V/ c).\end{aligned}\label{eqno2}\end{equation}
Now suppose that $\alpha V/c > 1$, which implies that,
$$ c > V > c/\alpha .$$ Then for moving frames within that range of speeds it follows from \eqref{eqno2} that,
$$\Delta t’= t’_B-t’_A <0,$$ meaning physically that the signal arrived before it was sent! This is a logical paradox which is impossible on physical grounds; no one will argue that in any frame a person can be shot before the gun is fired, or you obtain the knowledge of the outcome of a horse race before the race has begun.

Well now what if the two events at $x_A$ and $x_B$ are not causally connected but one (say at $x_B$ for definiteness) simply happened after the other? How does the above argument change? How does the above math “know” that there is or is not a causal connection between the events? Everything goes the same up to the second line of equation \eqref{eqno2}:
\begin{equation}\label{eqno3} \Delta t’ = \gamma \{ \Delta t – V(x_B-x_A)/c^2 \}. \end{equation}
Can there be a moving frame of speed $V<c$ for which the event at $x_B$ (the later one in S) happens before the event at $x_A$ (the earlier one in S)? If so, $\Delta t’ < 0$; from \eqref{eqno3} then we find,
$$\Delta t – V(x_B-x_A)/c^2 < 0, $$ or solving for $V$,
$$ c > V > c{c\over \Delta x/ \Delta t}.$$ In order for $V$ to be less
than $c$, it must therefore be that, ${c\over \Delta x /\Delta t} < 1$, or
$${\Delta x \over \Delta t} > c.$$ This is possible for sufficiently large $\Delta x$ and/or sufficiently small $\Delta t$ because the ratio ${\Delta x \over \Delta t}$ is not the velocity of any signal, though it has the units of speed.

What is the Speed of “Light” Anyway?

Note that the Lorentz transformation contains the speed $c$ in it. What is this speed? Without referencing Maxwell’s equations of Electromagnetism, one does not know that $c$ is in fact the speed of light itself. But the above analysis shows – without reference to Maxwell – that the speed $c$ cannot be exceeded. And what is the speed talked about in the previous discussion? Well, it is the maximum speed at which one event can influence another with given (fixed) separation – thus, $c$ above isn’t really the speed of light at all; rather it is the speed of causality!

Reason Number Two

Imagine, for example, a constant force $F$ acting on a particle of (rest) mass $m$. Newton’s second Law in its relativistic form gives,
\begin{equation}\begin{aligned} F &= {dp \over dt} \\
&= {d \over dt} \, mv\gamma \\
&= m \gamma^3 \, \dot v, \end{aligned}\label{eqno4}\end{equation}
where we have assumed straight line motion. This is an autonomous differential equation whose solution, assuming the object is initially at rest, is,
$$ v(t)=at/(1+a^2t^2/c^2)^{1/2}, $$
where $a=F/m$. It is clear that as $t \to \infty$, $v(t)$
approaches $c$ and not infinity. Moreover, the differential impulse at arbitrary time $t$ on the particle can be found from taking the derivative of $v(t)$ given in the last equation,
\begin{equation}\label{eqno5}m\, dv = { F \, dt \over (1+a^2t^2/c^2)^{3/2}}. \end{equation}
From equation \eqref{eqno5}, it is clear that the incremental speed increase $dv$ over time $dt$ approaches zero as $t \to \infty$. Thus, from this point of view we see that while the force still does work, the increase in speed for a given interval of time and incremental amount of work, is less and less as time goes on which is why the speed never reaches $c$ over any finite time interval.

Reason Number Three

In the interval of time $dt$ as measured in some inertial frame observing a moving body, the clock attached to the body ticks off proper time
\begin{equation}\label{eqno6}d\tau = \sqrt{1-v^2/c^2}\, dt. \end{equation}
However, for light $v\equiv c$, and therefore $d\tau\equiv 0$. Light takes no proper time to go between two points however distantly separated in space. Thus, no object could travel faster than taking no time. This is the oft-repeated mantra of textbooks, and, while the mathematics verifies it, there are far more fundamental reasons, the best being causality as outlined above.

Often you hear that Einstein’s relativity prevents FTL (Faster-Than-Light). Is that true? The answer is yes and no. It is not possible for a spaceship to travel faster than the speed of light. But there may be a particle that travels FTL and the existence of such a particle would not violate the principles of relativity if its speed already exceeds the speed of light when it is created. The hypothetical particle that travels FTL is called a tachyon. (tachys means fast in Greek) The name was coined by a Columbia University physicist Gerald Feinberg in 1967. When he was asked why he thought about such a particle Feinberg reportedly quoted a Jewish proverb “Everything which is not forbidden is allowed.” (Author’s note: This is from something I read more than 3 decades ago when I was a high school student so I cannot cite its source. Also I could not find any such Jewish proverb either. It is however a constitutional principle of English law.)

For a Tachyon, the Lorentz transformation is given by the complex coordinates \begin{align*}t’&=-i\frac{t-\frac{v}{c^2}x}{\sqrt{\frac{v^2}{c^2}-1}}\\x’&=-i\frac{x-vt}{\sqrt{\frac{v^2}{c^2}-1}}\end{align*} where $i=\sqrt{-1}$. Although this is a complex transformation, it is still an isometry i.e. it preserves the Minkowski metric. In order for its energy $E$ to be real one has to assume that its rest mass is purely imaginary $im_0$ where $m_0>0$ is real and hence from the relativistic energy $$E=\frac{im_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{im_0c^2}{i\sqrt{\frac{v^2}{c^2}-1}}=\frac{m_0c^2}{\sqrt{\frac{v^2}{c^2}-1}}$$ Imaginary rest mass may sound weird but rest mass is not an observable because a particle is never at rest. What’s important is energy being real as it is an observable. The following figure shows energies of a subluminal particle (in red) and a superluminal particle (in blue) with $m_0=c=1$).

Properties of Tachyons:

1. The speed of light $c$ is the greatest lower bound of Tachyon’s speed. There is no upper limit of Tachyon’s speed.
2. Tachyons have imaginary rest mass (as we discussed above).
3. In order for a tachyon to slow down to the speed of light, it requires infinite amount of energy and momentum.
4. Another peculiar nature of tachyons. If a tachyon looses energy, its speed increases. At $E=0$, $v=\infty$.

How do we detect tachyons if they exist? Since tachyons travel FTL, we can’t see them coming. However if they are charged particles, they will emit electromagnetic Mach shock waves called Tscherenkov (also spelled Cherenkov) radiations. This always happens when charged particles are passing through a medium with a higher speed than the phase speed of light in the medium. By detecting such Tscherenkov radiations we may be able to confirm the existence of tachyons.

An interesting question is “can we use tachyons for FTL communications? ” It was answered by Richard C. Tolman as negative in his book [2] (pp 54-55). In [2]. Tolman considered the following thought experiment. Suppose a signal is being sent from a point $A$ (cause) to another point $B$ (effect) with speed $u$. In an inertial frame $S$ where $A$ and $B$ are at rest, the time of arrival at $B$ is given by $$\Delta t=t_B-t_A=\frac{B-A}{u}$$ In another inertial frame $S’$ moving with speed $v$ relative to $S$ the time of arrival at $B$ is given, according to the Lorentz transformation, by \begin{align*}\Delta t’&=t’_{B}-t’_{A}\\&=\frac{t_B-\frac{v}{c^2}x_B}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{t_A-\frac{v}{c^2}x_A}{\sqrt{1-\frac{v^2}{c^2}}}\\&=\frac{1-u\frac{v}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}\Delta t\end{align*} If $u>c$ then certain values of $v$ can make $\Delta t’$ negative. In other words, the effect occurs before the cause in this frame, the violation of causality!

Food for Thought: Can one possibly use tachyons to send a message (signal) to the past?

References:

1. Walter Greiner, Classical Mechanics, Point Particles and Relativity, Springer, 2004
2. Richard C. Tolman, The Theory of the Relativity of Motion, University of California Press, 1917. A scanned copy is available for viewing online here.

In this note, we discuss one of the relativistic effects called Time Dilation namely a clock that is moving relative to an observer will be measured to tick slower than a clock that is at rest in the observer’s reference frame. This is pretty intriguing for those who are familiar with Newtonian notion of time as being a universal parameter for motions. Let us do a thought experiment. Let us consider a frame $K$ at rest and suppose that a light ray is emitted by the light source $Q$ and after reflection by the mirror $S$ is received at $E$. See Figure 1.

Figure 1. Time Dilation

The measured time interval in the frame $K$ is $\Delta t=t_2-t_1=\frac{2l}{c}$. Now consider a frame $K’$ moving at a constant speed $v$ to the right. An observer at rest in $K’$ sees the light ray emerging from $Q$, hitting the mirror (at rest in $K$) at $M$ and reaching the $x’$-axis again at $E$. The observer measures a longer time interval as the light has to travel a longer path to reach the receiver but the speed of light is remained the same according to Einstein’s postulate. How much longer? The time $\Delta t’$ measured by an observer at rest in the frame $K’$ can be easily calculated using the Pythagorean law applied to the isosceles triangle seen in Figure 1. We find
$$\left(\frac{c\Delta t’}{2}\right)^2=l^2+\left(\frac{v\Delta t’}{2}\right)$$
Solving this for $\Delta t’$ we find
\begin{equation}
\label{eq:timedilation}
\Delta t’=\frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}
\end{equation}
Note that \eqref{eq:timedilation} amounts to the Lorentz transformation into the system $K’$
$$\Delta t’=t_2′-t_1′,$$
where
$$t_i’=\frac{t_i-\frac{v}{c^2}x_i}{\sqrt{1-\frac{v^2}{c^2}}},\ i=1,2$$
Since $x_1=x_2$, we obtain \eqref{eq:timedilation}. In case this whole frame thing is confusing, let us imagine that you are sitting in a train that is running at a constant speed. Since there is no acceleration, you do not feel that you are moving. So inside the train you are at rest (frame $K$). For an observer outside you are moving (frame $K’$) and the observer would measure the time ($\Delta t’$) on your clock ticking slower than what you would measure it ($\Delta t$). In physics $\Delta t$ is called proper time. Simply speaking proper time is the time measured by a clock that is moving along with inertial frame. Mathematically, proper time can be calculated from the arc length $ds^2$ of a worldline, the trajectory of a moving particle or an object in spacetime. Denote by $\tau$ the proper time. Then since the worldline is timelike (meaning leaning more toward time), $ds^2=-c^2d\tau^2$. So the proper time interval is given by
\begin{equation}
\begin{aligned}
\Delta\tau&=\frac{1}{c}\int\sqrt{-ds^2}\\
&=\frac{1}{c}\int\sqrt{c^2dt^2-dx^2-dy^2-dz^2}\\
&=\int\sqrt{1-\frac{v(t)^2}{c^2}}dt
\end{aligned}\label{eq:propertime}
\end{equation}
If $v(t)$ is constant speed $v$, \eqref{eq:propertime} becomes \eqref{eq:timedilation}.
The time dilation effect in \eqref{eq:timedilation} hints us that a time travel to the future may be possible. Here is how. The exoplanet Proxima b is interesting because it is orbiting within the habitable zone of the red dwarf star Proxima Centauri which is a part of triple star system Alpha Centauri in the Constellation of Centaurus, and also because it is relatively close to our world. It is located about 4.2 light-years or 40 trillion km from Earth. In fact, it is the closest known exoplanet to the Solar System.

Artist’s depiction of Proxima b

Let us say we are sending a manned spaceship to Proxima b. Also let us assume that the spaceship can travel at 90% of the speed of light. (It is actually impossible to achieve this due to a physical limitation. I will discuss this in my other note at a later time. In reality, the best we can achieve using nuclear propulsion is about 0.067% of the speed of light.) For people on Earth it would take $\Delta t’=\frac{4\times 10^{13}\mbox{km}}{2.7\times 10^5\mbox{km/sec}}=1.\overline{481}\times 10^8\mbox{sec}$ for the spaceship to get to Proxima b. Since $1\mbox{sec}=3.17\times 10^{-8}\mbox{years}$, it is 4.7 years. Since it would take the same time from Proxima b to Earth, the overall travel time for people on Earth is 9.4 years. In reality, we will have to take some factors into consideration: it takes time for the spaceship to accelerate to reach 90% of the speed of light, once the spaceship is near Proxima b it will have to slow down for stopping or U-turning, etc. But for the sake of simplicity we will disregard those factors. For the crew memebers it took only
\begin{align*}
\Delta t&=\sqrt{1-\frac{v^2}{c^2}}\Delta t’\\
&=\sqrt{1-(0.9)^2}\cdot 1.\overline{481}\times 10^8\mbox{sec}\\
&\approx 0.65\times 10^8\mbox{sec}\\
&\approx 2\mbox{yrs}
\end{align*}
to get to Proxima b. So when they come back home, it’s like they traveled more then 5 years forward in time. I know it is not what you probably think and yes I admit that this is a kind of boring time travel. Can one travel backward in time? This is one of the most intriguing questions. I will come back to this question at another time.

I will finish this note with an example as an application of \eqref{eq:timedilation}. This example was taken from [1].

Example. Muon Decay

The Earth is surrounded by an atmosphere of about 30 km thickness screening us off from cosmic radiation. If a proton from the consmic radiation hits the atmosphere, $\pi$-mesons are produced and several of them decay further into a muon and a neutrino. The muon has a mean lifetime of $\Delta t=2\times 10^{-6}\mbox{sec}$ in its rest system. Classically it would travel even with the speed of light (only massless particles can travel at the speed of light)
\begin{align*}
s&=c\Delta t\\
&=3\times 10^5\mbox{km/sec}\cdot 2\times 10^{-6}\mbox{sec}\\
&=0.6\mbox{km}
\end{align*}
or 600m. If this were true, muon particles would never reach the surface, but they are detected on the surface. In the relativistic approach,
$$s’=v\Delta t’=\frac{v\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}$$
Muons at rest have a mass of $m_0c^2=10^8$eV (I know it is actually energy but due to mass-energy equivalence physicists customarily call it mass.) The cosmic muons are created at an altitude of about 10km with a total energy of $E=5\times 10^9$eV. In order to apply this information we rewite $S’$ as
\begin{align*}
S’&=\frac{vm_0c^2}{m_0c^2\sqrt{1-\frac{v^2}{c^2}}}\Delta t\\
&=\frac{v}{m_0c^2}E\Delta t\\
&\leq\frac{c}{m_0c^2}E\Delta t\\
&=\frac{3\times 10^5\mbox{km/sec}}{10^8\mbox{eV}}\cdot 5\times 10^9\mbox{eV}\cdot 2\times 10^{-6}\mbox{sec}\\
&=30\mbox{km}
\end{align*}
Here we used $E=mc^2=\frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}$. We will discuss this later in another post. The actual measurement gives a value of 38km.

References:

[1] Walter Greiner, Classical Mechanics, Point Particles and Relativity, Springer, 2004

[2] Paul A. Tipler and Ralph A. Llewellyn, Modern Physics, 5th Edition, W. H. Freeman and Company, 2008

Relativistic equations are the equations whose solutions describe certain relativistic motions. Such equations include wave equation, Klein-Gordon equation, Dirac equation etc. A relativistic equation must describe the same physical motion independent of frames i.e. whether an observer is in a frame at rest or in a frame moving at the constant speed $v$. For this reason, all those relativistic equations are required to be invariant under the Lorentz transformation. We show that the wave equation
\begin{equation}
\label{eq:waveeq}
-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=0
\end{equation}
is Lorentz invariant. Here we consider only 1-dimensional wave equation for simplicity. Wave equation has two kinds of solutions. Given boundary conditions its solution describes a vibrating string in which case the boundary conditions are the ends of the string that are held fixed. This is called Fourier’s solution. The other type can be obtained by not imposing any boundary conditions. The resulting solution would describe a propagating wave in vacuum spacetime. Such a propagating wave includes electromagnetic waves. Light is also an electromagnetic wave. This is called a d’Alembert’s solution. The proof is easy. All that’s required is the chain rule.

First let us recall the Lorenz transformation
$$t’=\frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}},\ x’=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$$
Using the chain rule we find
\begin{align*}
\frac{\partial}{\partial x}&=\frac{\partial}{\partial x’}\frac{\partial x’}{\partial x}+\frac{\partial}{\partial t’}\frac{\partial t’}{\partial x}\\
&=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial x’}-\frac{v}{c^2\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial t’}\\
\frac{\partial}{\partial t}&=\frac{\partial}{\partial x’}\frac{\partial x’}{\partial t}+\frac{\partial}{\partial t’}\frac{\partial t’}{\partial t}\\
&=-\frac{v}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial x’}+\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\frac{\partial}{\partial t’}
\end{align*}
Applying the chain rule again,
\begin{align*}
\frac{\partial^2}{\partial x^2}&=\frac{1}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {x’}^2}+\frac{v^2}{c^4\left(1-\frac{v^2}{c^2}\right)}\frac{\partial^2}{\partial {t’}^2}-2\frac{v}{c^2\left(1-\frac{v^2}{c^2}\right)}\frac{\partial^2}{\partial t’\partial x’}\\
\frac{\partial^2}{\partial t^2}&=\frac{v^2}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {x’}^2}+\frac{1}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial {t’}^2}-2\frac{v}{1-\frac{v^2}{c^2}}\frac{\partial^2}{\partial t’\partial x’}
\end{align*}
It follows that
$$-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=-\frac{1}{c^2}\frac{\partial^2\psi}{\partial {t’}^2}+\frac{\partial^2\psi}{\partial {x’}^2}$$
Therefore, the wave equation is Lorentz invariant.

Would the wave equation be invariant under the Galilean transformation? The answer is no. Recall the Galilean transformation
$$t’=t,\ x’=x-vt$$
We find that under the Galiean transformation
$$-\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}+\frac{\partial^2\psi}{\partial x^2}=-\frac{1}{c^2}\frac{\partial^2\psi}{\partial {t’}^2}+\left(1-\frac{v^2}{c^2}\right)\frac{\partial^2\psi}{\partial {x’}^2}+\frac{2v}{c^2}\frac{\partial^2\psi}{\partial t’\partial x’}$$
Hence obvisouly the wave equation is not invariant under the Galiean transformation. This implies that there is no light in Euclidean space.

Food for Thought. You can also show that the heat equation (1-dimensional)
$$-\frac{\partial u}{\partial t}+\alpha\frac{\partial^2 u}{\partial x^2}=0$$
is not Lorentz invariant. Is there any relativistic version of the heat equation? There are models of relativistic heat conduction but in my opinion they are more like mathematically augmented equations rather than they are derived in a physically meaningful way. So my question is can we derive a physically meaningful equation of relativistic heat conduction? One may wonder if there is actually any physical phenomenon that exhibits a relativistic heat conduction. As far as I know there isn’t any observed one yet. I speculate though that one may observe a relativistic heat conduction from an extreme physical phenomenon such as a quasar jet.

Update: Of course the Lorentz invariance can be also shown using the Lorentz transformation \begin{align*}t’&=\cosh\phi t-\sinh\phi x\\x’&=-\sinh\phi t+\cosh\phi x\end{align*}

Update: For 3-dimensional case the wave equation is given by $$\Box\psi=0$$
where $\Box=-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}+\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$ is the d’Alembert’s operator. This case is actually simpler to show its Lorentz invariance. Note $\Box=\nabla\cdot \nabla$ where $\nabla=\frac{1}{c}\frac{\partial}{\partial t}\hat e_0+\frac{\partial}{\partial x}\hat e_x+\frac{\partial}{\partial y}\hat e_2+\frac{\partial}{\partial z}\hat e_3$. Since $\nabla$ is a 4-vector (rigorously it is not a vector but an operator but can be treated as a vector), its squared norm $\Box$ has to be Lorentz invariant.