In this note, we discuss one of the relativistic effects called Time Dilation namely a clock that is moving relative to an observer will be measured to tick slower than a clock that is at rest in the observer’s reference frame. This is pretty intriguing for those who are familiar with Newtonian notion of time as being a universal parameter for motions. Let us do a thought experiment. Let us consider a frame $K$ at rest and suppose that a light ray is emitted by the light source $Q$ and after reflection by the mirror $S$ is received at $E$. See Figure 1.

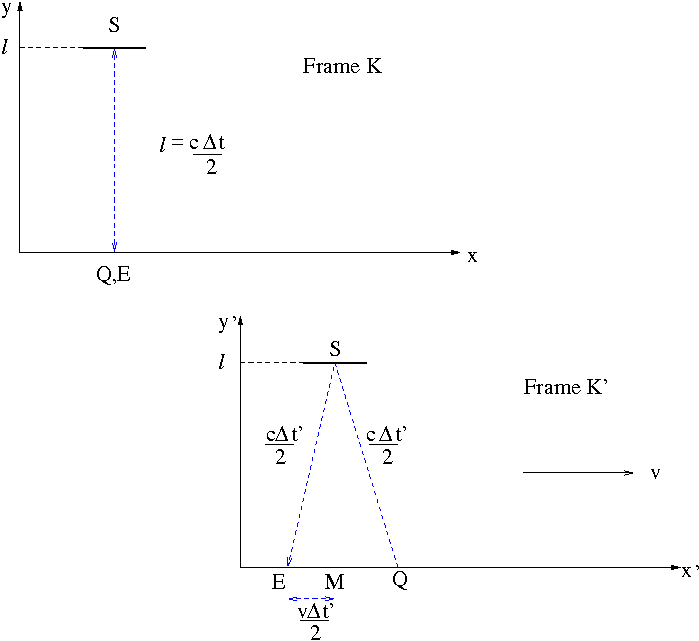
Figure 1. Time Dilation

The measured time interval in the frame $K$ is $\Delta t=t_2-t_1=\frac{2l}{c}$. Now consider a frame $K’$ moving at a constant speed $v$ to the right. An observer at rest in $K’$ sees the light ray emerging from $Q$, hitting the mirror (at rest in $K$) at $M$ and reaching the $x’$-axis again at $E$. The observer measures a longer time interval as the light has to travel a longer path to reach the receiver but the speed of light is remained the same according to Einstein’s postulate. How much longer? The time $\Delta t’$ measured by an observer at rest in the frame $K’$ can be easily calculated using the Pythagorean law applied to the isosceles triangle seen in Figure 1. We find
$$\left(\frac{c\Delta t’}{2}\right)^2=l^2+\left(\frac{v\Delta t’}{2}\right)$$
Solving this for $\Delta t’$ we find
\begin{equation}
\label{eq:timedilation}
\Delta t’=\frac{\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}
\end{equation}
Note that \eqref{eq:timedilation} amounts to the Lorentz transformation into the system $K’$
$$\Delta t’=t_2′-t_1′,$$
where
$$t_i’=\frac{t_i-\frac{v}{c^2}x_i}{\sqrt{1-\frac{v^2}{c^2}}},\ i=1,2$$
Since $x_1=x_2$, we obtain \eqref{eq:timedilation}. In case this whole frame thing is confusing, let us imagine that you are sitting in a train that is running at a constant speed. Since there is no acceleration, you do not feel that you are moving. So inside the train you are at rest (frame $K$). For an observer outside you are moving (frame $K’$) and the observer would measure the time ($\Delta t’$) on your clock ticking slower than what you would measure it ($\Delta t$). In physics $\Delta t$ is called proper time. Simply speaking proper time is the time measured by a clock that is moving along with inertial frame. Mathematically, proper time can be calculated from the arc length $ds^2$ of a worldline, the trajectory of a moving particle or an object in spacetime. Denote by $\tau$ the proper time. Then since the worldline is timelike (meaning leaning more toward time), $ds^2=-c^2d\tau^2$. So the proper time interval is given by
\begin{equation}
\begin{aligned}
\Delta\tau&=\frac{1}{c}\int\sqrt{-ds^2}\\
&=\frac{1}{c}\int\sqrt{c^2dt^2-dx^2-dy^2-dz^2}\\
&=\int\sqrt{1-\frac{v(t)^2}{c^2}}dt
\end{aligned}\label{eq:propertime}
\end{equation}
If $v(t)$ is constant speed $v$, \eqref{eq:propertime} becomes \eqref{eq:timedilation}.
The time dilation effect in \eqref{eq:timedilation} hints us that a time travel to the future may be possible. Here is how. The exoplanet Proxima b is interesting because it is orbiting within the habitable zone of the red dwarf star Proxima Centauri which is a part of triple star system Alpha Centauri in the Constellation of Centaurus, and also because it is relatively close to our world. It is located about 4.2 light-years or 40 trillion km from Earth. In fact, it is the closest known exoplanet to the Solar System.

Artist’s depiction of Proxima b

Let us say we are sending a manned spaceship to Proxima b. Also let us assume that the spaceship can travel at 90% of the speed of light. (It is actually impossible to achieve this due to a physical limitation. I will discuss this in my other note at a later time. In reality, the best we can achieve using nuclear propulsion is about 0.067% of the speed of light.) For people on Earth it would take $\Delta t’=\frac{4\times 10^{13}\mbox{km}}{2.7\times 10^5\mbox{km/sec}}=1.\overline{481}\times 10^8\mbox{sec}$ for the spaceship to get to Proxima b. Since $1\mbox{sec}=3.17\times 10^{-8}\mbox{years}$, it is 4.7 years. Since it would take the same time from Proxima b to Earth, the overall travel time for people on Earth is 9.4 years. In reality, we will have to take some factors into consideration: it takes time for the spaceship to accelerate to reach 90% of the speed of light, once the spaceship is near Proxima b it will have to slow down for stopping or U-turning, etc. But for the sake of simplicity we will disregard those factors. For the crew memebers it took only
\begin{align*}
\Delta t&=\sqrt{1-\frac{v^2}{c^2}}\Delta t’\\
&=\sqrt{1-(0.9)^2}\cdot 1.\overline{481}\times 10^8\mbox{sec}\\
&\approx 0.65\times 10^8\mbox{sec}\\
&\approx 2\mbox{yrs}
\end{align*}
to get to Proxima b. So when they come back home, it’s like they traveled more then 5 years forward in time. I know it is not what you probably think and yes I admit that this is a kind of boring time travel. Can one travel backward in time? This is one of the most intriguing questions. I will come back to this question at another time.

I will finish this note with an example as an application of \eqref{eq:timedilation}. This example was taken from [1].

Example. Muon Decay

The Earth is surrounded by an atmosphere of about 30 km thickness screening us off from cosmic radiation. If a proton from the consmic radiation hits the atmosphere, $\pi$-mesons are produced and several of them decay further into a muon and a neutrino. The muon has a mean lifetime of $\Delta t=2\times 10^{-6}\mbox{sec}$ in its rest system. Classically it would travel even with the speed of light (only massless particles can travel at the speed of light)
\begin{align*}
s&=c\Delta t\\
&=3\times 10^5\mbox{km/sec}\cdot 2\times 10^{-6}\mbox{sec}\\
&=0.6\mbox{km}
\end{align*}
or 600m. If this were true, muon particles would never reach the surface, but they are detected on the surface. In the relativistic approach,
$$s’=v\Delta t’=\frac{v\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}$$
Muons at rest have a mass of $m_0c^2=10^8$eV (I know it is actually energy but due to mass-energy equivalence physicists customarily call it mass.) The cosmic muons are created at an altitude of about 10km with a total energy of $E=5\times 10^9$eV. In order to apply this information we rewite $S’$ as
\begin{align*}
S’&=\frac{vm_0c^2}{m_0c^2\sqrt{1-\frac{v^2}{c^2}}}\Delta t\\
&=\frac{v}{m_0c^2}E\Delta t\\
&\leq\frac{c}{m_0c^2}E\Delta t\\
&=\frac{3\times 10^5\mbox{km/sec}}{10^8\mbox{eV}}\cdot 5\times 10^9\mbox{eV}\cdot 2\times 10^{-6}\mbox{sec}\\
&=30\mbox{km}
\end{align*}
Here we used $E=mc^2=\frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}}$. We will discuss this later in another post. The actual measurement gives a value of 38km.

References:

[1] Walter Greiner, Classical Mechanics, Point Particles and Relativity, Springer, 2004

[2] Paul A. Tipler and Ralph A. Llewellyn, Modern Physics, 5th Edition, W. H. Freeman and Company, 2008