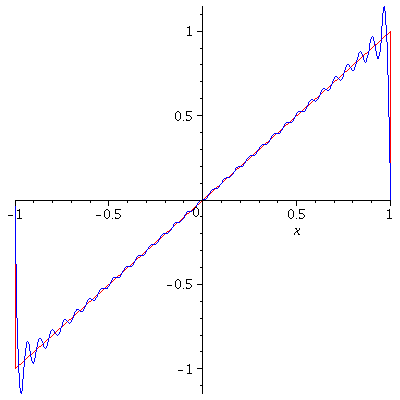
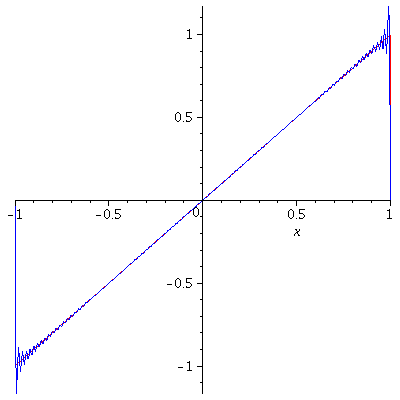
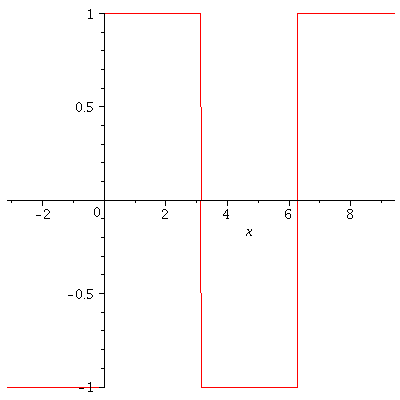
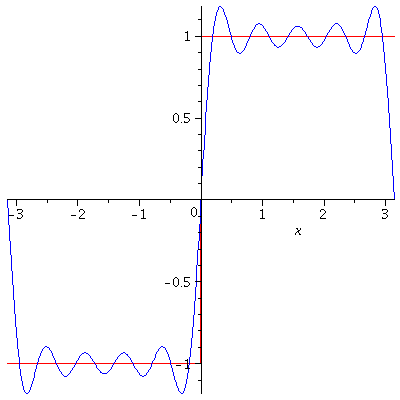
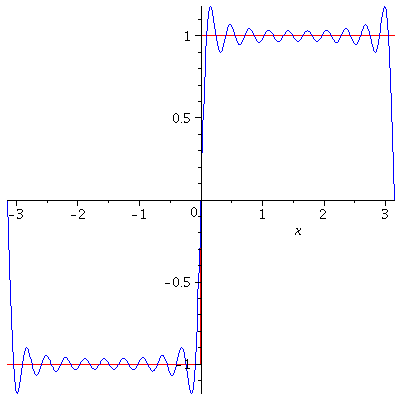
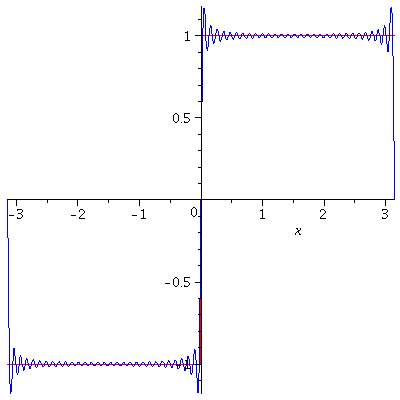
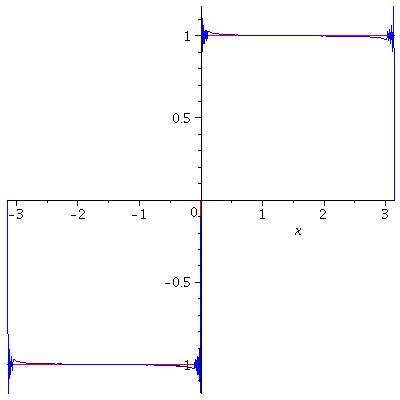
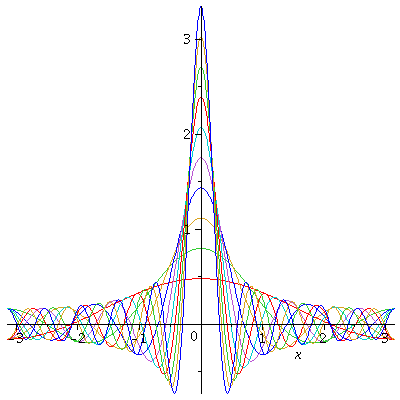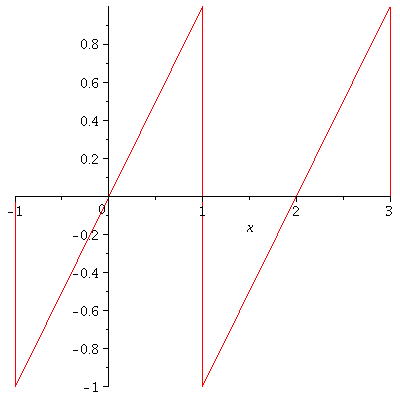In here, we have seen that if a function $f$ is Riemann integrable on every bounded interval, it can be expended as a trigonometric series called a Fourier series by assuming that the series converges to $f$. So, it would be natural to pause the following question. If $f$ is a periodic function, would its Fourier series always converge to $f$? The answer is affirmative if $f$ is in addition piecewise smooth.

Let $S_N^f(\theta)$ denote the $n$-the partial sum of the Fourier series of a $2\pi$-periodic function $f(\theta)$. Then
\begin{equation}
\label{eq:partsum}
\begin{aligned}
S_N^f(\theta)&=\sum_{-N}^N c_ne^{in\theta}\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\psi)e^{in(\theta-\psi)}d\psi\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\psi)e^{in(\psi-\theta)}d\psi.
\end{aligned}
\end{equation}
Let $\phi=\psi-\theta$. Then
\begin{align*}
S_N^f(\theta)&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi+\theta}^{\pi+\theta} f(\phi+\theta)e^{in\phi}d\phi\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\phi+\theta)e^{in\phi}d\phi\\
&=\int_{-\pi}^\pi f(\theta+\phi)D_N(\phi)d\phi,
\end{align*}
where
\begin{equation}
\label{eq:dkernel}
\begin{aligned}
D_N(\phi)&=\frac{1}{2\pi}\sum_{-N}^N e^{in\phi}\\
&=\frac{1}{2\pi}\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}\\
&=\frac{1}{2\pi}\frac{\sin\left(N+\frac{1}{2}\right)\phi}{\sin\frac{1}{2}\phi}.
\end{aligned}
\end{equation}
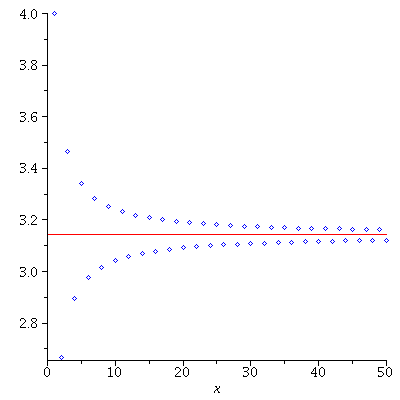
$D_N(\phi)$ is called the $N$-th Dirichlet kernel. Note that the Dirichlet kernel can be used to realize the Dirac delta function $\delta(x)$, i.e.
$$\delta(x)=\lim_{n\to\infty}\frac{1}{2\pi}\frac{\sin\left(n+\frac{1}{2}\right)x}{\sin\frac{1}{2}x}.$$

Note that
$$\frac{1}{2}+\frac{\sin\left(N+\frac{1}{2}\right)\theta}{2\sin\frac{1}{2}\theta}=1+\sum_{n=1}^N\cos n\theta\ (0<\theta<2\pi)$$
Using this identity, one can easily show that:

Lemma. For any $N$,
$$\int_{-\pi}^0 D_N(\theta)d\theta=\int_0^{\pi}D_N(\theta)d\theta=\frac{1}{2}.$$

Now, we area ready to prove the following convergence theorem.

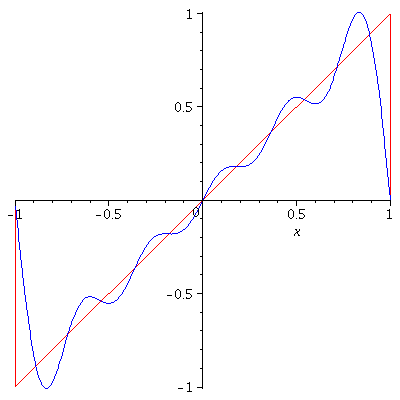
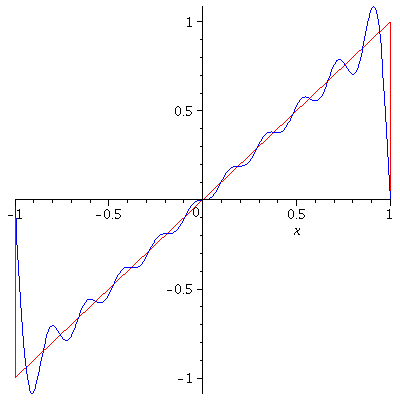
Theorem. If $f$ is $2\pi$-periodic and piecewise smooth on $\mathbb{R}$, then
$$\lim_{N\to\infty} S_N^f(\theta)=\frac{1}{2}[f(\theta-)+f(\theta+)]$$
for every $\theta$. Here, $f(\theta-)=\lim_{\stackrel{h\to 0}{h>0}}f(\theta-h)$ and $f(\theta+)=\lim_{\stackrel{h\to 0}{h>0}}f(\theta+h)$. In particular, $\lim_{N\to\infty}S_N^f(\theta)=f(\theta)$ for every $\theta$ at which $f$ is continuous.

Proof. By Lemma,
$$\frac{1}{2}f(\theta-)=f(\theta-)\int_{-\pi}^0 D_N(\phi)d\phi,\ \frac{1}{2}f(\theta+)=f(\theta+)\int_0^\pi D_N(\phi)d\phi.$$
So,
\begin{align*}
S_N^f(\theta)-\frac{1}{2}[f(\theta-)+f(\theta+)]&=\int_{-\pi}^0[f(\theta+\phi)-f(\theta-)]D_N(\phi)d\phi+\\
&\int_0^\pi[f(\theta+\phi)-f(\theta+)]D_N(\phi)d\phi\\
&=\frac{1}{2\pi}\int_{-\pi}^0[f(\theta+\phi)-f(\theta-)]\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}d\phi\\
&+\frac{1}{2\pi}\int_0^\pi[f(\theta+\phi)-f(\theta+)]\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}d\phi.
\end{align*}
$$\lim_{\phi\to 0+}\frac{f(\theta+\phi)-f(\theta+)}{e^{i\phi}-1}=\frac{f'(\theta+)}{i},\ \lim_{\phi\to 0-}\frac{f(\theta+\phi)-f(\theta-)}{e^{i\phi}-1}=\frac{f'(\theta-)}{i}.$$
Hence, the function
$$g(\phi):=\left\{\begin{aligned}
&\frac{f(\theta+\phi)-f(\theta+)}{e^{i\phi}-1},\ -\pi<\phi<0,\\
&\frac{f(\theta+\phi)-f(\theta-)}{e^{i\phi}-1},\ 0<\phi<\pi
\end{aligned}\right.$$
is piecewise continuous on $[-\pi,\pi]$. By the corollary to Bessel’s inequality,
$$c_n=\frac{1}{2\pi}\int_{-\pi}^\pi g(\phi)e^{in\phi}d\phi\to 0$$
as $n\to\pm\infty$. Therefore,
\begin{align*}
S_N^f(\theta)-\frac{1}{2}[f(\theta-)+f(\theta+)]&=\frac{1}{2\pi}\int_{-\pi}^\pi g(\phi)[e^{i(N+1)\phi}-e^{-iN\phi}]d\phi\\
&=c_{-(N+1)}-c_N\\
&\to 0
\end{align*}
as $N\to\infty$. This completes the proof.

Corollary. If $f$ and $g$ are $2\pi$-periodic and piecewise smooth, and $f$ and $g$ have the same Fourier coefficients, then $f=g$.

Proof. If $f$ and $g$ have the same Fourier coefficients, their their Fourier series are the same. Due to the conditions on $f$ and $g$, the Fourier series of $f$ and $g$ converge to $f$ and $g$ respectively by the above convergence theorem. Hence, $f=g$.

Bessel’s inequality is important in studying Fourier series.

Theorem. If $f$ is $2\pi$-periodic and Riemann integrable on $[-\pi,\pi]$ and if the Fourier coefficients $c_n$ are defined by
$$c_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(\theta)e^{-in\theta}d\theta,$$
then
\begin{equation}
\label{eq:besselinequality}
\sum_{n=-\infty}^\infty|c_n|^2\leq\frac{1}{2\pi}\int_{-\pi}^\pi|f(\theta)|^2d\theta.
\end{equation}

Proof.
\begin{align*}
0&\leq|f(\theta)-\sum_{-N}^Nc_ne^{in\theta}|^2\\
&=f(\theta)^2-\sum_{-N}^Nf(\theta)[c_ne^{in\theta}+\overline{c_n}e^{-in\theta}]+\sum_{m,n=-N}^Nc_m\overline{c_n}e^{i(m-n)\theta}
\end{align*}
By integrating,
\begin{align*}
\frac{1}{2\pi}\int_{-\pi}^\pi|f(\theta)-\sum_{-N}^Nc_ne^{in\theta}|^2d\theta&=\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)^2d\theta-\sum_{-N}^N\left[c_n\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)e^{in\theta}d\theta\right.\\
\left.+\overline{c_n}\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)e^{-in\theta}d\theta\right]+&\sum_{m,n=-N}^Nc_m\overline{c_n}\frac{1}{2\pi}\int_{-\pi}^\pi e^{i(m-n)\theta}d\theta\\
&=\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)^2d\theta-\sum_{-N}^N|c_n|^2.
\end{align*}
Hence, for each $N=1,2,\cdots$,
$$\sum_{-N}^N|c_n|^2\leq\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)^2d\theta.$$
Taking the limit $N\to\infty$, we obtain
$$\sum_{-\infty}^\infty|c_n|^2\leq\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)^2d\theta.$$

Note that $|a_0|^2=4|c_0|^2$, $|a_n|^2+|b_n|^2=2(|c_n|+|c_{-n}|^2)$, $n\geq 1$. So, in terms of the real coefficients, Bessel’s inequality can be written as
\begin{equation}
\label{eq:besselinequality2}
\frac{1}{4}|a_0|^2+\frac{1}{2}\sum_1^\infty(|a_n|^2+|b_n|^2)\leq\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)^2d\theta.
\end{equation}
Bessel’s inequality implies that $\sum|a_n|^2$, $\sum|b_n|^2$, $\sum|c_n|^2$ are convergent and hence the series of Fourier coefficients $\sum a_n$, $\sum b_n$, $\sum c_n$ are convergent. As we studied in undergraduate calculus the following corollary holds then.

Corollary. The Fourier coefficients $a_n$, $b_n$, $c_n$ tend to zero as $n\to\infty$ (and also as $n\to -\infty$ for $c_{-n}$).

Let us recall the Hooke’s law
\begin{equation}
\label{eq:hooke}
F=-kx.
\end{equation}
Newton’s second law of motion is
\begin{equation}
\label{eq:newton}
F=ma=m\ddot{x},
\end{equation}
where $\ddot{x}=\frac{d^2 x}{dt^2}$. The equations \eqref{eq:hooke} and \eqref{eq:newton} result the equation of a simple harmonic oscillator
\begin{equation}
\label{eq:ho}
m\ddot{x}+kx=0.
\end{equation}
Integrating \eqref{eq:ho} with respect to $x$, we have
$$\int(m\ddot{x}dx+kxdx)=E_0,$$
where $E_0$ is a constant. $d\dot{x}=\ddot{x}dt$ and $\dot{x}d\dot{x}=\dot{x}\ddot{x}dt=\ddot{x}dx$. So,
\begin{align*}
\int(m\ddot{x}dx+kxdx)&=\int(m\dot{x}d\dot{x}+kxdx)\\
&=\frac{1}{2}m\ddot{x}+\frac{1}{2}kx^2.
\end{align*}
Hence, we obtain the conservation law of energy
\begin{equation}
\label{eq:energy}
\frac{1}{2}m\ddot{x}+\frac{1}{2}kx^2=E_0.
\end{equation}
The general solution of \eqref{eq:ho} is
\begin{equation}
\label{eq:hosol}
\begin{aligned}
x(t)&=a\cos\omega t+b\sin\omega t\\
&=\sqrt{a^2+b^2}\sin(\omega t+\theta),
\end{aligned}
\end{equation}
where $a$ and $b$ are constants, $\omega=\sqrt{\frac{k}{m}}$ and $\theta=\tan^{-1}\left(\frac{a}{b}\right)$. From \eqref{eq:energy} and \eqref{eq:hosol}, the total energy $E_0$ is computed to be
$$E_0=\frac{1}{2}m\omega^2(a^2+b^2).$$
This tells us that the total energy of a simple harmonic oscillator is proportional to $a^2+b^2$, the squared amplitude. As seen here, the sawtooth function $f(x)$ is represented as the Fourier series
\begin{align*}
f(x)&=-\frac{2L}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{n}\sin\left(\frac{n\pi x}{L}\right)\\
&=\frac{2L}{\pi}\left\{\sin\left(\frac{\pi x}{L}\right)-\frac{1}{2}\sin\left(\frac{2\pi x}{L}\right)+\frac{1}{3}\sin\left(\frac{3\pi x}{L}\right)-\cdots\right\}.
\end{align*}
The amplitude $c_n=\frac{2L}{n\pi}$, $n=1,2,3,\cdots$ coincides with twice the angular frequency. $\{c_n\}$ is called the frequency spectrum or the amplitude spectrum.

d’Alembert (1717-83) studied a partial differential equation (wave equation) that describes motion of a vibrating string and Jacob Bernoulli (1654-1705) showed that its solution is represented as a trigonometric series. Fourier (1768-1830) also showed that the solution of a heat conduction problem is represented as a trigonometric series. Suppose that $f(\theta)$ satisfies $f(\theta+2\pi)=f(\theta)$ for all $\theta$. That is, $f(\theta)$ is a periodic function with period $2\pi$. Assume that $f$ is Riemann integrable on every bounded interval. Then can $f$ be expended in a series (a trigonometric series)
\begin{equation}
\label{eq:fourier}
f(\theta)=\frac{1}{2}a_0+\sum_{n=1}^\infty(a_n\cos n\theta+b_n\sin n\theta)
\end{equation}
? The answer is yes. The series \eqref{eq:fourier} can be written as
\begin{equation}
\label{eq:fourier2}
f(\theta)=\sum_{n=-\infty}^\infty c_ne^{in\theta},
\end{equation}
when $c_0=\frac{1}{2}a_0$, $c_n=\frac{1}{2}(a_n-ib_n)$, and $c_{-n}=\frac{1}{2}(a_n+ib_n)$ for $n=1,2,3,\cdots$.
\begin{align*}
\int_{-\pi}^{\pi}f(\theta)e^{-ik\theta}d\theta&=\sum_{n=-\infty}^\infty c_n\int_{-\pi}^{\pi}e^{i(n-k)\theta}d\theta\\
&=2\pi\sum_{n=-\infty}^\infty c_n\delta_{nk},
\end{align*}
where $\delta_{nk}$ denotes Kronecker’s delta. Hence we obtain
\begin{equation}
\label{eq:fc}
c_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(\theta)e^{-in\theta}d\theta,
\end{equation}
$n=1,2,3,\dots$. $a_n$ and $b_n$ are then given by
\begin{align}
\label{eq:fc2}
a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(\theta)\cos n\theta d\theta,\ n=0,1,2,\cdots,\\
\label{eq:fc3}
b_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(\theta)\sin n\theta d\theta,\ n=1,2,\cdots.
\end{align}
The series of the form \eqref{eq:fourier} or \eqref{eq:fourier2} is called a Fourier series and $c_n$ or $a_n$, $b_n$ are called the Fourier coefficients of $f$.

Lemma. If $F$ is periodic with period $P$ then $\int_a^{a+P} F(x)dx$ is independent of $a$.

Proof. Define
\begin{align*}
g(a)&:=\int_a^{a+P} F(x)dx\\
&=\int_0^{a+P}F(x)dx-\int_0^a F(x)dx.
\end{align*}
Then $g'(a)=F(a+P)-F(a)=0$ for all $a$. This means that $g$ is a constant function.

Lemma. Suppose that $f$ is periodic with period $2\pi$ and integrable on $[-\pi,\pi]$. If $f$ is even,
$$a_n=\frac{2}{\pi}\int_0^\pi f(\theta)\cos n\theta d\theta,\ b_n=0.$$
If $f$ is odd,
$$a_n=0,\ b_n=\frac{2}{\pi}\int_0^\pi f(\theta)\sin n\theta d\theta.$$

Remark. $c_0=\frac{1}{2}a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(\theta)d\theta$. Notice that this is the mean value of $f$ on $[-\pi,\pi]$.

If $f(x)$ is a periodic function with period $2L$, then it can be represented on $[-L,L]$ as
\begin{equation}
\label{eq:fourier3}
f(x)=\frac{1}{2}a_0+\sum_{n=1}^\infty\left\{a_n\cos\left(\frac{n\pi}{L}x\right)+b_n\sin\left(\frac{n\pi}{L}x\right)\right\},
\end{equation}
\begin{align}
\label{eq:fc4}
a_n&=\frac{1}{L}\int_{-L}^L f(x)\cos\left(\frac{n\pi}{L}x\right)dx,\ n=0,1,2,\cdots,\\
\label{eq:fc5}
b_n&=\frac{1}{L}\int_{-L}^L f(x)\sin\left(\frac{n\pi}{L}x\right)dx,\ n=1,2,\cdots.
\end{align}

Example. [Sawtooth Function] Let $f$ be defined by
$$f(x)=x,\ -L<x<L$$
and $f(x+2L)=f(x)$.

Since $x$ is an odd function,
$$a_n=\frac{1}{L}\int_{-}^L x\cos\left(\frac{n\pi}{L}x\right)dx=0,\ n=0,1,2,\cdots.$$
For $n=1,2,\cdots$,
\begin{align*}
b_n&=\frac{1}{L}\int_{-L}^L x\sin\left(\frac{n\pi}{L}x\right)dx\\
&=\frac{2}{L}\int_0^L x\sin\left(\frac{n\pi}{L}x\right)dx\\
&=-\frac{2L(-1)^n}{n\pi}.
\end{align*}
Hence, $f(x)$ is represented as the Fourier series
$$f(x)=-\frac{2L}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{n}\sin\left(\frac{n\pi}{L}x\right)$$
on the interval $[-L,L]$.

Example. [Square Wave] Let $f$ be defined by
$$f(x)=\left\{\begin{array}{ccc}
-k & \mbox{if} & -\pi<x<0\\
k & \mbox{if} & 0<x<\pi
\end{array}\right.$$
and $f(x+2\pi)=f(x)$.

The Fourier coefficients are computed to be
\begin{align*}
a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx=0,\ n=0,1,2,\cdots,\\
b_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\\
&=\frac{2k}{n\pi}[1-(-1)^n],\ n=1,2,\cdots.
\end{align*}
So, $b_n=0$ if $n$ is even. Now,
$$b_{2n-1}=\frac{4k}{(2n-1)\pi},\ n=1,2,\cdots$$
and
$$f(x)=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{\sin(2n-1)x}{2n-1}.$$

Since $0<\frac{\pi}{2}<\pi$, $f\left(\frac{\pi}{2}\right)=k$. On the other hand,
\begin{align*}
f\left(\frac{\pi}{2}\right)&=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{\sin\left(\frac{2n-1}{2}\right)\pi}{2n-1}\\
&=\frac{4k}{\pi}\sum_{n=1}^\infty\frac{(-1)^{n+1}}{2n-1}\\
&=\frac{4k}{\pi}\left(1-\frac{1}{2}+\frac{1}{5}-\frac{1}{7}+\cdots\right).
\end{align*}
Hence, we obtain
$$\frac{\pi}{4}=1-\frac{1}{2}+\frac{1}{5}-\frac{1}{7}+\cdots$$
i.e.
$$\pi=4\sum_{n=1}^\infty\frac{(-1)^{n+1}}{2n-1}.$$
This is a famous result obtained by Gottfried Wilhelm Leibniz in 1673 from geometric considerations.

Gibbs Phenomenon

The Gibbs Phenomenon is an overshoot, a peculiarity of the Fourier series and other eigenfunction series at a simple discontinuity: the $n$th partial sum of the Fourier series has large oscillations near the jump, which may increase the maximum of the partial sum above that of the function itself. The Gibbs phenomenon is observed in the above two examples. The overshoot does not die out as the frequency increases, but approaches to a finite limit. It is a consequence of trying to approximate a discontinuous function with a finite Fourier series i.e. a partial sum of continuous functions which is always continuous.