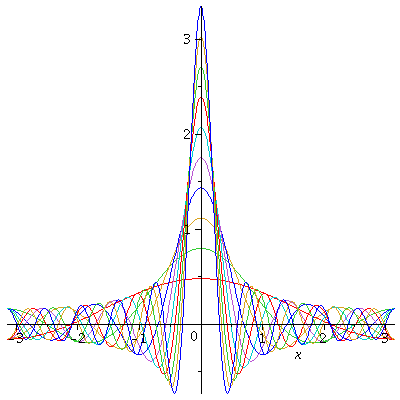In here, we have seen that if a function $f$ is Riemann integrable on every bounded interval, it can be expended as a trigonometric series called a Fourier series by assuming that the series converges to $f$. So, it would be natural to pause the following question. If $f$ is a periodic function, would its Fourier series always converge to $f$? The answer is affirmative if $f$ is in addition piecewise smooth.

Let $S_N^f(\theta)$ denote the $n$-the partial sum of the Fourier series of a $2\pi$-periodic function $f(\theta)$. Then
\begin{equation}
\label{eq:partsum}
\begin{aligned}
S_N^f(\theta)&=\sum_{-N}^N c_ne^{in\theta}\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\psi)e^{in(\theta-\psi)}d\psi\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\psi)e^{in(\psi-\theta)}d\psi.
\end{aligned}
\end{equation}
Let $\phi=\psi-\theta$. Then
\begin{align*}
S_N^f(\theta)&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi+\theta}^{\pi+\theta} f(\phi+\theta)e^{in\phi}d\phi\\
&=\frac{1}{2\pi}\sum_{-N}^N\int_{-\pi}^\pi f(\phi+\theta)e^{in\phi}d\phi\\
&=\int_{-\pi}^\pi f(\theta+\phi)D_N(\phi)d\phi,
\end{align*}
where
\begin{equation}
\label{eq:dkernel}
\begin{aligned}
D_N(\phi)&=\frac{1}{2\pi}\sum_{-N}^N e^{in\phi}\\
&=\frac{1}{2\pi}\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}\\
&=\frac{1}{2\pi}\frac{\sin\left(N+\frac{1}{2}\right)\phi}{\sin\frac{1}{2}\phi}.
\end{aligned}
\end{equation}
$D_N(\phi)$ is called the $N$-th Dirichlet kernel. Note that the Dirichlet kernel can be used to realize the Dirac delta function $\delta(x)$, i.e.
$$\delta(x)=\lim_{n\to\infty}\frac{1}{2\pi}\frac{\sin\left(n+\frac{1}{2}\right)x}{\sin\frac{1}{2}x}.$$

Dirichlet kernel D_n(x), n=1..10, x=-pi..pi

Note that
$$\frac{1}{2}+\frac{\sin\left(N+\frac{1}{2}\right)\theta}{2\sin\frac{1}{2}\theta}=1+\sum_{n=1}^N\cos n\theta\ (0<\theta<2\pi)$$
Using this identity, one can easily show that:

Lemma. For any $N$,
$$\int_{-\pi}^0 D_N(\theta)d\theta=\int_0^{\pi}D_N(\theta)d\theta=\frac{1}{2}.$$

Now, we area ready to prove the following convergence theorem.

Theorem. If $f$ is $2\pi$-periodic and piecewise smooth on $\mathbb{R}$, then
$$\lim_{N\to\infty} S_N^f(\theta)=\frac{1}{2}[f(\theta-)+f(\theta+)]$$
for every $\theta$. Here, $f(\theta-)=\lim_{\stackrel{h\to 0}{h>0}}f(\theta-h)$ and $f(\theta+)=\lim_{\stackrel{h\to 0}{h>0}}f(\theta+h)$. In particular, $\lim_{N\to\infty}S_N^f(\theta)=f(\theta)$ for every $\theta$ at which $f$ is continuous.

Proof. By Lemma,
$$\frac{1}{2}f(\theta-)=f(\theta-)\int_{-\pi}^0 D_N(\phi)d\phi,\ \frac{1}{2}f(\theta+)=f(\theta+)\int_0^\pi D_N(\phi)d\phi.$$
So,
\begin{align*}
S_N^f(\theta)-\frac{1}{2}[f(\theta-)+f(\theta+)]&=\int_{-\pi}^0[f(\theta+\phi)-f(\theta-)]D_N(\phi)d\phi+\\
&\int_0^\pi[f(\theta+\phi)-f(\theta+)]D_N(\phi)d\phi\\
&=\frac{1}{2\pi}\int_{-\pi}^0[f(\theta+\phi)-f(\theta-)]\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}d\phi\\
&+\frac{1}{2\pi}\int_0^\pi[f(\theta+\phi)-f(\theta+)]\frac{e^{i(N+1)\phi}-e^{-iN\phi}}{e^{i\phi}-1}d\phi.
\end{align*}
$$\lim_{\phi\to 0+}\frac{f(\theta+\phi)-f(\theta+)}{e^{i\phi}-1}=\frac{f'(\theta+)}{i},\ \lim_{\phi\to 0-}\frac{f(\theta+\phi)-f(\theta-)}{e^{i\phi}-1}=\frac{f'(\theta-)}{i}.$$
Hence, the function
$$g(\phi):=\left\{\begin{aligned}
&\frac{f(\theta+\phi)-f(\theta+)}{e^{i\phi}-1},\ -\pi<\phi<0,\\
&\frac{f(\theta+\phi)-f(\theta-)}{e^{i\phi}-1},\ 0<\phi<\pi
\end{aligned}\right.$$
is piecewise continuous on $[-\pi,\pi]$. By the corollary to Bessel’s inequality,
$$c_n=\frac{1}{2\pi}\int_{-\pi}^\pi g(\phi)e^{in\phi}d\phi\to 0$$
as $n\to\pm\infty$. Therefore,
\begin{align*}
S_N^f(\theta)-\frac{1}{2}[f(\theta-)+f(\theta+)]&=\frac{1}{2\pi}\int_{-\pi}^\pi g(\phi)[e^{i(N+1)\phi}-e^{-iN\phi}]d\phi\\
&=c_{-(N+1)}-c_N\\
&\to 0
\end{align*}
as $N\to\infty$. This completes the proof.

Corollary. If $f$ and $g$ are $2\pi$-periodic and piecewise smooth, and $f$ and $g$ have the same Fourier coefficients, then $f=g$.

Proof. If $f$ and $g$ have the same Fourier coefficients, their their Fourier series are the same. Due to the conditions on $f$ and $g$, the Fourier series of $f$ and $g$ converge to $f$ and $g$ respectively by the above convergence theorem. Hence, $f=g$.