Theorem (Cauchy-Maclaurin Integral Test)

Let $f(x)$ be a continuous, positive, decreasing function on $[1,\infty)$ in which $f(n)=a_n$. Then $\sum_{n=1}^\infty a_n$ converges if $\int_1^\infty f(x)dx$ is finite and diverges if the integral is infinite.

Proof. Using the left-end point method as seen in Figure 1

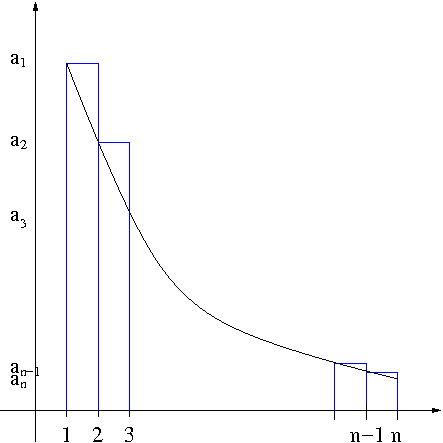
Figure 1. Integral Test

we see that $$a_1+a_2+\cdots+a_{n-1}\geq \int_1^nf(x)dx$$ This means that if $\int_1^{\infty}f(x)dx$ is infinite, $\sum_{n=1}^\infty a_n$ diverges. Now using the right-end point method as seen in Figure 2

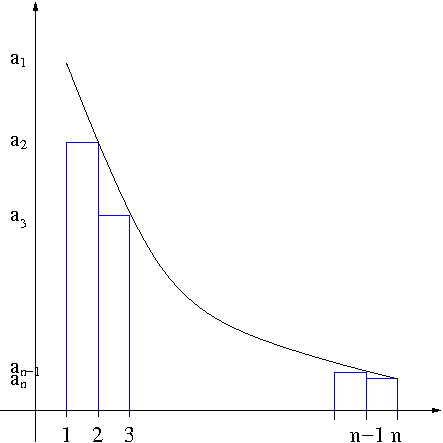
Figure 2. Integral Test

we see that $$a_2+a_3+\cdots+a_n\leq\int_1^n f(x)dx$$ This means that if $\int_1^\infty f(x)dx$ is finite, then $\sum_{n=1}^\infty a_n$ converges. This completes the proof.

Example (The $p$-series).
For what values of $p$ is the series $\sum_{n=1}^\infty\frac{1}{n^p}$ convergent?

Solution. If $p<0$ then $\lim_{n\to\infty}\frac{1}{n^p}=\infty$. If $p=0$ then $\lim_{n\to\infty}\frac{1}{n^p}=1$. In either case, $\lim_{n\to\infty}\frac{1}{n^p}\ne 0$, so the series diverges. If $p>0$ then the function $f(x)=\frac{1}{x^p}$ is continuous, positive and decreasing on $[1,\infty)$.
Now,
$$\int_1^\infty\frac{1}{x^p}dx=\left\{\begin{array}{ccc} \left.\frac{x^{-p+1}}{-p+1}\right|_1^\infty & {\rm if} & p\ne 1,\\ \\ \ln x|_1^\infty & {\rm if} & p=1. \end{array}\right.$$
Therefore the series converges if $p>1$ and diverges if $p\leq 1$.

Example. Test the series $\sum_{n=1}^\infty\frac{1}{n^2+1}$ for convergence or divergence.

Solution. $f(x)=\frac{1}{x^2+1}$ is continuous, positive and decreasing on $[1,\infty)$. $$\begin{align*}\int_1^\infty\frac{1}{x^2+1}dx&=\left.\arctan x\right|_1^\infty\\&=\arctan \infty-\arctan 1\\&=\frac{\pi}{4}\end{align*}$$ Therefore, by the Integral Test the series converges.

Example. Determine whether $\sum_{n=1}^\infty\frac{\ln n}{n}$ converges or diverges.

Solution. $f(x)=\frac{\ln x}{x}$ is continuous, positive and decreasing on $[3,\infty)$. (One can easily check $f(x)$ is decreasing on $(e,\infty)$ by its derivative $f'(x)$.) $$\begin{align*}\int_3^\infty\frac{\ln x}{x}dx&=\frac{1}{2}\left.(\ln x)^2\right|_3^\infty\\&=\infty\end{align*}$$ Therefore, $\sum_{n=1}^\infty \frac{\ln n}{n}$ diverges.

Example. Use the integral test to show that the series $$\sum_{n=1}^\infty\frac{1}{a^{\ln x}}$$ converges if $a>e$ and diverges if $0<a\leq e$.

Proof. Let $f(x)=\frac{1}{a^{\ln x}}$. Then $f(x)$ is positive and continuous on $(1,\infty)$. If $0<a<1$ then the series $\sum_{n=1}^\infty\frac{1}{a^{\ln n}}$ diverges because the sequence $\left\{\frac{1}{a^{\ln n}}\right\}$ is increasing. If $a=e$, the series becomes the harmonic series $\sum_{n=1}^\infty\frac{1}{n}$ which diverges. Now we assume that $1\leq a< e$ or $a>e$. Then $f(x)$ is decreasing $(1,\infty)$. $$\begin{align*}\int_1^\infty\frac{dx}{a^{\ln x}}&=\int_1^\infty a^{-\ln x}dx\\&=-\int_0^{-\infty}a^ue^{-u}du\ (u=-\ln x,\ dx=-xdu=-e^{-u}dx)\\&=\int_{-\infty}^0a^ue^{-u}du\end{align*}$$ Let $v=a^u$ and $dw=e^{-u}du$. Then $dv=a^u\ln a du$ and $w=-e^{-u}$. The integration by parts formula $\int vdw=vw-\int wdv$ results in $$\int a^ue^{-u}du=-a^ue^{-u}+\ln a\int e^{-u}a^udu+C’$$ Hence we find $$\int a^ue^{-u}du=\frac{a^ue^{-u}}{\ln a-1}+C$$ $$\begin{align*}\int_1^\infty\frac{dx}{a^{\ln x}}&=\int_{-\infty}^0a^ue^{-u}du\\&=\left[\frac{a^ue^{-u}}{\ln a-1}\right]_{-\infty}^0\\&=\frac{1}{\ln a-1}\left\{1-\lim_{u\to -\infty}\frac{a^u}{e^u}\right\}\end{align*}$$ While $\frac{a^u}{e^u}$ is an indeterminate form of type $\frac{\infty}{\infty}$, the L’Hôpital’s Rule is not helpful for finding the limit $\lim_{u\to -\infty}\frac{a^u}{e^u}$ as $\frac{(a^u)’}{(e^u)’}=\frac{a^u\ln a}{e^u}$. Instead let $y=\frac{a^u}{e^u}$. Then $\ln y=u(\ln a-1)$. $$\lim_{u\to -\infty}\ln y=\left\{\begin{array}{ccc}-\infty & \mbox{if} & a>e\\\infty & \mbox{if} & a<e\end{array}\right.$$ i.e. $$\lim_{u\to -\infty}\frac{a^u}{e^u}=\left\{\begin{array}{ccc}e^{-\infty}=0 & \mbox{if} & a>e\\e^{\infty}=\infty & \mbox{if} & a<e\end{array}\right.$$ Therefore, $$\int_1^\infty\frac{dx}{a^{\ln x}}=\left\{\begin{array}{ccc}\frac{1}{\ln a-1}<\infty & \mbox{if} & a>e\\\infty & \mbox{if} & a<e\end{array}\right.$$ This completes the proof.

Theorem (Remainder Estimate for the Integral Test)
If $\sum_{n=1}^\infty a_n$ converges by the Integral Test and $R_n=S-s_n$, then
$$\begin{equation}\label{eq:remest}\int_{n+1}^\infty f(x)dx\leq R_n\leq\int_n^\infty f(x)dx\end{equation}$$

Proof. Using the left-end point method we obtain $$R_n=a_{n+1}+a_{n+2}+\cdots\geq\int_{n+1}^\infty f(x)dx$$ as seen in Figure 3.

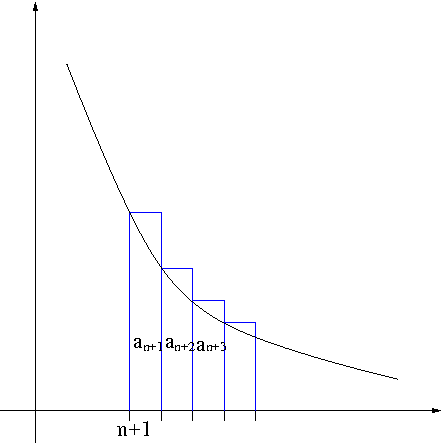
Figure 3. Remainder Estimate

Now using the right-end point method we obtain $$R_n=a_{n+1}+a_{n+2}+\cdots\leq\int_n^\infty f(x)dx$$ as seen in Figure 4.

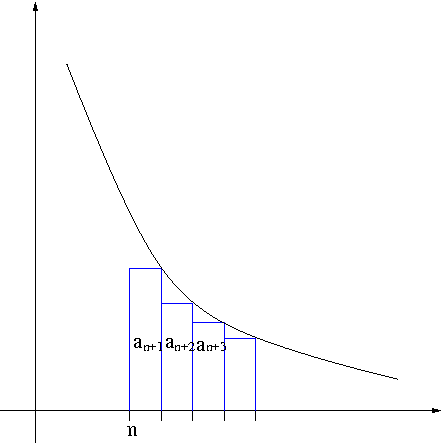
Figure 4. Remainder Estimate

Hence proves $\eqref{eq:remest}$.

Example.

1. Approximate the sum of the series $\sum_{n=1}^\infty\frac{1}{n^3}$ by using the sum of the first 10 terms. Estimate the error involved in this approximation.
2. How many terms are required to ensure that the sum is accurate to within $0.0005$?

Solution. First we calculate $$\int_n^\infty\frac{1}{x^3}dx=\frac{1}{2n^2}$$

1. $s_{10}=\frac{1}{1^3}+\frac{1}{2^3}+\cdots+\frac{1}{10^3}\approx 1.197532$. By the remainder estimate $\eqref{eq:remest}$ $$R_{10}\leq\int_{10}^\infty\frac{1}{x^3}dx=\frac{1}{200}=0.005$$ So the size of the error is at most 0.005.
2. $R_n\leq\int_n^\infty\frac{1}{x^3}dx=\frac{1}{2n^2}$.  Suppose $\frac{1}{2n^2}<0.0005$. Then we find $n>\sqrt{1000}\approx 31.6$. This means we need 32 terms to guarantee accuracy to within 0.0005.

Corollary. $$\begin{equation}\label{eq:sumest}s_n+\int_{n+1}^\infty f(x)dx\leq s\leq s_n+\int_n^\infty f(x)dx\end{equation}$$

Proof. Add $s_n$ to each side of the inequalities in $\eqref{eq:remest}$

Example. Use the inequality $\eqref{eq:sumest}$ with $n=10$ to estimate the sum of the series $\sum_{n=1}^\infty\frac{1}{n^3}$.

Solution. Using $\eqref{eq:sumest}$ for $n=10$ we have $$s_{10}+\int_{11}^\infty\frac{1}{x^3}dx\leq s\leq s_{10}+\int_{10}^\infty\frac{1}{x^3}dx$$ i.e. $$s_{10}+\frac{1}{2(11)^2}\leq s\leq s_{10}+\frac{1}{2(10)^2}$$ Hence we get $$1.201664\leq s\leq 1.202532$$ We can approximate $s$ by taking the midpoint of this interval (i.e. the average of the boundary points) which is $s\approx 1.2021$. The error is then at most half the length of the interval i.e. the error is smaller than 0.0005. Recall that we had to use 32 terms to make error smaller than 0.0005 in the previous example but in this example we needed only 10 terms. So we can obtain a much improved estimate using $\eqref{eq:sumest}$ than using $s_n$.

Definition. Let $a_1,a_2,\cdots,a_n\cdots$ be any sequence of quantities. Then the symbol
$$\begin{equation} \label{eq:series} \sum_{n=1}^\infty a_n=a_1+a_2+\cdots+a_n+\cdots \end{equation}$$
is called an infinite series. Let
$$\begin{align*} s_1&=a_1,\\ s_2&=a_1+a_2,\\ s_3&=a_1+a_2+a_3,\\ \cdots\\ s_n&=a_1+a_2+a_3+\cdots+a_n,\\ \cdots \end{align*}$$
The numbers $s_n$ is called the $n$-th partial sums of the series $\eqref{eq:series}$.

Definition. An infinite series $\sum_{n=1}^\infty a_n$ is said to converge if the sequence of partial sums $\{s_n\}$ converges i.e. $\sum_{n=1}^\infty a_n=s<\infty$ means that for any $\epsilon>0$ there exists a positive integer $N$ such that
$$|s_n-s|<\epsilon\ \mbox{for all}\ n\geq N$$ A series which does not converge is said to diverge.

Remark. It should be noted that there is no unique way to define the sum of an infinite series. While the definition we use is the conventional one, there are other ways to define the sum of an infinite series. Some of the divergent series according to the conventional definition may converge with a different definition. Although it may seem outrageous it can be shown that $1+2+3+\cdots=-\frac{1}{12}$. It was first proved by the genius Indian mathematician Srinivasa Ramanujan. If you have a Netflix account, you can watch a biographical movie about Ramanujan. The movie title is The Man Who Knew Infinity which is based on a biography by Robert Kanigel The Man Who Knew Infinity: A Life of the Genius Ramanujan. I find divergent series fascinating. In case you are interested, I wrote about divergent series in blog articles here and here.

Proposition. If $\sum_{n=1}^\infty a_n$ converges, then $\lim_{n\to\infty}a_n=0.$

Note that the converse of the proposition is not necessarily true. See the example on harmonic series below. The proposition, more precisely its contrapositive

If $\lim_{n\to\infty}a_n\ne 0$, then $\sum_{n=1}^\infty a_n$ diverges.

can be used as a divergence test for series. For example, the series $\sum_{n=1}^\infty\frac{n}{n+1}$ diverges because $\lim_{n\to\infty}\frac{n}{n+1}=1\ne 0$.

Theorem (Cauchy’s Criterion for the Convergence of a Sequence).
A necessary and sufficient condition for the convergence of a sequence $\{a_n\}$ is that for any $\epsilon>0$ there exists a positive integer $N$ such that
$$|a_n-a_m|<\epsilon\ \mbox{for all}\ n,m\geq N.$$

Corollary (Cauchy’s Criterion for the Convergence of a Series).
A necessary and sufficient condition for the convergence of a series $\sum_{n=1}^\infty u_n$ is that for any $\epsilon>0$ there exists a positive integer $N$ such that
$$|s_n-s_m|<\epsilon\ \mbox{for all}\ n,m\geq N.$$

Example (The Geometric Series).
The geometric sequence, starting with $a$ and ratio $r$, is given by
$$a, ar,ar^2,\cdots,ar^{n-1},\cdots.$$
The $n$th partial sum is given by
$$s_n=a\frac{1-r^n}{1-r}.$$
Taking the limit as $n\to\infty$,
$$\lim_{n\to\infty}s_n=\frac{a}{1-r}\ \mbox{for}\ -1<r<1.$$
Hence the infinite geometric series converges for $-1<r<1$ and is given by
$$\sum_{n=1}^\infty ar^{n-1}=\frac{a}{1-r}.$$
On the other hand, if $r\leq -1$ or $r\geq 1$ then the infinite series diverges. For example, the series $$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots$$ is a geometric series with $a=\frac{1}{2}$ and $r=\frac{1}{2}$. Since $-1<r<1$, the series $\sum_{n=1}^\infty\left(\frac{1}{2}\right)^n$ converges to $\frac{\frac{1}{2}}{1-\frac{1}{2}}=\frac{1}{2}$.

Geometric series also can be used to write repeating decimal expansions to fractions. For example, let us write $1.0\overline{35}$ as a fraction. $$\begin{align*}1.0\overline{35}&=1.035353535\cdots\\&=1+0.035+0.00035+0.0000035+\cdots\\&=1+\frac{35}{10^3}+\frac{35}{10^5}+\frac{35}{10^7}+\cdots\\&=1+\frac{35}{10^3}\left(1+\frac{1}{10^2}+\frac{1}{10^4}+\cdots\right)\\&=1+\frac{35}{10^3}\frac{1}{1-\frac{1}{10^2}}\\&=1+\frac{35}{990}=\frac{1025}{990}=\frac{205}{198}\end{align*}$$ In practice, there is an easier and a quicker way to convert a repeating decimal expansion to a fraction as you may have learned in high school or earlier: $$1000\times 1.0\overline{35}-10\times  1.0\overline{35}=1035-10=1025$$ so $$1.0\overline{35}=\frac{1025}{990}=\frac{205}{198}$$

Example (The Harmonic Series).
Consider the harmonic series
$$\sum_{n=1}^\infty\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\cdots.$$
Group the terms as
$$1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right) +\left(\frac{1}{9}+\cdots+\frac{1}{16}\right)+\cdots.$$
Then each pair of parentheses encloses $p$ terms of the form
$$\frac{1}{p+1}+\frac{1}{p+2}+\cdots+\frac{1}{p+p}>\frac{p}{2p}=\frac{1}{2}.$$
Forming partial sums by adding the parenthetical groups one by one, we obtain
$$s_1=1, s_2=1+\frac{1}{2}, s_4>1+\frac{2}{2}, s_8>1+\frac{3}{2}, s_{16}>1+\frac{4}{2},\cdots, s_{2^n}>1+\frac{n}{2},\cdots.$$
This shows that $\lim_{n\to\infty}s_{2^n}=\infty$ and so $\{s_n\}$ diverges. Therefore, the harmonic series diverges.

Example. The following type of series are called telescoping series. #2 is left as an exercise.

1. Show that
   $$\sum_{n=1}^\infty\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}$$ Solution. $$\begin{align*}s_n&=\sum_{k=1}^n\frac{1}{(2k-1)(2k+1)}\\&=\frac{1}{2}\sum_{k=1}^n\left(\frac{1}{2k-1}-\frac{1}{2k+1}\right)\\&=\frac{1}{2}\left(1-\frac{1}{2n+1}\right)\\&=\frac{n}{2n+1}\end{align*}$$ and $\lim_{n\to\infty}s_n=\frac{1}{2}$.
2. Show that $$\sum_{n=1}^\infty\frac{1}{n(n+1)}=1$$

Definition. A succession of real numbers $$a_1,a_2,\cdots,a_n,\cdots$$ in a definite order is called a sequence. $a_n$ is called the $n$-th term or the general term. The sequence $\{a_1,a_2,\dots,a_n,\cdots\}$ is denoted by $\{a_n\}$ or $\{a_n\}_{n=1}^\infty$.

Example.

1. The set of natural numbers $1,2,3,4,\cdots,n,\cdots$
2. $1,-2,3,-4,\cdots,(-1)^{n-1}n,\cdots$
3. $\frac{1}{2},-\frac{1}{4},\frac{1}{8},-\frac{1}{16},\cdots,(-1)^{n-1}\frac{1}{2^n},\cdots$
4. $0,1,0,1,\cdots,\frac{1}{2}[1+(-1)^n],\cdots$
5. $2,3,5,7,11,\cdots,p_n,\cdots$

It is not essential that the general term of a sequence is given by some simple formula as is the case in the first four examples above. The sequence in 5 represents the succession of prime numbers. $p_n$ stands for the $n$-th prime number. There is no formula available for the determination of $p_n$.

The following is the quantifying definition of the limit of a sequence due to Augustin-Louis Cauchy.

Definition. A sequence $\{a_n\}$ has a limit $L$ and we write $\lim_{n\to\infty}a_n=L$ or $a_n\to L$ as $n\to\infty$ if for any $\epsilon>0$ there exists a positive integer $N$ such that $$|a_n-L|<\epsilon\ \mbox{for all}\ n\geq N.$$

Example.

1. Show that $\lim_{n\to\infty}\frac{1}{n}=0$
2. Show that $\lim_{n\to\infty}\frac{1}{10^n}=0$
3. Let $\{a_n\}$ be a sequence defined by $$a_1=0.3, a_2=0.33, a_3=0.333,\cdots,$$ show that $\lim_{n\to\infty}a_n=\frac{1}{3}$

Proof. I will prove 1. 2 and 3 are left as exercises. Let $\epsilon>o$ be given. Then $|a_n-L|=\frac{1}{n}<\epsilon\Longrightarrow n>\frac{1}{\epsilon}$. Choose $N$ a positive integer $\frac{1}{\epsilon}$. Then for all $n>N$ $|a_n-L|<\epsilon$.

The following limit laws allow us to break a complicated limit to simpler ones.

Theorem. Let $\lim_{n\to\infty}a_n=L$ and $\lim_{n\to\infty}b_n=M$. Then

1. $\lim_{n\to\infty}(a_n\pm b_m)=L\pm M$
2. $\lim_{n\to\infty}ca_n=cL$ where $c$ is a constant.
3. $\lim_{n\to\infty}a_nb_n=LM$
4. $\lim_{n\to\infty}\frac{a_n}{b_n}=\frac{L}{M}$ provided $M\ne 0$.

Example. Find $\lim_{n\to\infty}\frac{n}{n+1}$.

Solution. $$\begin{align*}\lim_{n\to\infty}\frac{n}{n+1}&=\lim_{n\to\infty}\frac{1}{1+\frac{1}{n}}=1\end{align*}$$ since $\lim_{n\to\infty}\frac{1}{n}=0$.

The following theorem is also an important tool for calculating limits of certain sequences.

Theorem (Squeeze Theorem). If $a_n\leq b_n\leq c_n$ for $n\geq n_0$ and $\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=L$ then $\lim_{n\to\infty}b_n=L$.

Corollary. If $\lim_{n\to\infty}|a_n|=0$ then $\lim_{n\to\infty}a_n=0$.

Proof. It follows from the inequality $-|a_n|\leq a_n\leq |a_n|$ for all $n$ and the Squeeze Theorem.

Example. Use the Squeeze Theorem to show $$\lim_{n\to\infty}\frac{n!}{n^n}=0$$

Solution. It follows from $$0\leq\frac{n!}{n^n}=\frac{1\cdot 2\cdot 3\cdots n}{n\cdot n\cdot n\cdots n}\leq\frac{1}{n}$$ for all $n$.

The following theorem enables you to use a cool formula you learned in Calculus I, L’Hôpital’s rule!

Theorem. If $\lim_{x\to\infty}f(x)=L$ and $f(n)=a_n$, then $\lim_{n\to\infty}a_n=L$.

Example. Calculate $\lim_{n\to\infty}\frac{\ln n}{n}$.

Solution. Let $f(x)=\frac{\ln x}{x}$. Then $\lim_{x\to\infty}f(x)$ is an indeterminate form of  type $\frac{\infty}{\infty}$. So by L’Hôpital’s rule $$\begin{align*}\lim_{x\to\infty}\frac{\ln x}{x}&=\lim_{x\to\infty}\frac{(\ln x)’}{x’}\\&=\lim_{x\to\infty}\frac{1}{x}\\&=0\end{align*}$$ Hence by the Theorem above $\lim_{n\to\infty}\frac{\ln n}{n}=0$.

Example. Calculate $\lim_{n\to\infty}\root n\of{n}$.

Solution. Let $f(x)=x^{\frac{1}{x}}$. Then $\lim_{x\to\infty}f(x)$ is an indeterminate form of type $\infty^0$. As you learned in Calculus I, you will have to convert the limit into an indeterminate form of type $\frac{\infty}{\infty}$ or type $\frac{0}{0}$ so that you can apply L’Hôpital’s rule to evaluate the limit. Let $y=x^{\frac{1}{x}}$. Then $\ln y=\frac{\ln x}{x}$. As we calculated in the previous example, $\lim_{x\to\infty}\ln y=0$. Since $\ln y$ is continuous on $(0,\infty)$, $$\lim_{x\to\infty}\ln y=\ln(\lim_{x\to\infty} y)$$ Hence, $$\lim_{x\to\infty}x^{\frac{1}{x}}=e^0=1$$ i.e. $\lim_{n\to\infty}\root n\of{n}=1$.

Theorem. $\lim_{n\to\infty}\root n\of{a}=1$ for $a>0$.

Example. $\lim_{n\to\infty}\frac{1}{\root n\of{2}}=1$.

Definition. A sequence $\{a_n\}$ is said to diverge if it fails to converge. Divergent sequences include sequences that tend to infinity or negative infinity, for example $1,2,3,\cdots,n,\cdots$ and sequences that oscillates such as  $1,-1,1,-1,\cdots$.

Definition. A sequence $\{a_n\}$ is said to be bounded if there exists $M>0$ such that $|a_n|<M$ for every $n$.

Theorem. A convergent sequence is bounded but the converse need not be true.

Definition. A sequence $\{a_n\}$ is said to be monotone if it satisfies either $$a_n\leq a_{n+1}\ \mbox{for all}\ n$$ or $$a_n\geq a_{n+1}\ \mbox{for all}\ n$$

Equivalently, one can show that a sequence $\{a_n\}$ is monotone increasing by checking to see if it satisfies   $$\frac{a_{n+1}}{a_n}\geq 1\ \mbox{for all}\ n$$ or $$a_{n+1}-a_n\geq 0\ \mbox{for all}\ n$$

The following theorem is called the Monotone Sequence Theorem.

Theorem. A monotone sequence which is bounded is convergent.

Example.

1. Show that the sequence $$\frac{1}{2},\frac{1}{3}+\frac{1}{4},\frac{1}{4}+\frac{1}{5}+\frac{1}{6},\cdots,\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{2n},\cdots$$ is convergent.
2. Show that the sequence $$1,1+\frac{1}{2},1+\frac{1}{2}+\frac{1}{4},\cdots,1+\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^n},\cdots$$ is convergent.

Solution. 2 is left as an exercise. $a_{n+1}-a_n=\frac{1}{2n+2}+\frac{1}{2n+1}-\frac{1}{n+1}=\frac{4n+1}{(2n+2)(2n+1)}>0$ for all $n$. So it is monotone increasing. $$a_n=\frac{1}{n+1}+\cdots+\frac{1}{n+n}\leq\frac{1}{n}+\cdots+\frac{1}{n}=\frac{n}{n}=1$$ for all $n$. So it is bounded. Therefore, it is convergent by the monotone sequence theorem.