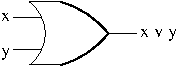
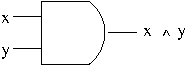
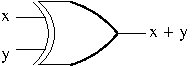
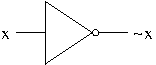
Directed graphs represent binary relations. They can be visualized as diagrams made up of points (called vertices or nodes) and arrows (called arcs or edges). Draw an arc from a vertex $v$ to a vertex $w$ to represent that $v$ is related to $w$ i.e. the ordered pair $(v,w)$ is in the relation.

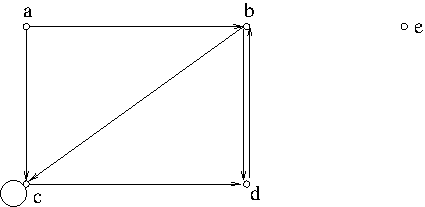
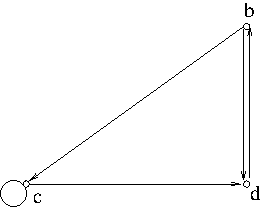
Example 1. An example of a directed graph

Definition. A directed graph or digraph in short is an ordered pair $(V,A)$ where $V$ is an nonempty set and $A\subseteq V\times V$ (i.e. $A$ is a binary relation on $V$). The members of $V$ are called vertices or nodes and the members of $A$ are called arcs or edges. We write arcs as $v\to w$ rather than $(v,w)$.

In Example 1, $V=\{a,b,c,d,e\}$ and \begin{align*}A&=\{(a,b), (b,c), (a,c), (c,c), (c,d), (b,d),(d,b)\}\\&=\{a\to b, b\to c, a\to c, c\to c, c\to d, b\to d, d\to b\}\end{align*}

Transportation and computer networks have natural representations of digraphs.

A walk in a digraph is a way of proceeding through a sequence of vertices by following arcs i.e. a walk in a digraph $(V,A)$ is a sequence of vertices $v_0,v_1,\cdots,v_n\in V$ for some $n\geq 0$ such that $v_i\to v_{i+1}\in A$ for each $i<n$. The length of this walk is $n$ which is the number of arcs.

Example 2. In Example 1, $b\to d$, $b\to c\to d$, $b\to c\to c\to d$, $b\to d\to b\to d$ are examples of walks from vertex $b$ to vertex $d$. The length of $b\to d$ is 1, the length of $b\to c\to d$ is 2, the length of $b\to c\to c\to d$ is 3 and the length of $b\to d\to b\to d$ is also 3. There is no walk from vertex $b$ to vertex $a$.

A path is a walk that doesn’t repeat any vertex.

Example 3. Among the walks in Example 2, $b\to d$ and $b\to c\to d$ are paths from vertex $b$ to $d$.

A walk in which the first and the last vertex are the same is called a circuit. A circuit is called a cycle if the first and the last vertices are the only repeated vertex. For example, $b\to c\to c\to b\to b$ in the digraph in Example 1 is a circuit but is not a cycle. On the other hand, $b\to c\to d\to b$ is a cycle of length 3, $b\to d\to b$ is a cycle of length 2, and $c\to c$ is a cycle of length 1.

A digraph without any cycles is said to be acyclic. The digraph in Exam 1 is not acyclic as it contains cycles.

A walk can be reduced to a path by removing nontrivial cycles. Suppose that a walk from $v$ to $w$ $$v=v_0\to\cdots\to v_n=w$$ includes a cycle $v_i\to v_{i+1}\to\cdots\to v_j$ where $i<j$ and $v_i=v_j$. Then $$v=v_0\to\cdots\to v_i\to v_{j+1}\to\cdots\to v_n=w$$ is a shorter walk from $v$ to $w$.

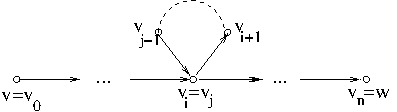
For example, the walk $b\to d\to b\to d$ in Example 1 can be reduced to the path $b\to d$ by removing the cycle $b\to d\to d$.

A vertex $w$ is said to be reachable from vertex $v$ if there is a walk or a path from $v$ to $w$. The distance from vertex $v$ to vertex $w$ in a digraph $G$, denoted by $d_G(v,w)$, is the length of the shortest path from $v$ to $w$, or is defined to be $\infty$ if there is no path from $v$ to $w$. For example, the distance from $a$ to $d$ in the digraph in Example 1 is 2 because the shortest path is $a\to c\to d$.

Lemma. The distance from one vertex of a graph to another vertex is at most the length of any walk from the first to the second.

Proof. It follows from the fact that any walk from $v$ to $w$ includes among its arcs a path from $v$ to $w$.

A digraph in which every vertex is reachable from every other vertex is said to be strongly connected.

Let $G=(V,A)$ be a digraph. Let $V’\subseteq V$ and $A’\subseteq A$. Then $(V’,A’)$ is called a subgraph of $G$. $(V,\emptyset)$ is a subgraph of $G$.

Let $G=(V,A)$ be a digraph and $V’\subset V$. Then $$(V’,\{v\to w\in A: v,w\in V’\})$$ is called the subgraph induced by $V’$.

Example 4. The subgraph induced by $V\setminus\{e\}$ in Example 1 is not strongly connected. But the subgraph induced by $\{b,c,d\}$ is strongly connected.

An acyclic digraph is generally called a directed acyclic group or DAG in short.

The out-degree of a vertex is the number of arcs leaving it i.e. $|\{w\in V: v\to w\ \mbox{in}A\}|$. Similarly, the in-degree of a vertex is the number of arcs entering it.

Theorem. A finite DAG has at least one vertex of out-degree 0 and at least one vertex of in-degree 0.

Proof. Let $G=(V,A)$ be a finite DAG. Suppose that $G$ has no vertex of out-degree 0.

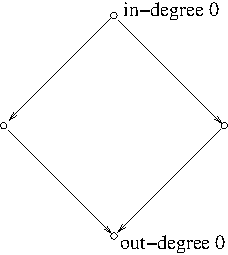
Pick a vertex $v_0$. Since $v_0$ has a positive out-degree, there exists an arc $v_0\to v_1$ for some vertex $v_1$. Since $v_1$ has a positive out-degree, there exists an arc $v_1\to v_2$ for some vertex $v_2$. One can continue doing this. But since $V$ is finite, some vertex will be repeated, creating a cycle. This is a contradiction to the graph $G$ being acyclic. A very similar argument can be made to show that $G$ has a vertex of in-degree 0.

In a DAG, a vertex of in-degree 0 is called a source and a vertex of out-degree 0 is called a sink.

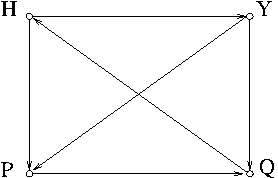
A tournament graph

A tournament graph is a digraph in which every pair of distinct vertices are connected by an arc in one direction or the other, but not both. It is a natural representation of a round-robin tournament in which each players competes with all other plays in turn.

Example 5. The tournament graph in Figure 6 shows that $H$ beats both $P$ and $Y$, $Q$ beats $H$, $Y$ beats $P$, and $P$ beats $Q$. Hence we have a cycle $H\to P\to Q\to H$. Awkwardly, there is no champion!

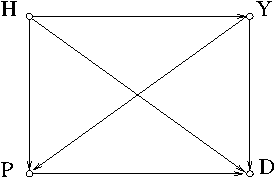
Example 6. The tournament graph in Figure 7 shows that $H$ beats $P$, $Y$, $D$, $Y$ beats $P$ and $D$, and $P$ beats $D$. Hence, $H$ is the first, $Y$ is the second, $P$ the third, and $D$ is the fourth places.

The total number of arcs in a tournament graph with $n$ vertices is $\frac{n(n-1)}{2}$, since there is exactly one arc between each pair of distinct vertices.

A linear order, denoted by $\preceq$, is a binary relation on a finite set $S=\{s_0,s_1,\cdots,s_n\}$ such that $s_i\preceq s_j$ if and only if $i\leq j$.

Example 7. Let $S=\{\mbox{all English words}\}$. Define $s_i\preceq s_j$ to mean that $s_i$ appears before $s_j$ alphabetically or they are equal. Then $\preceq$ is a linear order. This particular linear order is called the lexicographic order or the dictionary order.

A strict order of a finite set, denoted by $\prec$, is an ordering such that $s_i\prec s_j$ if and only if $i<j$.

Theorem. A tournament graph represents a strict linear order if and only if it is a DAG.

Proof. Let $G=(V,A)$ be a tournament graph. Suppose that $G$ represents a strict order. This means that the path $$v_0\to v_1\to\cdots\to v_n$$ represents $$v_0\prec v_1\prec\cdots\prec v_n$$ so every arc goes from $v_i$ to $v_j$ if $i<j$. The graph is then acyclic because any cycle will have to include at least one arc $v_j\to v_i$ where $i<j$. Conversely suppose $G$ is a DAG. We show by induction that $G$ represents a strict order. If $G$ has only one vertex, clearly $G$ represents a strict order. If $G$ has more than one vertex, at least one of the vertices, say $v_0$, has in-degree 0. Since $G$ is a tournament graph, $G$ must contain each of the arc $v_0\to v_i$ ($i\ne 0$). Consider the subgraph induced by $V\setminus\{v_0\}$. This induced subgraph is also a DAG, since all its arcs are arcs of $G$. It is also a tournament graph. The subgraph includes all the arcs of $G$ except those entering from $v_0$. By induction hypothesis, the induced subgraph represents a strict linear order $$v_1\prec v_2\prec\cdots\prec v_n$$ Since $v_0\prec v_i$ for all $i\ne 0$, we have $$v_0\prec v_1\prec\cdots\prec v_n$$ This completes the proof.

Example 8. The tournament graph in Example 7 is a DAG and it represents a strict order $H\prec Y\prec P\prec D$, while the tournament graph in Example 6 doesn’t. (It is not a DAG.)

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019

Quantificational logic is an extension of propositional logic. It is logic of expressions such as “for any”, “for all”, “there is some”, and “there is exactly one”. Quantificational logic is also called first-order logic, predicate logic, or predicate calculus. The universal quantifier $\forall$ means “for all”, “for each”, “for any”, or “for every”. The existential quantifier $\exists$ means “there exists”.

Example. $\forall x\exists y P(x,y)$

Quantificational formulae such as the one in the above example are merely strings of symbols which do not mean anything (i.e. being true or false) as logical statements until they are accompanied by proper interpretations. An interpretation of a quantificational formula has to specify the following.

1. The universe $U$, the nonempty set from which the values of the variables ($x$, $y$, $z$, etc.) are drawn.
2. For each, say $k$-ary, predicate symbol $P$, which $k$-tuples of members of $U$ the predicate is true of, and
3. What elements of the universe correspond to any constant symbols, and what functions from the universe to itself correspond to function symbols mentioned in the formula.

Example. Let $U=\{0,1\}$ and $P$ be the less-than relation i.e. $P(x,y)$ is “$x$ is less than $y$.” Then

• $P(0,0)$ is false
• $P(0,1)$ is true
• $P(1,0)$ is false
• $P(1,1)$ is false

The quantificational formula $\forall x\exists y P(x,y)$ is false because there is no value of $y$ in the universe for which $P(x,y)$ is true when $x=1$.

Example. Let $U=\{0,1\}$ and $P$ be the not-equal relation i.e. $P(x,y)$ is “$x$ is not equal to $y$.” Then

• $P(0,0)$ is false
• $P(0,1)$ is true
• $P(1,0)$ is true
• $P(1,1)$ is false

Hence $\forall x\exists y P(x,y)$ is true.

In general, the universe of an interpretation is an infinite set, so it is impossible to specify the values of the predicate for every combination of elements. For a remedy, we restate the definition in terms of relations by saying an interpretation of a quantificational formula consists of

1. a nonempty set called the universe
2. for each $k$-place predicate symbol, a $k$-ary relation on the universe
3. for each $k$-place function symbol, a $k$-ary function from the universe to itself.

Example. Let $U=\mathbb{N}$, the set of natural numbers and $P$ be the less-than relation. Then the formula $\forall x\exists y P(x,y)$ is true.

Example. Let $U=\mathbb{N}$ and $P$ be the greater-than relation. Then the formula $\forall x\exists y P(x,y)$ is false.

Example. An example of a formula involving a function. Let $U=\mathbb{N}$ and $P(x,y)$ be $\forall x\exists y(x+y=0)$. The constant symbol 0 is interpreted as zero and the binary function symbol $+$ represents addition. The formula is false. For example, when $x=1$, there is no value of $y$ in the universe such that $x+y=0$. If $U=\mathbb{Z}$, the set of integers, however, the formula is true.

Two formulae are equivalent if they are true under the same interpretation.

Example. $\forall x\exists y P(x,y)$ and $\forall y\exists x P(y,x)$ are equivalent.

If two formulae $F$ and $G$ are equivalent, we write $F\equiv G$.

A model of a formula is an interpretation in which it is true. A satisfiable formula of quantificational logic is one that has a model. A valid formula, also called theorem, is a formula that is true under every interpretation. Valid formulae are the quantificational analogs of tautologies in propositional logic.

Example. $\forall x(P(x)\wedge Q(x))\Longrightarrow\forall y P(y)$ is a valid formula. $\forall x P(x)\wedge\exists y\neg P(y)$ is unsatisfiable.

Note. $\exists x (H(x)\wedge B(x))\not\equiv\exists xH(x)\wedge\exists x B(x)$. $\exists x (H(x)\wedge B(x))\not\equiv\exists x H(x)\wedge B(x)$. $x$ in $B(x)$ in the second formula is a free variable i.e. $\exists x H(x)\wedge B(x)\equiv(\exists x H(x))\wedge B(x)$$

The laws we learned in propositional logic are carried over. For example, Distributive Laws \begin{align}\forall x(P(x)\wedge(Q(x)\vee R(x)))&\equiv\forall x((P(x)\wedge Q(x))\vee(P(x)\wedge R(x)))\label{eq:distlaw1}\\\forall x(P(x)\vee(Q(x)\wedge R(x)))&\equiv\forall x((P(x)\vee Q(x))\wedge(P(x)\vee R(x)))\label{eq:distlaw2}\end{align}

Quantificational Equivalence Rule 1 (Proposition Substitutions)

Suppose $F$ and $G$ are quantificational formulae and $F’$ and $G’$ are propositional formulae that result from $F$ and $G$, respectively, by replacing each subformula by a corresponding propositional variable at all of its occurrences in both $F$ and $G$. Suppose $F’\equiv G’$ as formulae of propositional logic. Then replacing $F$ by $G$ in any formula results n an equivalent formula.

Example. $\forall x\neg\neg P(x)\equiv\forall x P(x)$ since $p\equiv\neg\neg p$ and so $\neg\neg P(x)$ can be replaced by $P(x)$.

Example. Replacing $P(x)$, $Q(x)$ and $R(x)$ by $p$, $q$ and $r$, respectively, turns $P(x)\wedge(Q(x)\vee R(x))$ into $p\wedge(q\vee r)$ and $(P(x)\wedge Q(x))\vee(P(x)\wedge R(x))$ into $(p\wedge q)\vee(p\wedge r)$. Since $p\wedge(q\vee r)\equiv (p\wedge q)\vee(p\wedge r)$, $P(x)\wedge(Q(x)\vee R(x))$ can be replaced by $(P(x)\wedge Q(x))\vee(P(x)\wedge R(x))$. Hence we have the equivalence in \eqref{eq:distlaw1}.

Quantificational Equivalence Rule 2 (Change of Variables)

Let $F$ be a formula containing a subformula $\Box x G$, where $\Box$ is either $\forall$ or $\exists$. Assume $G$ has no bound occurrence of $x$ and let $G’$ be the result of replacing $x$ by $y$ everywhere in $G$. Then replacing $\Box x G$ by $\Box y G’$ within the formula results in an equivalent formula.

Example. $\exists x (H(x)\wedge B(x))\equiv\exists y (H(y)\wedge B(y))$

Quantificational Equivalence Rule 3 (Quantifier negation)

\begin{align*}\neg\forall x F&\equiv\exists x\neg F\\\neg\exists x F&\equiv\forall x\neg F\end{align*}

Quantificational Equivalence Rule 4 (Scope change)

Suppose the variable $x$ does not appear in $G$. Let $\Box$ denote either $\forall$ or $\exists$. Let $\diamond$ denote either $\vee$ or $\wedge$. Then \begin{align*}(\Box x F\diamond G)&\equiv\Box x(F\diamond G)\\(G\diamond\Box x F)&\equiv\Box x(G\diamond F)\end{align*}

Example. Let $r$ be “it rains”, $\mathrm{outside(x)}$ “$x$ is outside” and $\mathrm{wet}(x)$ “$x$ gets wet”. Then “If it is raining, then anything that is outside will get wet” is written as the quantificational formula $$r\Longrightarrow\forall x(\mathrm{ouside}(x)\Longrightarrow\mathrm{wet}(x))$$ This is equivalent to $$\forall x(r\Longrightarrow(\mathrm{ouside}(x)\Longrightarrow\mathrm{wet}(x)))$$ as a consequence of scope change. The transformed formula says, in plain English, “Any object, if it is raining, will get wet if it is outside” which sounds less natural than the original statement.

Example. As a consequence of scope change we obtain \begin{align*}(\forall x P(x)\vee\exists y Q(y))&\equiv\forall x\exists y (P(x)\vee Q(x))\\&\equiv\exists y\forall x(P(x)\vee Q(y))\end{align*}

Example. For $(\forall x P(x)\vee\exists x Q(x))$, neither quantifiers can be moved out because the quantified variable $x$ appears in both subformulae. However, instead of scope change one can use change of variable rule to turn it into $(\forall x P(x)\vee\exists y Q(y))$ which is shown in the previous example.

Through repeated application of the quantificational equivalence rules, all quantifiers can be pulled out to the beginning of the formula. Such a formula is said to be in prenex normal form.

Example. Let $L(x,y)$ be “$x$ loves $y$”. Then the statement “everyone has a unique beloved” can be written as the quantificational formula $$\forall x\exists y (L(x,y)\wedge\forall z (L(x,z)\Longrightarrow y=z)$$ It can be transformed to the formula in prenex form $$\forall x\exists y\forall z(L(x,y)\wedge(L(x,z)\Longrightarrow y=z))$$

Example. Translate into quantificational logic and put into prenex form: “If there are any ants, then one of them is the queen.”

Solution. Let $A(x)$ be “$x$ is an ant and $Q(x)$ “$x$ is a queen.” Then the statement can be written as the quantificational formula $$\exists x A(x)\Longrightarrow\exists y (A(y)\wedge Q(y)\wedge\forall z (Q(z)\Longrightarrow z=y))$$ It’s direct translation is “If there exists an $x$ such that $x$ is an ant, then there exists a $y$ such that $y$ is an ant and $y$ is a queen and any $z$ that is a queen is equal to $y$.” The formula can be transformed to \begin{align*}\neg\exists x A(x)\vee\exists y(A(y)\wedge Q(y)\wedge\forall z (Q(z)\Longrightarrow z=y))&\equiv\forall x\neg A(x)\wedge\exists y(A(y)\wedge Q(y)\wedge\forall z (Q(z)\Longrightarrow z=y))\\&\equiv\forall x\exists y\forall z(\neg A(x)\vee(A(y)\wedge Q(y)\wedge\forall z (Q(z)\Longrightarrow z=y))\end{align*}

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019

Computers are built on (propositional) logic. The reason ( ) around “propositional” is that propositional logic is not the only choice of logic for computers. There are ternary computers based on 3-valued logic. (In 3-valued logic a statement can be either true, false, or neither.) In principle, you can build computers out of any $n$-valued logic. There are also computers based upon infinite-valued logic. Examples of such computers include fuzzy computers (based upon fuzzy logic) and quantum computers (based upon the laws of the quantum world!). There are so many interesting things to talk about these uncoventional computers but our discussion here is about conventional computers that are based upon propositional logic.

Computers carry out logical calculations. Arithmetic operations such as adding two numbers are in fact logical calculations as we will see later. Computers (conventional binary computers to be clear) can understand only the bits 0 (switch on-current) and 1 (switch off-no current). Hence everything in a computer is represented as patterns of of 0s and 1s. 0 and 1 can be understood as the two truth values, true and false, of propositional logic. For example, 0 could represent true while 1 does false. Using propositional logic one can design physical devices, called logic circuits, that perform intended results by producing bits (output) from bits (input). The design of logic circuits is called computer logic. The smallest units of a circuit are called the logic gates or gates in short, i.e. logic gates are building blocks of a logic circuit. Gates correspond to the operations of propositional logic, such as $\vee$, $\wedge$, $\oplus$, and $\neg$.

Example. The diagram of Or Gate.

Example. The diagram of And Gate.

Example. The diagram of Exclusive Or Gate.

Example. The diagram of Not Gate

In practice, however, not all these operations are available to a circuit designer. For example, exclusive or can be performed using $\vee$, $\wedge$ and $\neg$ as we have seen here. $$x\oplus y\equiv(x\wedge\neg y)\vee(\neg x\wedge y)$$ The following figure shows a logic circuit that computes $x\oplus y$. The semi circle on a wire represents that the wire is crossing over another i.e. they are not connected.

Not gate often simply represented by a bubble. With this convention, the above circuit can be simplified as in the following figure.

There is a very useful gate called NAND (NOT-AND) Gate. It is defined by nand operator $$p|q\equiv\neg(p\wedge q)$$ What’s interesting about nand operator is that any conventional operator can be expressed using only nand operator. For example, \begin{align*}\neg p&\equiv p|p\\p\wedge q&\equiv\neg(p|q)\equiv(p|q)|(p|q)\end{align*}

Example. The diagram of NAND Gate.

Binary Arithmetic

The basic rules of binary arithmetic: \begin{equation}\begin{aligned}0+0&=0\\0+1&=1\\1+0&=1\\1+1&=0,\ \mbox{carry}\ 1\end{aligned}\label{eq:binadd}\end{equation}As shown, when adding 1 to 1, the result is 0 but a 1 is carried into the next position to the left. For example,adding 1 to 10111 results in 11000 with three carries. $$\begin{array}{cccccc}& & 1 & 1 & 1 & \\& 1 & 0 & 1 & 1 & 1\\+& & & & & 1\\\hline & 1 & 1 & 0 & 0 & 0\end{array}$$ Here is another example $10101+01111$. \begin{equation}\begin{array}{ccccccc}& & 1 & 1 & 1 & 1 & \\& & 1 & 0 & 1 & 0 & 1\\+& & 0 & 1 & 1 & 1 & 1\\\hline & 1 & 0 & 0 & 1 & 0 & 0\end{array}\label{eq:binadd2}\end{equation} The question is how do we design hardware to do binary arithmetic? The simplest operation is the addition of two bits shown in \eqref{eq:binadd}. The equations in \eqref{eq:binadd} actually create two output bits, a sum $s$ and a carry $c$, from two input bits $x$ and $y$. The carry bit was not mentioned for the first three because it is 1 only when both input bits are 1. On the other hand, the sum is 1 only when one of the input bits is 1 and the other is 0. Hence, the device that performs the addition of two bits, called a half adder can be represented by the following diagram.

However, a half adder is not adequate to compute more complex binary sums such as \eqref{eq:binadd2} because when adding numbers with multiple digits we sometimes need three input bits. A full adder takes three input bits $X$, $Y$, and the carry-in bit $C_{\mathrm{in}}$ and produce two output bits, the sum $S$ and the carry-out bit $C_{\mathrm{out}}$. Th following is the truth table for computing the two output bits $S$ and $C_{\mathrm{out}}$ from the three input bits $X$, $Y$, and $C_{\mathrm{in}}$. $$\begin{array}{|c|c|c|c|c|}\hline X & Y & C_{\mathrm{in}} & S & C_{\mathrm{out}}\\\hline 0 & 0& 0 & 0 & 0\\\hline0 & 0 & 1 & 1 & 0\\\hline0 & 1 & 0 & 1 & 0\\\hline 0 & 1 & 1 & 0 &1\\\hline 1 & 0 & 0 & 1 &0\\\hline 1 & 0 & 1 & 0 & 1\\\hline 1 & 1 &0 & 0 &1\\\hline 1 & 1 & 1 & 1 & 1\\\hline\end{array}$$ The following diagram shows a way to construct a full adder using two half adders (represented by a box called HA). The circuit produces the sum bit by adding $X$ and $Y$ and then adding $C_{\mathrm{in}}$ to the result. The $C_{\mathrm{out}}$ is 1 if there is a carry from either the first or the second of these additions.

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019

In this note, we study some standard ways (normal forms) of representing formulas. The rules are:

1. Only $\wedge$, $\vee$, and $\neg$ are used.
2. Any negations are attached to propositional variables, not to larger expressions.
3. The $\vee$’s and the $\wedge$’s are organized in the manner described below: A literal is either a propositional variable (such as $p$) or the negation of a single variable (such as $\neg q$). If a formula is an $\wedge$ of $\vee$’s of literals we say it is in CNF (Conjunctive Normal Form). For example, \begin{align*}(p\vee q)\wedge(\neg p\vee q)\wedge(p\vee\neg q)\wedge(\neg p\vee \neg q)\\p\wedge\neg p\\(p\vee\neg q\vee r)\wedge(\neg s\vee t)\end{align*} are all in CNF. One may wonder why $p\wedge\neg p$ is in CNF. That’s because it is logically equivalent to $(p\vee p)\wedge(\neg p\vee\neg p)$. A formula is in DNF (Disjunctive Normal Form), on the other hand, is an $\vee$ of $\wedge$’s of literals. For example, $$(p\wedge\neg q\wedge r)\vee(\neg r\wedge t)$$ is in DNF. $p\wedge\neg p$ is also in DNF because it is logically equivalent to $(p\wedge\neg p)\vee (p\wedge\neg p)$. Similarly, $p\vee q$ is in both CNF and DNF.

Example. $(p\vee\neg q\vee r)\wedge(\neg q\vee t)$ is in CNF. Formulae $p\vee\neg q\vee r$ and $\neg q\vee t$ are clauses of the formula. The clauses of a CNF formula are disjuncts of literals while the clauses of a DNF formula are conjuncts of literals. That is to say, a CNF formula is a conjunction of disjuncts of literals and a DNF formula is a disjunction of conjuncts of literals.

A CNF formula is true if at least one literal from each clause is true. Similarly, a DNF formula is true if and only of there is at least one disjunct (clause) in which all the literals are true. For example, the DNF formula $$(\neg p\wedge q)\vee(p\wedge r)$$ is true when $p$ is false and $q$ is true.

Theorem. (De Morgan’s Law) \begin{align*}\neg(p\wedge q)&\equiv\neg p\vee\neg q\\\neg(p\vee q)&\equiv\neg p\wedge\neg q\end{align*}

Proof. It can be easily proved by truth table. We prove only the first one here. The proof of the second one is left for exercise. $$\begin{array}{|c|c|c|c|c|c|c|}\hline p & q & p\wedge q &\neg(p\wedge q) & \neg p & \neg q & \neg p\vee\neg q\\\hline T & T & T & F & F & F &F\\\hline T & F & F & T &F & T & T\\\hline F & T & F & T & T & F & T\\\hline F & F & F & T & T & T & T\\\hline\end{array}$$

Example. Using commutative laws, associative laws, distributive laws we learned here along with De Morgan’s law, we can write a given formula into its equivalent formula in a normal form. To see this let us consider the formula $$p\vee(q\wedge(r\vee(s\wedge t)))$$ It can be written into an equivalent formula in conjunctive normal form. \begin{align*}p\vee(q\wedge(r\vee(s\wedge t)))&\equiv (p\vee q)\wedge(p\vee(r\vee(s\wedge t))\\&\equiv(p\vee q)\wedge(p\vee((r\vee s)\wedge(r\vee t))\\&\equiv(p\vee q)\wedge(p\vee(r\vee s))\wedge(p\vee(r\vee t))\\&\equiv(p\vee q)\wedge(p\vee r\vee s)\wedge(p\vee r\vee t)\end{align*} But then it can also be written into an equivalent formula in disjunctive normal form. \begin{align*}p\vee(q\wedge(r\vee(s\wedge t)))&\equiv p\vee((q\wedge r)\vee(q\wedge(s\wedge t)))\\&\equiv p\vee(q\wedge r)\vee(q\wedge s\wedge t)\end{align*} In general, the following theorem holds.

Theorem. Every formula is equivalent to one in conjunctive normal form, and also to one in disjunctive normal form.

We are not going to prove the theorem here but interesting readers can find a proof in the reference [1] below.

Example. Write $(\neg p\vee q)\Longrightarrow\neg p$ in disjunctive normal form.

Solution. \begin{align*}(\neg p\vee q)\Longrightarrow\neg p&\equiv\neg(\neg p\vee q)\vee\neg q\\&\equiv(\neg\neg p\wedge\neg q)\vee\neg q\\&\equiv p\vee\neg q\vee\neg q\\&\equiv p\vee\neg p\vee\neg q\end{align*} Since $p\vee\neg p$ is a tautology, $(\neg p\vee q)\Longrightarrow\neg p$ is a tautology.

As shown in the above example, any expression that can be simplified to become a tautology must be a tautology itself. Determining whether a formula is a tautology is a fundamental problem of computer science. Using truth table is in deed not an effective method to tackle the problem because the truth table of a formula with a large number of variables would become too big to handle for us. For instance, the truth table for a formula with 30 variables would have $2^{30}=1,073,741,824$ rows, more than a billion rows! It is yet unknown if there is an effective algorithm to determine satisfiability, in particular whether a formula is a tautology.

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019

A proposition is a statement that is either true or false. We can combine one or more propositions to create more complicated propositions using conjunctions. Those conjunctions include:

1. Negation: $\neg p$, meaning not $p$.
2. Inclusive Or: $p\vee q$, meaning $p$ or $q$ (could be both).
3. And: $p\wedge q$, meaning $p$ and $q$.
4. Exclusive Or: $p\oplus q$, meaning either $p$ or $q$.
5. Implies: $p\Longrightarrow q$, meaning if $p$ then $q$ ($p$ implies $q$). $p$ and $q$ are called the hypothesis and the conclusion, respectively.
6. Equivalence: $p\Longleftrightarrow q$, meaning $p$ if and only if $q$. $p\Longleftrightarrow q$ is shorthand for $(p\Longrightarrow q)\wedge(p\Longleftarrow q)$.

Definition. A propositional formula is defined by the following.

PF1. Any propositional variable (such as $p$ and $q$) is a formula.

PF2. If $\alpha$ and $\beta$ are formulas, so are

1. $\alpha\vee\beta$
2. $\alpha\wedge\beta$
3. $\neg\alpha$

For example $\neg(p\vee q)$ is a formula.

Truth Tables

The truth value of a formula can be found by its truth table. A formula is said to be satisfiable if at least one truth assignment satisfies it. A formula is called a tautology if every truth assignment satisfies it. A formula is said to be unsatisfiable if no truth assignment satisfies it.

Here are some examples.

1. The truth table of $\neg p$ $$\begin{array}{|c|c|}\hline p & \neg p\\\hline T & F\\\hline F & T\\\hline\end{array}$$
2. The truth table of $p\wedge q$ $$\begin{array}{|c|c|c|}\hline p & q & p\wedge q\\\hline T & T & T\\\hline T & F & F\\\hline F & T & F\\\hline F & F & F\\\hline\end{array}$$
3. The truth table of $p\wedge\neg p$. $$\begin{array}{|c|c|c|}\hline p & \neg p & p\wedge\neg p\\\hline T & F & F\\\hline F & T & F\\\hline\end{array}$$ $p\wedge\neg p$ is unsatisfiable.
4. The truth table of $p\vee q$ $$\begin{array}{|c|c|c|}\hline p & q & p\vee q\\\hline T & T & T\\\hline T & F & T\\\hline F & T & T\\\hline F & F & F\\\hline\end{array}$$
5. The truth table of $p\vee\neg p$. $$\begin{array}{|c|c|c|}\hline p & \neg p & p\vee\neg p\\\hline T & F & T\\\hline F & T & T\\\hline\end{array}$$ $p\vee\neg p$ is a tautology.
6. The truth table of $p\oplus q$ $$\begin{array}{|c|c|c|}\hline p & q & p\oplus q\\\hline T & T & F\\\hline T & F & T\\\hline F & T & T\\\hline F & F & F\\\hline\end{array}$$
7. The truth table of $p\Longrightarrow q$ $$\begin{array}{|c|c|c|}\hline p & q & p\Longrightarrow q\\\hline T & T & T\\\hline T & F & F\\\hline F & T & T\\\hline F & F & T\\\hline\end{array}$$ It must be puzzling for readers as to why a false hypothesis can imply anything. Remember that we are doing propositional logic and any statement of our concern should be either true or false. So it comes down to the decision on what truth value to assign to a conditional statement with false hypothesis. If we were to assign the truth value F, all hell will break loose. Here is why. Consider the conditional statement “if $p$ then $\neg p$” and assume that $p$ is false. That must mean $\neg p$ is true since $p$ is a proposition. However, we decided to assign the truth value $F$ to the conditional statement hence $\neg p$ must also be false. This is a contradiction! To avoid this sort of disastrous contradiction, we should assign the truth value T to a conditional statement with false hypothesis. We claimed without a proof that the empty set is a subset of every set here. The statement “$x\in\emptyset\Longrightarrow x\in A$” is always true because the hypothesis $x\in\emptyset$ is false. Hence $\emptyset\subseteq A$ for any set $A$.
8. The truth value of $p\Longleftrightarrow q$. $$\begin{array}{|c|c|c|c|c|}\hline p & q & p\Longrightarrow q & p\Longleftarrow q & p\Longleftrightarrow q\\\hline T & T & T & T & T\\\hline T & F & F & T & F\\\hline F & T & T & F & F\\\hline F & F & T & T & T\\\hline\end{array}$$
9. The truth value of $p\wedge q\Longrightarrow r$. $$\begin{array}{|c|c|c|c|c|}\hline p & q & r & p\wedge q & p\wedge q\Longrightarrow r\\\hline T & T & T & T & T\\\hline T & T & F & T & F\\\hline T & F & T & F & F\\\hline T & F & F & F & T\\\hline F & T & T & F & T\\\hline F & T & F & F & T\\\hline F & F & T & F & T\\\hline F & F & F & F & T\\\hline\end{array}$$

When two fomulae $\alpha$ and $\beta$ have the same truth table, we say $\alpha$ is logically equivalent to $\beta$ and write $\alpha\equiv\beta$.

Theorem. $p\Longrightarrow q\equiv\neg p\vee q$.

Proof. $$\begin{array}{|c|c|c|c|c|}\hline p & q & p\Longrightarrow q & \neg p & \neg p\vee q\\\hline T & T & T & F & T\\\hline T & F & F & F & F\\\hline F & T & T & T & T\\\hline F & F & T & T & T\\\hline\end{array}$$

Theorem. $p\oplus q\equiv(p\wedge\neg q)\vee(\neg p\wedge q)$.

Proof. Left to readers as an exercise.

$\vee$ and $\wedge$ can be considered as operations on formulae and the following laws hold:

Commutative Laws. For any formulae $\alpha$ and $\beta$, \begin{align*}\mbox{(CL1)}\ \alpha\vee\beta&\equiv\beta\vee\alpha\\\mbox{(CL2)}\ \alpha\wedge\beta&\equiv\beta\wedge\alpha\end{align*}

Associative Laws. For any formulae $\alpha$, $\beta$ and $\gamma$, \begin{align*}\mbox{(AL1)}\ (\alpha\vee\beta)\vee\gamma&\equiv\alpha\vee(\beta\vee\gamma)\\\mbox{(AL2)}\ (\alpha\wedge\beta)\wedge\gamma&\equiv\alpha\wedge(\beta\wedge\gamma)\end{align*}

Distributive Laws. For any formulae $\alpha$, $\beta$ and $\gamma$, \begin{align*}\mbox{(DL1)}\ \alpha\vee(\beta\wedge\gamma)&\equiv(\alpha\vee\beta)\wedge(\alpha\vee\gamma)\\\mbox{(DL2)}\ \alpha\wedge(\beta\vee\gamma)&\equiv(\alpha\wedge\beta)\vee(\alpha\wedge\gamma)\end{align*}

These laws can be used to show two formulae are logically equivalent without using truth table. Proof by a truth table can be really cumbersome when concerned formulae are complicated.

References.

[1] Essential Discrete Mathematics for Computer Science, Harry Lewis and Rachel Zax, Princeton University Press, 2019