Let us begin with the following definition.
Definition. Let ${\bf u}=(u_1,u_2,u_3)$ and ${\bf v}=(v_1,v_2,v_3)$. Then the dot product ${\bf u}\cdot{\bf v}$ is defined by $${\bf u}\cdot{\bf v}=u_1v_1+u_2v_2+u_3v_3$$
The name “product” is misleading as it is not really an operation. The reason is simple because the outcome of a dot product is a scalar, not a vector. So what is a big deal about this dot product? The dot product defines the length of a vector. Let ${\bf u}=(u_1,u_2,u_3)$. Then $$|{\bf u}|=\sqrt{{\bf u}\cdot {\bf u}}=\sqrt{u_1^2+u_2^2+u_3^3}$$ Furthermore it can also define the distance between two points in space as shown in Figure 1:
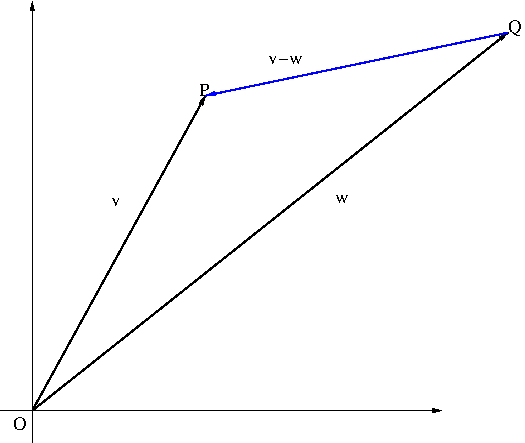
Let two position vectors ${\bf v}=(v_1,v_2,v_3)$ and ${\bf w}=(w_1,w_2.w_3)$ respectively represent points $P$ and $Q$ in space. The the distance $\overline{PQ}$ between the two points $P$ and $Q$ is the length of the vector ${\bf v}-{\bf w}$ $$\overline{PQ}=|{\bf v}-{\bf w}|=\sqrt{({\bf v}-{\bf w})\cdot({\bf v}-{\bf w})}=\sqrt{(v_1-w_1)^2+(v_2-w_2)^2+(v_3-w_3)^2}$$
Example. \begin{align*}(2,4)\cdot(3,-1)&=2(3)+4(-1)=2\\(-1,7,4)\cdot\left(6,2,-\frac{1}{2}\right)&=-1(6)+7(2)+4\left(-\frac{1}{2}\right)=6\\({\bf i}+2{\bf j}-3{\bf k})\cdot(2{\bf j}-{\bf k})&=1(0)+2(2)+(-3)(-1)=7\end{align*}
The dot product satisfies the following properties. These properties can be easily verified from its definition.
Theorem. Let ${\bf u}$, ${\bf v}$ and ${\bf w}$ be vectors in space and $c$ a scalar. Then
- ${\bf u}\cdot{\bf v}={\bf v}\cdot{\bf u}$
- ${\bf u}\cdot ({\bf v}+{\bf w})={\bf u}\cdot{\bf v}+{\bf u}\cdot{\bf w}$
- $(c{\bf u})\cdot{\bf v}=c({\bf u}\cdot{\bf v})={\bf u}\cdot(c{\bf v})$
- ${\bf 0}\cdot {\bf u}=0$
Although this is beyond the scope of our discussion here, I would like to mention that the notion of the dot product can be generalized so that it can give rise to a different kind of length. Such generalization is called a scalar product or an inner product. You can read more about it here in case you are interested. A scalar product would satisfy the properties 1-4 in the above theorem. The dot product is associated with the length we are most familiar with, called the Euclidean length but that is not the only kind of length out there. For example, in the vector space of continuous functions on the closed interval $[0,1]$ (which was mentioned here), the scalar product of two functions $f$ and $g$, denoted by $\langle f,g\rangle$ is defined by $$\langle f,g\rangle=\int_0^1 f(x)g(x)dx$$ and the length of $f$ is defined by $$|f|=\sqrt{\langle f,f\rangle}=\sqrt{\int_0^1|f(x)|^2dx}$$ This type of a scalar product plays a very important role in quantum mechanics. It is used to measure the probability of a particle (such as an electron) to be in a particular quantum mechanical state.
There is an alternative description of the dot product.
Theorem. If $\theta$ is the angle between the vectors ${\bf u}$ and ${\bf v}$, where $0\leq\theta\leq\pi$, then \begin{equation}\label{eq:dotproduct}{\bf u}\cdot{\bf v}=|{\bf u}||{\bf v}|\cos\theta\end{equation}
Proof. By applying the Law of Cosines to triangle $\triangle OPQ$ in Figure 1, we obtain \begin{equation}\label{eq:lawcosine}|{\bf u}-{\bf v}|^2=|{\bf u}|^2+|{\bf v}|^2-2|{\bf u}||{\bf v}|\cos\theta\end{equation} \begin{align*}|{\bf u}-{\bf v}|^2&=({\bf u}-{\bf v})\cdot({\bf u}-{\bf v})\\&={\bf u}\cdot{\bf u}-{\bf u}\cdot{\bf v}-{\bf v}\cdot{\bf u}+{\bf v}\cdot{\bf v}\\&=|{\bf u}|^2-2{\bf u}\cdot{\bf v}+|{\bf v}|^2\end{align*}Replacing $|{\bf u}-{\bf v}|^2$ in \eqref{eq:lawcosine} by this last expression results in $$|{\bf u}|^2-2{\bf u}\cdot{\bf v}+|{\bf v}|^2=|{\bf u}|^2+|{\bf v}|^2-2|{\bf u}||{\bf v}|\cos\theta$$ and this simplifies to $${\bf u}\cdot{\bf v}=|{\bf u}||{\bf v}|\cos\theta$$
Example. Find the angle between the vector ${\bf u}=(2,2,-1)$ and ${\bf v}=(5,-3,2)$.
Solution. From \eqref{eq:dotproduct}, \begin{align*}\cos\theta&=\frac{{\bf u}\cdot{\bf v}}{|{\bf u}||{\bf v}|}\\&=\frac{2(5)+2(-3)+(-1)(2)}{\sqrt{2^2+2^2+(-1)^2}\sqrt{5^2+(-3)^2+2^2}}\\&=\frac{2}{3\sqrt{38}}\end{align*} Hence, $$\theta=\cos^{-1}\left(\frac{2}{3\sqrt{38}}\right)\approx 1.46\ \mathrm{rad}\ (84^\circ)$$
The alternative description of the dot product in \eqref{eq:dotproduct} is usually introduced as the definition of the dot product in high school/freshmen physics course.
From \eqref{eq:dotproduct}, we see that two vectors ${\bf u}$ and ${\bf v}$ are perpendicular or orthogonal (i.e. the angle $\theta$ between ${\bf u}$ and ${\bf v}$ is $\frac{\pi}{2}$) if and only if ${\bf u}\cdot{\bf v}=0$.
Example. $2{\bf i}+2{\bf j}-{\bf k}$ is perpendicular to $5{\bf i}-4{\bf j}+2{\bf k}$ because $$(2{\bf i}+2{\bf j}-{\bf k})\cdot(5{\bf i}-4{\bf j}+2{\bf k})=2(5)+2(-4)+(-1)(2)=0$$
This is beyond the scope of our discussion here but the notion of orthogonality of two vectors can be extended to higher dimensional spaces or more abstract vector spaces by defining that: two vectors ${\bf u}$ and ${\bf v}$ are said to be orthogonal if $\langle{\bf u},{\bf v}\rangle=0$, where $\langle\ ,\ \rangle$ denotes a scalar product. In our case, $\langle{\bf u},{\bf v}\rangle={\bf u}\cdot{\bf v}$. For example, Let $V$ be the set of all continuous functions on the closed interval $[-1,1]$. Then $V$ is a vector space with addition and scalar multiplication defined in the usual way that I discussed here. Also $\langle\ ,\ \rangle$ defined by $$\langle f,g\rangle=\int_{-1}^1f(x)g(x)dx$$ for $f,g\in V$ is a scalar product. The two functions $\sin(2n\pi x)$ and $\cos(2n\pi x)$ are continuous on $[-1,1]$ so they belong to $V$ i.e. they are vectors. They are also orthogonal because $$\langle\sin(2n\pi x),\cos(2n\pi x)\rangle=\int_{-1}^1\sin(2n\pi x)\cos(2n\pi x)dx=0$$
Let us take a look at Figure 2.
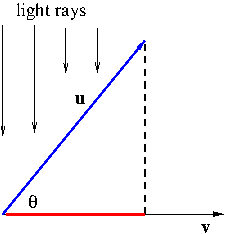
Imagine that light rays coming down on the vector ${\bf u}$ at the direction perpendicular to the vector ${\bf v}$. The the shadow of ${\bf u}$ will be cast on ${\bf v}$ (the red line segment in Figure 2). Mathematically, this shadow is called the orthographic projection of ${\bf u}$ onto ${\bf v}$. In fact, the red line segment is the orthographic projection of the length of the vector ${\bf u}$ onto ${\bf v}$. We denote it by $\mathrm{comp}_{\bf v}{\bf u}$ and call it the scalar projection of ${\bf u}$ onto ${\bf v}$. Using basic trigonometry, we can easily find that $$\mathrm{comp}_{\bf v}{\bf u}=|{\bf u}|\cos\theta$$ However, we prefer to express the scalar projection free of the angle $\theta$ i.e. in terms of only ${\bf u}$ and ${\bf v}$. This can be done using \eqref{eq:dotproduct}: \begin{align*}\mathrm{comp}_{\bf v}{\bf u}&=|{\bf u}|\cos\theta\\&=|{\bf u}|\frac{{\bf u}\cdot{\bf v}}{|{\bf u}||{\bf v}|}\\&=\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|}\end{align*} Hence we obtained our preferred form of the scalar projection \begin{equation}\label{eq:scalarprojection}\mathrm{comp}_{\bf v}{\bf u}=\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|}\end{equation} One can also consider the vector projection of ${\bf u}$ onto ${\bf v}$. All you have to do is to multiplying the scalar projection \eqref{eq:scalarprojection} by the direction of ${\bf v}$: \begin{equation}\label{eq:vectorprojection}\mathrm{proj}_{\bf v}{\bf u}=\mathrm{comp}_{\bf v}{\bf u}\frac{{\bf v}}{|{\bf v}|}=\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|^2}{\bf v}\end{equation}
Example. Find the scalar projection and the vector projection of ${\bf u}=(1,1,2)$ onto ${\bf v}=(-2,3,1)$.
Solution. The scalar projection is $$\mathrm{comp}_{\bf v}{\bf u}=\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|}=\frac{1(-2)+1(3)+2(1)}{\sqrt{(-2)^2+3^2+1^2}}=\frac{3}{\sqrt{14}}$$ The direction of ${\bf v}$ is $\frac{1}{\sqrt{14}}(-2,3,1)$. Hence, the vector projection is $$\mathrm{proj}_{\bf v}{\bf u}=\mathrm{comp}_{\bf v}{\bf u}\frac{1}{\sqrt{14}}(-2,3,1)=\frac{3}{14}(-2,3,1)=\left(-\frac{3}{7},\frac{9}{14},\frac{3}{14}\right)$$
Consider a vector ${\bf v}=(v_1,v_2,v_3)$ in space. The angle $\alpha$ between ${\bf v}$ and ${\bf i}$, the angle $\beta$ between ${\bf v}$ and ${\bf j}$, and the angle $\gamma$ between ${\bf v}$ and ${\bf k}$ are called the direction angles of ${\bf v}$. (See Figure 3.)
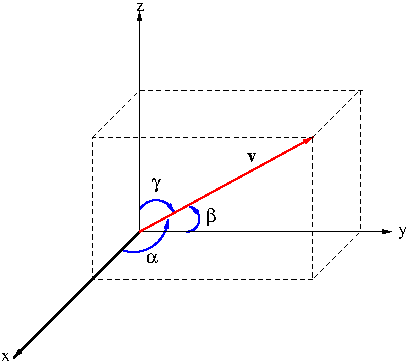
Now, \begin{equation}\begin{aligned}\cos\alpha&=\frac{{\bf v}\cdot{\bf i}}{|{\bf v}||{\bf i}|}=\frac{v_1}{|{\bf v}|}\\\cos\beta&=\frac{{\bf v}\cdot{\bf j}}{|{\bf v}||{\bf j}|}=\frac{v_2}{|{\bf v}|}\\\cos\gamma&=\frac{{\bf v}\cdot{\bf k}}{|{\bf v}||{\bf k}|}=\frac{v_3}{|{\bf v}|}\end{aligned}\label{eq:directioncosine}\end{equation} $\cos\alpha$, $\cos\beta$ and $\cos\gamma$ are called the direction cosines of vector ${\bf v}$. It follows from \eqref{eq:directioncosine} that $(\cos\alpha,\cos\beta,\cos\gamma)$ is the direction of ${\bf v}$, hence the name directions cosines.
Example. Find the direction angles of the vector ${\bf v}=(1,2,3)$.
Solution. $|{\bf v}|=\sqrt{1^2+2^2+3^2}=\sqrt{14}$. Using \eqref{eq:directioncosine}, we have \begin{align*}\alpha&=\cos^{-1}\left(\frac{1}{\sqrt{14}}\right)\approx 74^\circ\\\beta&=\cos^{-1}\left(\frac{2}{\sqrt{14}}\right)\approx 58^\circ\\\gamma&=\cos^{-1}\left(\frac{3}{\sqrt{14}}\right)\approx 37^\circ\end{align*}
Work
Consider a linear motion i.e. a motion of an object along a straight line. See Figure 4.
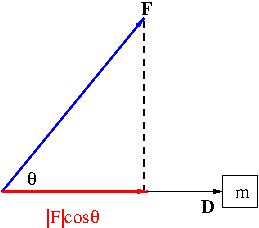
Suppose that an object is moved by a force ${\bf F}$. If the displacement is ${\bf D}$, then the work $W$ done by this force ${\bf F}$ is defined by the scalar projection of ${\bf F}$ onto ${\bf D}$, $|{\bf F}|\cos\theta$ (this is the component of ${\bf F}$ that actually moved the object) times the distance moved $|{\bf D}|$: \begin{equation}\label{eq:work}W={\bf F}\cdot{\bf D}\end{equation}
Example. A wagon is pulled a distance of 100 m along a horizontal path by a constant force of 70 N. The handle of the wagon is held at an angle of $35^\circ$ above the horizontal. Find the work done by the force.
Solution. The force ${\bf F}$ and the displacement ${\bf D}$ are as depicted in Figure 5.
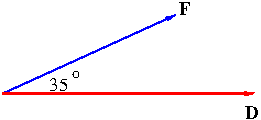
Thus the work $W$ is \begin{align*}W&={\bf F}\cdot{\bf D}=|{\bf F}||{\bf D}|\cos 35^\circ\\&=70(100)\cos 35^\circ=5734\ \mathrm{J}\end{align*} where J, called Joule, is a unit for work which stands for Newton times meter.
Example. A force given by the vector ${\bf F}=3{\bf i}+4{\bf j}+5{\bf k}$ moves a particle from the point $P(2,1,0)$ to the point $Q(4,6,2)$. Find the work done by the force.
Solution. Here, there is no mention of a particular path the particle is taking. We assume that the motion is again linear. The displacement is ${\bf D}=\overrightarrow{PQ}=(4-2,6-1,2-0)=(2,5,2)$. Hence the work is \begin{align*}W&={\bf F}\cdot{\bf D}=(3,4,5)\cdot(2,5,2)\\&=6+20+10=36\end{align*}
Examples in this note have been taken from [1].
References.
[1] Calculus, Early Transcendentals, James Stewart, 6th Edition, Thompson Brooks/Cole
