What is a vector?
A vector is a quantity that has both direction and magnitude. Examples of vectors include displacement, velocity, force, weight, momentum, etc. A quantity that has only magnitude is called a scalar. Scalars are really just numbers. Examples of scalars include distance, speed, mass, temperature, etc. Since a vector has both direction and magnitude, it can be visually represented by a directed arrow. For instance, if a particle moves from a point $A$ to another point $B$, its displacement (i.e. the shortest distance from $A$ to $B$) is denoted by $\overrightarrow{AB}$ and it is visually represented by a directed arrow as in Figure 1.
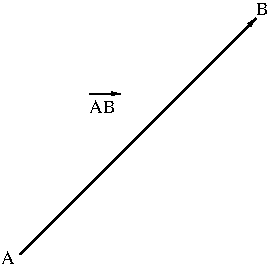
The direction at which the arrow is pointing is the direction of the vector $\overrightarrow{AB}$ and the length of the arrow is the magnitude of the vector $\overrightarrow{AB}$. When it is not necessary to specify the initial point and the terminal point, a vector is denoted by a lower case alphabet letter with arrow on top like $\vec v$ or in boldface like ${\bf v}$.
Two vectors are said to be the same or equivalent if they have the same direction and the magnitude regardless of where they are located. If vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ are the same, we write $\overrightarrow{AB}=\overrightarrow{CD}$. Figure 2 shows two equivalent vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$.
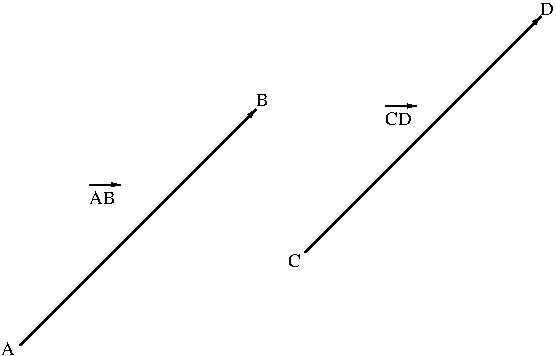
The equivalence of two vectors implies that a vector can be moved around maintaining its characters (direction and magnitude) so it stays as the same vector although its location has changed (meaning its initial and terminal points have changed). Moving a vector without changing direction and magnitude is called a parallel translation.
There are two types of operations on vectors. One is vector addition and the other is scalar multiplication. Vector addition is defined pictorially by using a parallelogram or a triangle. Figure 3 shows vector addition $$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$$ by using a parallelogram.
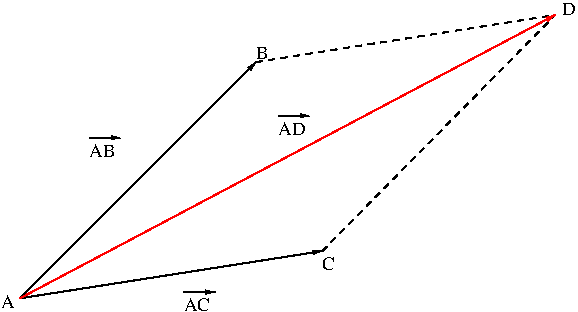
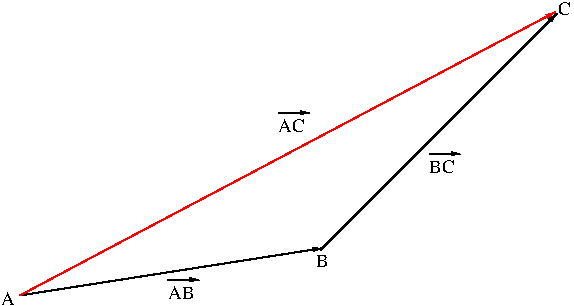
Figure 4 shows vector addition $$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$$ by using a triangle. The two ways of adding two vectors are indeed equivalent. The only difference is how you locate two vectors to add them together.
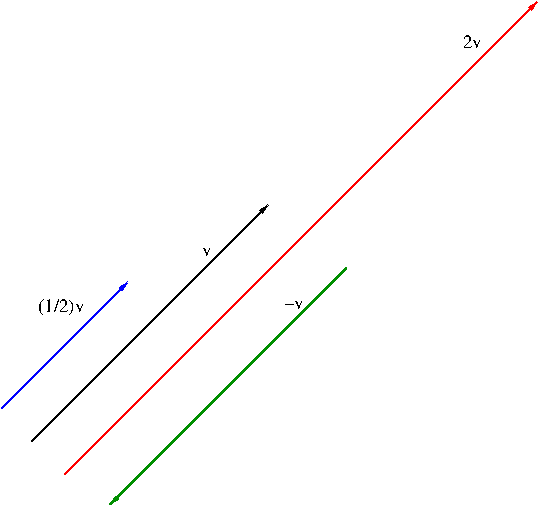
Scalar multiplication is a product between a scalar and a vector. While many people, even some (less careful) mathematicians, consider it as an operation, it is not an operation but an action. I am not going to talk about what an action is here. In case someone is curious, you can visit the Wikipedia page on Group Action here. In calculus level, distinction between an operation and an action is not really important at all. Let $c$ be a scalar and $v$ a vector. What the scalar multiplication $c{\bf v}$ does is, depends on the value of $c$, it can stretch (when $c>1$), shrink (when $0<c<1$), or reverse the direction (when $c=-1$) of vector ${\bf v}$ as illustrated in Figure 5.
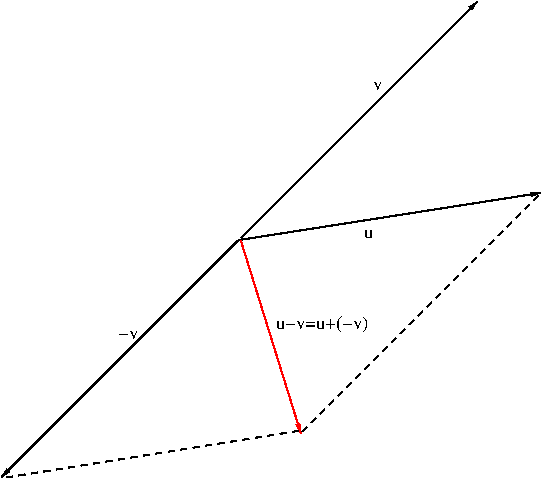
Using vector addition and scalar multiplication, one can define subtraction of a vector ${\bf v}$ from another vector ${\bf u}$: $${\bf u}-{\bf v}:={\bf u}+(-{\bf v})$$ See Figure 6.
Earlier I mentioned that a vector can be moved around while preserving its direction and magnitude, and a parallel translation of a vector is still considered to be the same as the previous vector, although it is now at a different location. Among all those same vectors, we are particularly interested in vectors that are starting the origin $O$. Figure 7 shows an example of such a vector.
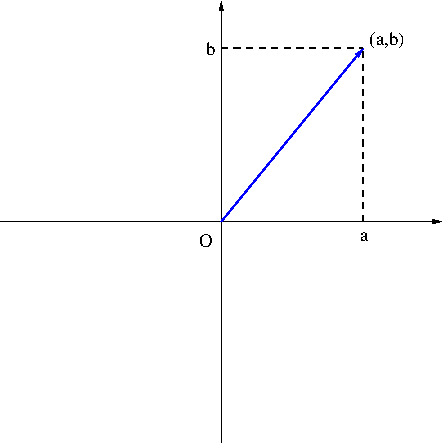
A vectors whose initial point is the origin $O$ is called a position vector or a located vector. A position vector is determined only by its terminal point, thereby it can be identified with a point in space and conversely a point in space can be identified with a position vector. For example, if the terminal point of a position vector ${\bf v}$ is $(a_1,a_2,a_3)$, then we regard them the same i.e. ${\bf v}=(a_1,a_2,a_3)$. Why this is such a big deal? The directed arrow representation of a vector has a lot of limitations. The most severe limitation is that it can only be useful when we can see them, i.e. their usage is limited within 3-dimensions as our perception does not allow us to go beyond 3-dimensions. However, Einstein’s theory of relativity (which has also been confirmed by numerous experiments and observations) that our universe is actually 4-dimensional. But that’s the universe we observe right now. String theory tells us that the universe can have up to 26-dimensions. It does not have to go that far beyond though. There are many other places here down on earth including computer science, economics, etc. where the notions of vectors in higher dimensions are being used. Considering position vectors resolve the limitation. Furthermore, now that we identify vectors with points in space and points are represented by ordered $n$-tuples (ordered pairs, triples, quadruples, depending on the dimension of the space) which are algebraic objects, we can use the power of algebra to describe the properties of vectors.
Given the points $A(a_1,a_2,a_3)$ and $B(b_1,b_2,b_3)$, the vector ${\bf v}$ which is represented by the directed arrow $\overrightarrow{AB}$ is $${\bf v}=(b_1-a_1,b_2-a_2,b_3-a_3)$$
Example. Find the vector represented by the directed arrow with initial point $A(2,-3,4)$ and $B(-2,1,1)$.
Solution. ${\bf v}=(-2-2,1-(-3),1-4)=(-4,4,-3)$.
The length or magnitude of a vector ${\bf v}$ is denoted by $|{\bf v}|$. For a vector ${\bf v}=(v_1,v_2)$ in the plane, $|{\bf v}|$ is given by $$|{\bf v}|=\sqrt{v_1^2+v_2^2}$$ (It’s easy to see this from Figure 7 using the Pythagorean law.) Similarly, for a vector ${\bf v}=(v_1,v_2,v_3)$ in space, $$|{\bf v}|=\sqrt{v_1^2+v_2^2+v_3^3}$$ It follows from the definition that \begin{equation}\label{eq:length}|c{\bf v}|=|c||{\bf v}|\end{equation} where $c$ is a scalar.
Vector addition and scalar multiplication can be nicely defined algebraically without using parallelograms or triangles. Furthermore, these algebraic definitions apply to vectors in arbitrary $n$-dimensional space. For vectors ${\bf u}=(u_1,u_2,u_3)$, ${\bf v}=(v_1,v_2,v_3)$ and a scalar $c$, \begin{align*}{\bf u}+{\bf v}&:=(u_1+v_1,u_2+v_2,u_3+v+3)\\c{\bf u}&:=(cu_1,cu_2,cu_3)\end{align*}
Example. If ${\bf u}=(4,0,3)$ and ${\bf v}=(-2,1,5)$, find $|{\bf u}|$, ${\bf u}+{\bf v}$, ${\bf u}-{\bf v}$, $3{\bf v}$, $2{\bf u}+5{\bf v}$.
Solution. \begin{align*}|{\bf u}|&=\sqrt{4^2+0^2+3^3}=\sqrt{25}=5\\{\bf u}+{\bf v}&=(4+(-2),0+1,3+5)=(2,1,8)\\{\bf u}-{\bf v}&=(4-(-2),0-1,3-5)=(6,-1,-2)\\3{\bf v}&=(3(-2),3(1),3(5))=(-6,3,15)\\2{\bf u}+5{\bf v}&=(2(4),2(0),2(3))+(5(-2),5(1),5(5))=(8,0,6)+(-10,5,25)=(-2,5,31)\end{align*}
Theorem. Let ${\bf u}$, ${\bf v}$, and ${\bf w}$ be vectors in $n$-dimensional space and $c$ and $d$ are scalars. Then
- ${\bf u}+{\bf v}={\bf v}+{\bf u}$
- ${\bf u}+({\bf v}+{\bf w})=({\bf u}+{\bf v})+{\bf w})$
- ${\bf u}+{\bf 0}={\bf u}$, where ${\bf 0}=(0,0,\cdots,0)$
- ${\bf u}+(-{\bf u})={\bf 0}$
- $c({\bf u}+{\bf v})=c{\bf u}+c{\bf v}$
- $(c+d){\bf u}=c{\bf u}+d{\bf u}$
- $(cd){\bf u}=c(d{\bf u})$
- $1{\bf u}={\bf u}$
It turns out the the original definition of vectors as quantities that have both direction and magnitude is quite obsolete and that even the definition of vectors by ordered $n$-tuples is not adequate enough to address much needed a broader notion of vectors arising in modern physics and engineering. For this reason, in modern treatment of vectors we no longer define what an individual vector is but instead we define a vector space. Simply speaking, a set $V$ with addition $+$ and scalar multiplication $\cdot$ satisfying the properties 1-8 is called a vector space, and the elements of $V$ are called vectors. Under this broader notion of vectors, things that were previously inconceivable to become vectors are now considered vectors. For example, $V$ the set of all continuous real-valued functions on the closed interval $[0,1]$ with addition $+$ and scalar multiplication $\cdot$ are defined by: \begin{align*}(f+g)(x)&:=f(x)+g(x)\\(cf)(x)&:=cf(x)\end{align*} for $f,g\in V$ and a scalar $c$. Then it is straightforward to show that the properties 1-8 are satisfied and therefore, $(V,+,\cdot)$ is a vector space and we regard continuous real-valued functions on $[0,1]$ as vectors. In fact, in quantum mechanics wave functions are state vectors. Another example is signal processing where functions are regarded as vectors. We are not going to delve into vector spaces further here. It is a main topic of linear algebra. For those who are curious, more examples of vector spaces can be found here.
There are infinitely many vectors. So it is humanly impossible to check if a certain property regarding vectors holds for all vectors. However there a particular finite set of vectors, called a basis, that constitute the entire vectors. A vector ${\bf u}=(u_1,u_2,u_3)$ can be written as \begin{equation}\label{eq:lincomb}{\bf u}=u_1(1,0,0)+u_2(0,1,0)+u_3(0,0,1)\end{equation} So we see that any vector can be represented by the three vectors $${\bf i}=(1,0,0),\ {\bf j}=(0,1,0),\ {\bf k}=(0,0,1)$$ by applying vector addition and scalar multiplication finitely many times as in \eqref{eq:lincomb}. The expression on the right hand side of the identity in \eqref{eq:lincomb} is called a linear combination or a superposition of ${\bf i}$, ${\bf j}$, ${\bf k}$. The three vectors ${\bf i}$, ${\bf j}$, ${\bf k}$ are called the canonical or standard basis vectors.
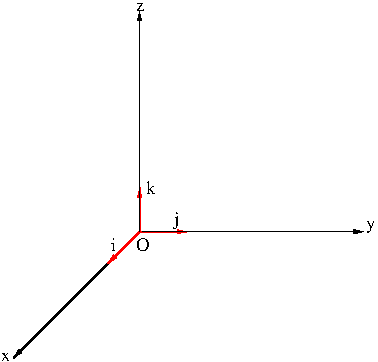
The number of standard basis vectors determines the dimension of the space. The dimension of a space is not necessarily finite though we are considering only finite dimensional spaces here (actually only 2- or 3-dimensional spaces). The set $V$ of all continuous functions on $[0,1]$ is infinite dimensional. The set of all state vectors in a quantum mechanics system is, in general, an infinite dimensional space called a Hilbert space.
Example. If ${\bf u}={\bf i}+2{\bf j}-3{\bf k}$ and ${\bf v}=4{\bf i}+7{\bf k}$, express $2{\bf u}+3{\bf v}$ in terms of ${\bf i}$, ${\bf j}$, ${\bf k}$.
Solution. \begin{align*}2{\bf u}+3{\bf v}&=2({\bf i}+2{\bf j}-3{\bf k})+3(4{\bf i}+7{\bf k})\\&=2{\bf i}+4{\bf j}-6{\bf k}+12{\bf i}+21{\bf k}\\&=14{\bf i}+4{\bf j}+15{\bf k}\end{align*}
Often in geometry and physics, we are only interested in the direction of a vector. A unit vector is a vector with length 1. Any non-zero vector can be re-scaled to a unit vector with the same direction. All that’s required is dividing the given vector by its magnitude. If ${\bf u}\ne {\bf 0}$, then $$\hat{\bf u}:=\frac{{\bf u}}{|{\bf u}|}$$ is a unit vector which has the same direction as ${\bf u}$: Using \eqref{eq:length}, $$|\hat{\bf u}|=\left|\frac{{\bf u}}{|{\bf u}|}\right|=\frac{1}{|{\bf u}|}|{\bf u}|=1$$
Example. Find the unit vector in the direction of the vector $2{\bf i}-{\bf j}-2{\bf k}$.
Solution. The length of the vector is $\sqrt{2^2+(-1)^2+(-2)^2}=\sqrt{9}=3$. Hence the unit vector with the same direction is $$\frac{2}{3}{\bf i}-\frac{1}{3}{\bf j}-\frac{2}{3}{\bf k}$$
In physics, when several forces are acting on an object, the resultant force or the net force experienced by the object is the vector sum of these forces.
Example. A 100-lb weight hangs from two wires as shown in Figure 9. Find the tension forces ${\bf T}_1$ and ${\bf T}_2$ in both wires and their magnitudes.
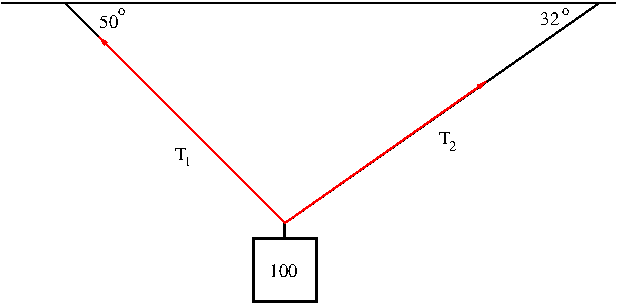
Solution. We first express the tensions ${\bf T}_1$ and ${\bf T}_2$ in terms of their horizontal and vertical components (the vectors in green in Figure 10).
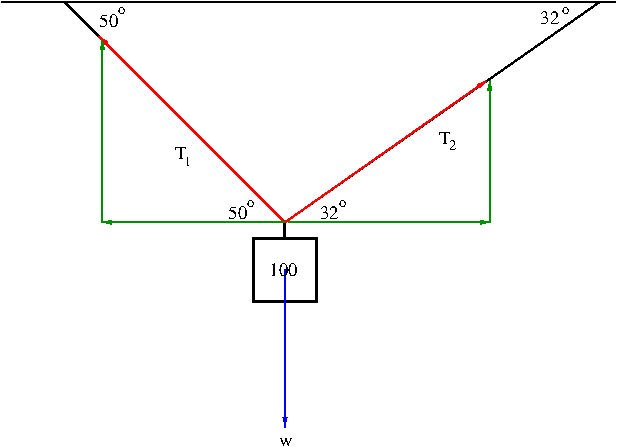
\begin{align}\label{eq:tension1}{\bf T}_1&=-|{\bf T}_1|\cos 50^\circ{\bf i}+|{\bf T}_1|\sin 50^\circ{\bf j}\\\label{eq:tension2}{\bf T}_2&=|{\bf T}_2|\cos 32^\circ{\bf i}+|{\bf T}_2|\sin 32^\circ{\bf j}\end{align} The net force ${\bf T}_1+{\bf T}_2$ of the tensions must counterbalance the weight ${\bf w}$ so that the mass stays hung as in the figure, i.e. $${\bf T}_1+{\bf T}_2=-{\bf w}=100{\bf j}$$ From equations \eqref{eq:tension1} and \eqref{eq:tension2}, we have $$(-|{\bf T}_1|\cos 50^\circ+|{\bf T}_2|\cos 32^\circ){\bf i}+(|{\bf T}_1|\sin 50^\circ+|{\bf T}_2|\sin 32^\circ){\bf j}=100{\bf j}$$ By comparing the components, we obtain the following equations: \begin{align*}-|{\bf T}_1|\cos 50^\circ+|{\bf T}_2|\cos 32^\circ&=0\\|{\bf T}_1|\sin 50^\circ+|{\bf T}_2|\sin 32^\circ&=100\end{align*} Solving these equations simultaneously we find \begin{align*}|{\bf T}_1|&=\frac{100}{\sin 50^\circ+\tan 32^\circ\cos 50^\circ}\approx 85.64\mathrm{lb}\\|{\bf T}_2|&=\frac{|{\bf T}_1|\cos 50^\circ}{\cos 32^\circ}\approx 64.91\mathrm{lb}\end{align*} Therefore, $${\bf T}_1\approx -55.05{\bf i}+65.60{\bf j},\ {\bf T}_2\approx 55.05{\bf i}+34.40{\bf j}$$
Examples in this note have been taken from [1].
References.
[1] Calculus, Early Transcendentals, James Stewart, 6th Edition, Thompson Brooks/Cole
