The First Derivative Test

The derivative $f'(x)$ can tell us a lot about the function $y=f(x)$. It can tell us where critical points are i.e. points at which $f'(x)=0$ and the critical points are likely places at which $y=f(x)$ assumes a local maximum or a local minimum values. By further examining the properties of $f'(x)$ we can also determine at which critical point, $f(x)$ assumes a local maximum, or a local minimum, or neither. But first we see that $f'(x)$ can tell us where $y=f(x)$ is increasing or decreasing.

Theorem. Increasing/Decreasing Test

1. If $f'(x)>0$ on an open interval, $f$ is increasing on that interval.
2. If $f'(x)<0$ on an open interval, $f$ is decreasing on that interval.

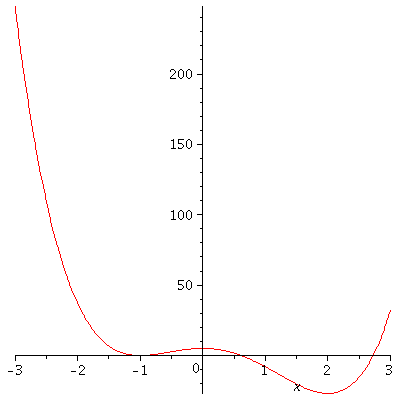
Example. Find where $f(x)=3x^4-4x^3-12x^2+5$ is increasing and where it is decreasing.

Solution.
\begin{align*}
f'(x)&=12x^3-12x^2-24x\\
&=12x(x^2-x-2)\\
&=12x(x-2)(x+1).
\end{align*}
The critical points are $x=-1,0,2$. Using, for instance, the test point method (which is the easiest method of solving an inequality), we obtain the following table.
$$
\begin{array}{|c|c|c|c|c|c|c|c|}
\hline
x & x<-1 & -1 & -1<x<0 & 0 & 0<x<2 & 2 & x>2\\
\hline
f'(x) & – & 0 & + & 0 & – & 0 & +\\
\hline
f(x) & \searrow & f(-1) & \nearrow & f(0) & \searrow & f(2) &\nearrow\\
\hline
\end{array}
$$
So we find that $f$ is increasing on $(-1,0)\cup(2,\infty)$ and $f$ is decreasing on $(-\infty,-1)\cup(0,2)$.

Now, local maximum values and local minimum values can be identified by observing the change of sign of $f'(x)$ at each critical point.

Theorem. [The First Derivative Test] Suppose that $c$ is a critical point of a differentiable function $f(x)$.

1. If the sign of $f'(x)$ changes from $+$ to $-$ at $c$, $f(c)$ is a local maximum.
2. If the sign of $f'(x)$ changes from $-$ to $+$ at $c$, $f(c)$ is a local minimum.
3. If the sign $f'(x)$ does not change at $c$, $f$ has neither a local maximum nor a local minimum at $c$.

Example. In the previous example, the sign of $f'(x)$ changes from $+$ to $-$ at $0$, so $f(0)=5$ is a local maximum. The sign of $f'(x)$ changes from $-$ to $+$ at $-1$ and at $2$, so $f(-1)=0$ and $f(2)=-27$ are local minimum values.

The following figure confirms our findings from the above two examples.

The Second Derivative Test

The second order derivative $f^{\prime\prime}(x)$ can provide us an additional piece of information on $y=f(x)$, namely the concavity of the graph of $y=f(x)$.

Definition. If the graph of $f$ lies above all of its tangents on an open interval $I$, it is called concave upward on $I$. If the graph of $f$ lies below all of its tangents on $I$, it is called concave downward on $I$.

From here on, $\smile$ denotes “concave up” and $\frown$ denotes “concave down”.

Definition. A point $(d,f(d))$ on the graph of $y=f(x)$ is called a point of inflection if the concavity of the graph of $f$ changes from $\smile$ to $\frown$ or from $\frown$ to $\smile$ at $(d,f(d))$. The candidates for the points of inflection may be found by solving the equation $f^{\prime\prime}(x)=0$ as shown in the example below.

Theorem. [Concavity Test]

1. If $f^{\prime\prime}(x)>0$ for all x in an open interval $I$, the graph of $f$ is concave up on $I$.
2. If $f^{\prime\prime}(x)<0$ for all x in an open interval $I$, the graph of $f$ is concave down on $I$.

Theorem. [The Second Derivative Test] Suppose that $f'(c)=0$ i.e. $c$ is a critical point of $f$. Suppose that $f^{\prime\prime}$ is continuous near $c$.

1. If $f^{\prime\prime}(c)>0$ then $f(c)$ is a local minimum.
2. If $f^{\prime\prime}(c)<0$ then $f(c)$ is a local maximum.

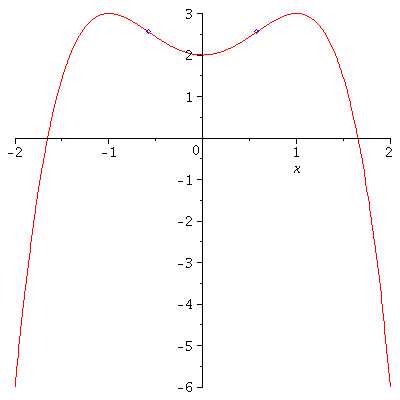
Example. Let $f(x)=-x^4+2x^2+2$.

1. Find and identify all local maximum and local minimum values of $f(x)$ using the Second Derivative Test.
2. Find the intervals on which the graph of $f(x)$ is concave up or concave down. Find all points of inflection.

Solution. 1. First we find the critical points of $f(x)$ by solving the equation $f'(x)=0$:
$$f'(x)=-4x^3+4x=-4x(x^2-1)=-4x(x+1)(x-1)=0.$$ So $x=-1,0,1$ are critical points of $f(x)$ Next, $f^{\prime\prime}(x)=-12x^2+4$. Since $f^{\prime\prime}(0)=4>0$ and $f^{\prime\prime}(-1)=f^{\prime\prime}(1)=-8<0$, by the Second Derivative Test, $f(0)=2$ is a local minimum value and $f(-1)=f(1)=3$ is a local maximum value.

2. First we need to solve the equation $f”(x)=0$:
$$f^{\prime\prime}(x)=-12x^2+4=-12\left(x^2-\frac{1}{3}\right)=-12\left(x+\frac{1}{\sqrt{3}}\right)\left(x-\frac{1}{\sqrt{3}}\right)=0.$$ So $f^{\prime\prime}(x)=0$ at $x=\pm\displaystyle\frac{1}{\sqrt{3}}$. By using the test-point method we find the following table:
$$
\begin{array}{|c||c|c|c|c|c|}
\hline
x & x<-\frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & x>\frac{1}{\sqrt{3}}\\
\hline
f^{\prime\prime}(x) & – & 0 & + & 0 & -\\
\hline
f(x) & \frown & f\left(-\frac{1}{\sqrt{3}}\right)=\frac{23}{9} & \smile & f\left(\frac{1}{\sqrt{3}}\right)=\frac{23}{9} & \frown\\
\hline
\end{array}
$$
The graph of $f(x)$ is concave down on the intervals $\left(-\infty,-\frac{1}{\sqrt{3}}\right)\cup\left(\frac{1}{\sqrt{3}},\infty\right)$ and is concave up on the interval $\left(-\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\right)$. The points of inflection are $\left(-\frac{1}{\sqrt{3}},\frac{23}{9}\right)$ and $\left(\frac{1}{\sqrt{3}},\frac{23}{9}\right)$.

The following figure confirms our findings from the above example.