Here is another math problem proposed by Sam Walters, one of my favorite mathematicians on Twitter.
Sam used a trigger word for me “isn’t hard.” I took it as being easy enough so any undergraduate math student can solve (turns out it actually is) which means I should be able to solve it in no time. I spent some hours to solve the functional equation $x^y=y^x$ but I was still stuck with my wounded ego until I saw a hint from another mathematician Rob Corless in his reply to the above tweet. The answer lies in Lambert W function! It is shame but I didn’t know Lambert W function though I have seen it. The function $f(x)=xe^x$ is injective (one-to-one) so it is invertible but one cannot explicitly write it’s inverse function so we denote it by $W(xe^x)$ i.e. $x=f^{-1}(xe^x)=W(xe^x)$. This $W$ is called Lambert W function. First let us take natural logarithm of the equation $x^y=y^x$. With some rearrangements, we arrive at \begin{equation}\label{eq:funeq}\frac{\ln y}{y}=\frac{\ln x}{x}\end{equation} Equation \eqref{eq:funeq} is well defined by the conditions $x,y>1$. Clearly $y=x$ is a solution. Now we want to find a less trivial solution. Let us introduce a new variable $u$ which satisfies $y=\frac{1}{u}$. Then \eqref{eq:funeq} is written in terms of $u$ as \begin{equation}\label{eq:funeq2}u\ln u=-\frac{\ln x}{x}\end{equation} Yet we introduce another variable $v$ which satisfies $u=e^v$. In terms of $v$, \eqref{eq:funeq2} is written as $f(v)=ve^v=-\frac{\ln x}{x}$ and hence $v=W\left(-\frac{\ln x}{x}\right)$ i.e. \begin{equation}\label{eq:funeq3}y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)\end{equation} The equation $v=W\left(-\frac{\ln x}{x}\right)$ above is a useful identity itself for Lambert W function \begin{equation}\label{eq:funeq4}W\left(-\frac{\ln x}{x}\right)=-\ln x\end{equation} From \eqref{eq:funeq4} we can get some special values of $W$ for example $W(0)=0$ and $W\left(-\frac{1}{e}\right)=-1$. The graphs of $y=x$ and $y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)$ can be seen in Figure 1.
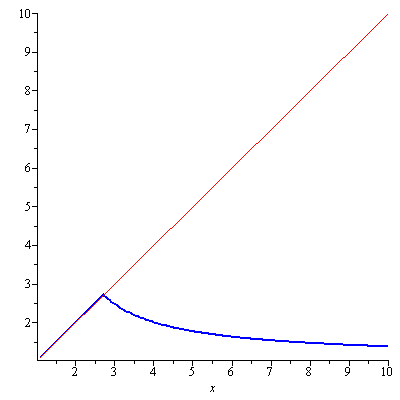
Figure 1. The graphs of y=x (in red) and y=-xW(-ln(x)/x)/ln(x) (in blue)
It appears that $y=x$ and $y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)$ coincide on $(1,e)$. $y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)$ has a kink at $x=e$ and is decreasing on $(e,\infty)$. Differentiating \eqref{eq:funeq} with respect to $x$ results in \begin{equation}\label{eq:funeq5}\frac{1-\ln y}{y^2}\frac{dy}{dx}=\frac{1-\ln x}{x^2}\end{equation} Let $y=f(x)$. Recall $\frac{df^{-1}(x)}{dx}=\frac{1}{\frac{df(x)}{dx}}$. But $f(x)$ is an involution i.e. $f^{-1}=f$ and so $\frac{df(x)}{dx}=\pm 1$. By \eqref{eq:funeq5} with $f(x)$ being an involution, we see that $y=f(x)$ is an increasing function on $(1,e)$ thus $\frac{df(x)}{dx}=1$ and with $f(e)=e$, $f(x)=x$ on $(1,e)$ as we have speculated from Figure 1. $y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)$ parts ways with $y=x$ at $x=e$ and it becomes decreasing on $(e,\infty)$. As for Sam’s last question, first rewrite \eqref{eq:funeq} as $\ln y=y\frac{\ln x}{x}$. Since $y$ is decreasing on $(e,\infty)$ and is bounded below by 1, $\lim_{x\to\infty}y$ must exist, so $\lim_{x\to\infty}\ln y=0$. (This limit is obtained with $\lim_{x\to\infty}\frac{\ln x}{x}=0$.) Since $\lim_{x\to\infty}\ln y=\ln(\lim_{x\to\infty}y)$, $\lim_{x\to\infty}y=1$.
Update:
- I realized that I was sloppy in the definition of $W$. In general $W$ is defined as the collection of the branches of $f(z)=ze^z$ where $z$ is the complex variable $z=x+iy$. $f(z)=ze^z$ is not injective so $W$ is multivalued. I considered the real version which is the inverse of $f(x)=xe^x$ here and I said it is injective. The reason is that I was restricting its domain to $x\geq 0$ though I didn’t mention it. But $f(x)=xe^x$ is in general not injective as seen in Figure 2.
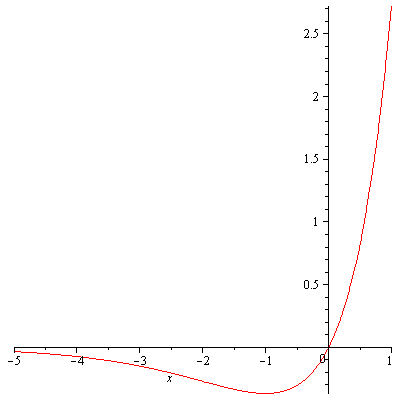
Figure 2. The graph of f(x)=xe^x.
One can also easily show that it is not injective without a graph. $f'(x)=e^x(x+1)$ so $x=-1$ is a critical point. $f'(x)<0$ on $(-\infty,-1)$ i.e. $f(x)$ is decreasing on $(-\infty,-1)$ and $f'(x)>0$ on $(-1,\infty)$ i.e. $f(x)$ is increasing on $(-1,\infty)$. Hence $W$ is still multivalued. The upper branch $W\geq -1$ is denoted $W_0$ and is defined to be the principal branch of $W$ and the lower branch $W\leq -1$ is denoted by $W_{-1}$. Now one can easily see why there is a kink for $y=-\frac{x}{\ln x}W\left(-\frac{\ln x}{x}\right)$ at $x=e$. Because that is where $W$ is failed to be single-valued. In fact, $y=-\frac{x}{\ln x}W_{-1}\left(-\frac{\ln x}{x}\right)$ has no kink as seen in the nice graphics made by Greg Egan here. Also see Figure 3 for the graph of $y=-\frac{x}{\ln x}W_{-1}\left(-\frac{\ln x}{x}\right)$ alone.
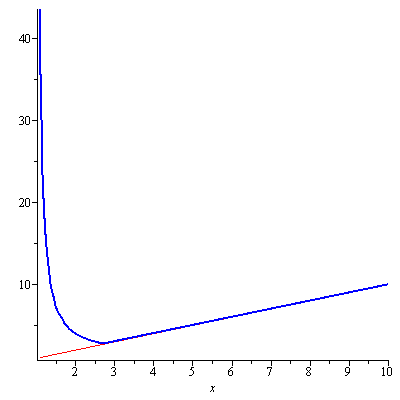
Figure 3. The graphs of y=x (in red) and y=-xW_{-1}(pointed out by Sam-ln(x)/x)/ln(x) (in blue)
By the way, in case you don’t know, Greg is a well-known science fiction writer and his novels have lots of interesting math and physics stuff. For information on his novels visit his website. There is so much interesting stuff to learn about Lambert W function. To learn more about it, for starter, see its Wikipedia entry and also a survey paper on Lambert W function here. Note that one of the authors is Rob Corless. I thought he was just a knowledgeable passerby who threw a hint at others but it turns out he is an expert of Lambert W function.
- By substituting $z_0=ze^z$ in $z=W(ze^z)$ we obtain $z_0=W(z_0)e^{W(z_0)}$ for any complex number $z_0$. This can be used as the defining equation for Lambert $W$ function.
Update:
- After reading Maple information on the command LambertW, I realized that Figure 1 is actually the graph of the principal branch $W_0$.
- The substitutions $u$ and $v$ I used to find the solution of $x^y=y^x$ can be combined into one as pointed out by Sam. Let $v$ be a variable satisfying $y=e^{-v}$. Then \eqref{eq:funeq} turns into $ve^v=-\frac{\ln x}{x}$ as before. In order for $ve^v$ to be injective we require that $-1<v<\infty$ or equivalently $0<y<\frac{1}{e}$.
Update: Sam twitted that the equation $m^n=n^m$ where $m, n$ are integers with $1<m<n$ has only one solution $m=2,n=4$. This can be easily seen from Figure 1. Can we see that without a graph? Yes we can. Since $m\ne n$ and $\frac{\ln m}{m}=\frac{\ln n}{n}$ then, it must be that $m,n\geq 3$ and that $n$ needs to be of the form $k^r$ where both $k,r$ are integers. The first such $n$ is $n=4$ and $\frac{\ln m}{m}=\frac{\ln 4}{4}=\frac{\ln 2}{2}$, thus $m=2$. Since $y$ is decreasing, so is $m$ and hence we see that $(m,n)=(2,4)$ is the only solution to $m^n=n^m$.
