This morning I saw a seemingly random tweet from Sam Walters @SamuelGWalters, a mathematician at the University of Northern British Columbia.

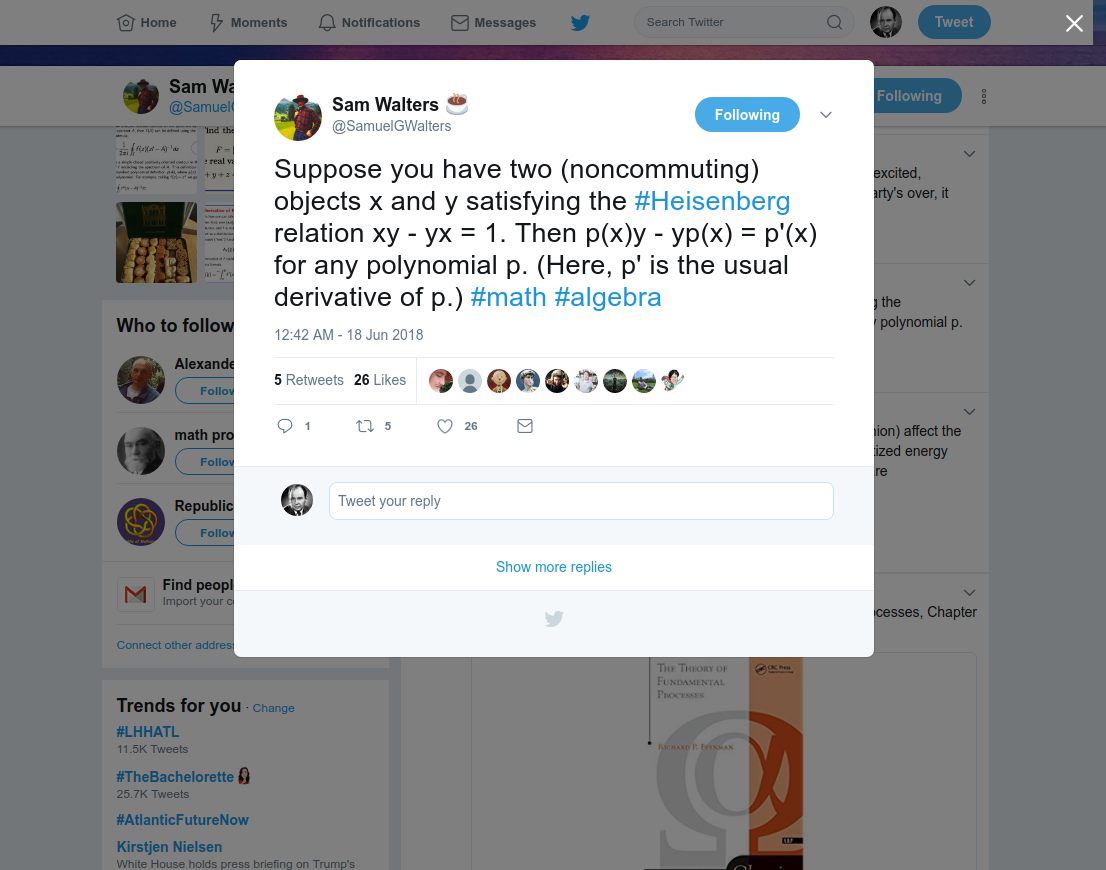
I have no clue as to any motivation behind the tweet but the mathematical statement in it is interesting. It’s proof is pretty easy though. Before we prove the statement, what he referred to as Heisenberg relation (also called Heisenberg commutator) is originated from quantum mechanics where the relation exhibits noncommutativity of the position and the momentum operators $\hat x$ and $\hat p$ as
$$[\hat x,\hat p]=\hat x\hat p-\hat p\hat x=i\hbar$$
in contrast to the classical case ($\hbar\to 0$) where the position and the momentum commute.

Let $\alpha$ and $\beta$ are scalars and $x,y,z$ be vectors (as members of a module or of a Lie algebra depending on the context). Then it is straightforward to show that
$$[\alpha x+\beta y,z]=\alpha[x,z]+\beta[y,z]$$
i.e. the commutator is linear in the first slot. It is also linear in the second slot. Hence the commutator is bilinear. Therefore, it suffices to show that
$$[x^ny,yx^n]=nx^{n-1}$$
for all integers $n\geq 0$. We prove this by induction. It is trivial for $n=0$ and $n=1$. Let $n=2$. Then
\begin{align*}
[x^2y,yx^2]&=x^2y-yx^2\\
&=x^2y-(yx)x\\
&=x^2y-(xy-1)x\\
&=x^2y-xyx+x\\
&=x(xy-yx)+x\\
&=2x
\end{align*}
Now we assume that the statement is true for $n=k$ i.e.
$$[x^ky,yx^k]=kx^{k-1}$$
For $n=k+1$,
\begin{align*}
[x^{k+1}y,yx^{k+1}]&=x^{k+1}y-yx^{k+1}\\
&=x^{k+1}y-(yx)x^k\\
&=x^{k+1}y-(xy-1)x^k\\
&=x^{k+1}y-xyx^k+x^k\\
&=x(x^ky-yx^k)+x^k\\
&=x(kx^{k-1})+x^k\\
&=(k+1)x^k
\end{align*}
This completes the proof.