In this lecture, I am going to introduce you a new idea, which was discovered by Sir Issac Newton and Gottfried Leibiz, to find the slope of a tangent line. This is in fact a quite ingenious idea as you will see. Let a function $y=f(x)$ be given. We want to find the slope of a line tangent to the graph of $y=f(x)$ at a point $x=a$. First consider another point on the $x$-axis that is away from $x=a$. If the distance from $x=a$ to this point is $h$, then the point can be written as $x=a+h$. Let $P(a,f(a))$ and $Q(a+h,f(a+h))$. Then the slope of line segment $\overline{PQ}$ is given by $$\frac{f(a+h)-f(a)}{h}.$$

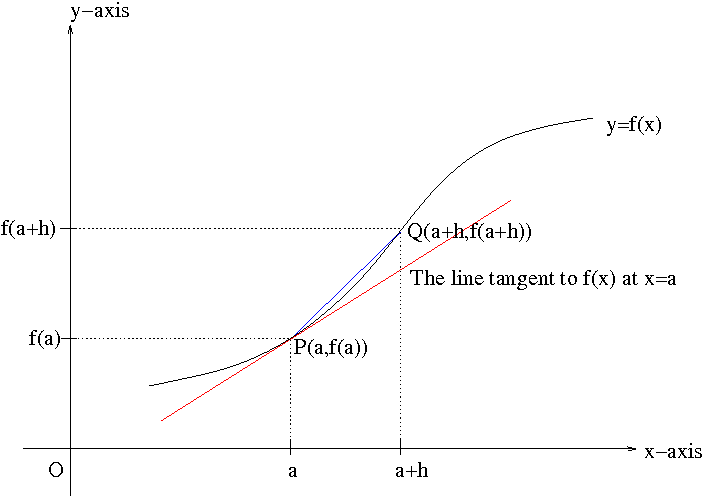
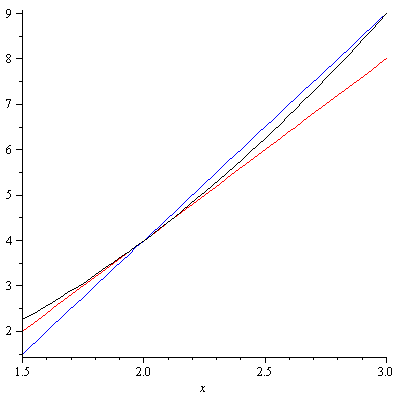
Now we continuously change $h$ so that it gets smaller and smaller close to $0$, consequently the point $a+h$ gets closer to $a$. We want to see how the rate $\frac{f(a+h)-f(a)}{h}$ changes as $h\to 0$. To illustrate the situation better, I will use a specific example, say $f(x)=x^2$ with $a=2$. First we take $h=1$. The following picture shows you the graph of $f(x)=x^2$ (in black), where $1.5\leq x\leq 3$ and the line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ (in blue), and the line tangent to the graph $f(x)=x^2$ at $x=2$ (in red).

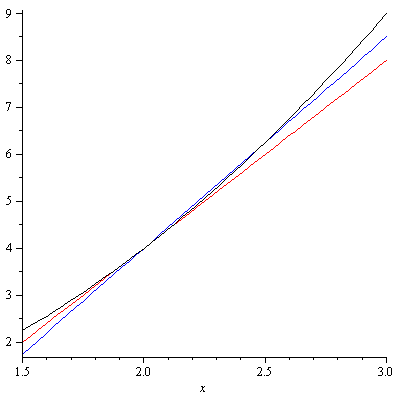
Next we take $h=0.5$. Then the picture becomes

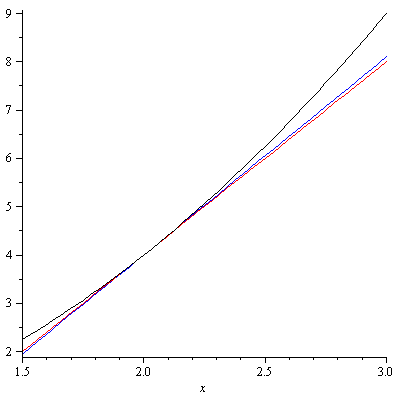
For $h=0.1$, the picture becomes

As one can clearly see, the line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ gets closer to the tangent line as $h$ gets smaller close to $0$. We can still do better. For $h=0.001$, the picture becomes

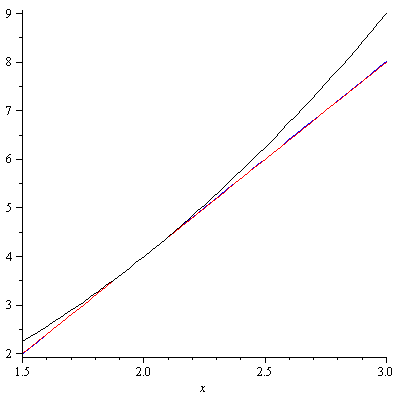
The line through $P(2,4)$ and $Q(2+h,(2+h)^2)$ and the tangent line now appear to be overlapping. From this observation, we can see that the rate $\frac{f(a+h)-f(a)}{h}$ gets closer and closer to the slope of tangent line as $h$ gets smaller and smaller close to $0$. In fact, the slope would be exactly the limit of $\frac{f(a+h)-f(a)}{h}$ as $h$ approaches $0$. Denote the limit by $f'(a)$. Then $$f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}.$$ $f'(a)$ is called the derivative of $f(x)$ at $x=a$. One may wonder why we need another name for the slope of a tangent line. The reason is that as we will see later the slope of a tangent line can mean something else in different contexts. Let $x=a+h$. Then $x\to a$ as $h\to 0$. So $f'(a)$ can be also written as $$f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}.$$ The equation of tangent line to $y=f(x)$ at $x=a$ is then given by $$y-f(a)=f'(a)(x-a).$$

Example. Find the equation of tangent line to the graph of $f(x)=x^2$ at $x=2$.

Solution. First we need to find $f'(2)$, i.e. the slop of the tangent line. \begin{eqnarray*}f'(2)&=&\lim_{h\to 0}\frac{f(2+h)-f(2)}{h}\\&=&\lim_{h\to 0}\frac{(2+h)^2-4}{h}\\&=&\lim_{h\to 0}\frac{4+4h+h^2-4}{h}\\&=&\lim_{h\to 0}(4+h)\\&=&4.\end{eqnarray*}

Of course, we can also use the alternative definition of $f'(a)$ to calculate the slope:\begin{eqnarray*}f'(2)&=&\lim_{x\to 2}\frac{f(x)-f(2)}{x-2}\\&=&\lim_{x\to 2}\frac{x^2-4}{x-2}\\&=&\lim_{x\to 2}\frac{(x+2)(x-2)}{x-2}\\&=&\lim_{x\to 2}(x+2)\\&=&4.\end{eqnarray*}

The equation of tangent line is then $y-4=4(x-2)$ or $y=4x-4$.

Remark. One may wonder which definition of $f'(a)$ to use. I would say that is the matter of a personal taste. For a polynomial function, one notable difference between the two definitions is that if you use the first definition, you will end up expanding a polynomial, while you will have to factorize a polynomial with the second definition. Since the expansion of a polynomial is easier than the factorization, you may want to use the first definition if you are not confident with factorizing polynomials.

Example. Find the equation of tangent line to the graph of $f(x)=x^5$ at $x=1$.

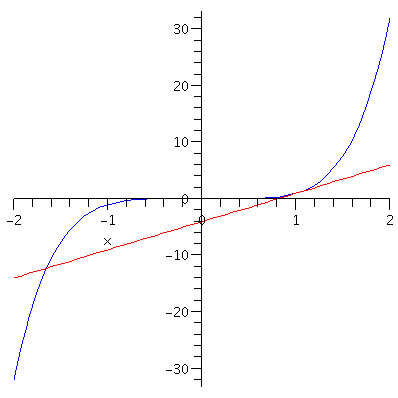
Solution. As we discussed in the previous lecture, this is an extremely difficult problem to solve by using only algebra if not impossible. But surprise! With the new method, this is more or less a piece of cake. First we calculate the slope $f'(1)$. \begin{eqnarray*}f'(1)&=&\lim_{h\to 0}\frac{(1+h)^5-1}{h}\\&=&\lim_{h\to 0}\frac{(1+h)^5-1}{h}\\&=&\lim_{h\to 0}\frac{1+5h+10h^2+10h^3+5h^4+h^5-1}{h}\\&=&\lim_{h\to 0}(5+10h+10h^2+5h^3+h^4)\\&=&5.\end{eqnarray*} Or by the second definition, \begin{eqnarray*}f'(1)&=&\lim_{x\to 1}\frac{f(x)-f(1)}{x-1}\\&=&\lim_{x\to 1}\frac{x^5-1}{x-1}\\&=&\lim_{x\to 1}\frac{(x-1)(x^4+x^3+x^2+x+1)}{x-1}\\&=&\lim_{x\to 1}(x^4+x^3+x^2+x+1)\\&=&5.\end{eqnarray*}Therefore the equation of the tangent line is given by $y-1=5(x-1)$ or $y=5x-4$. The following picture shows the graph of $y=x^5$ (in blue) and the graph of tangent line $y=5x-4$.