Let us consider a simple geometry problem. Given a curve $y=f(x)$, we want to find a line tangent to the graph of $y=f(x)$ at $x=a$ (meaning the line meets the graph of $y=f(x)$ exactly at a point $(a,f(a))$ on a small interval containing $x=a$.

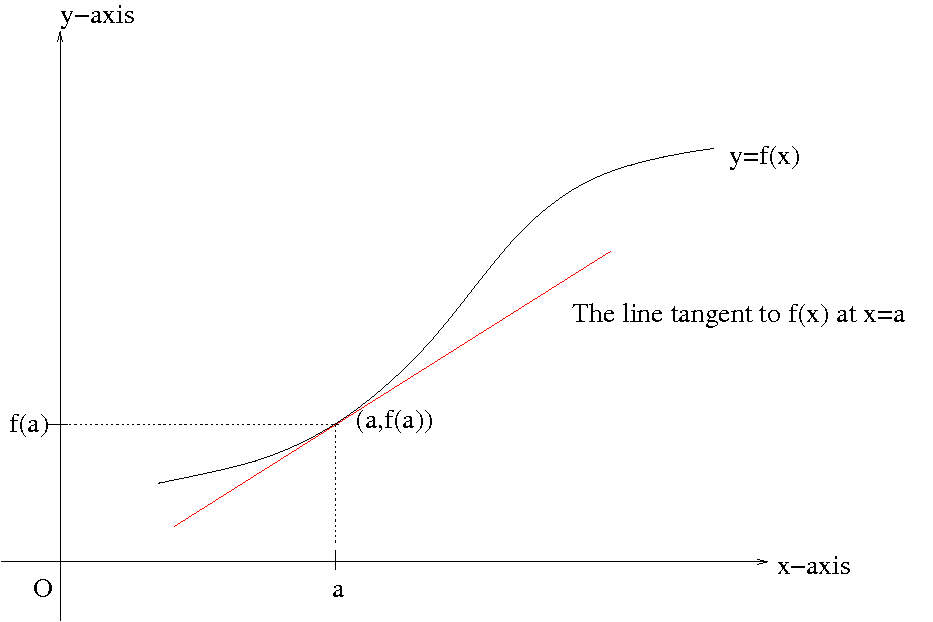
One may wonder at this point why finding a tangent line is a big deal. Well, it is in fact a pretty big deal besides mathematicians’ purely intellectual curiosities. There is a reason why Sir Issac Newton had to invent calculus of which crucial notion is the slope of a tangent line. It is still too early to talk about why it is important or useful. We will get there when we are ready.

We attempt to tackle the problem with an example first. Here is an example we want to consider

Example. Find the equation of a line tangent to the graph of $y=x^2$ at $x=2$.

Solution. To find the equation of a line, we need two ingredients: slope and $y$-intercept or slope and a point. We already know a point. We know that the line must pass through $(2,4)$. So all we need to find is its slope $m$. From algebra, we know that the equation of a line passing through $(2,4)$ with slope $m$ is given by $y-4=m(x-2)$ or $y=mx-2m+4$. Since $y=x^2$ and $y=mx-2m+4$ meet exactly at one point, the quadratic equation $x^2=mx-2m+4$ or $x^2-mx+2m-4=0$ must have exactly one solution. We have learned from the theory of quadratic equations that in that case the discriminant $D=b^2-4ac$ must be equal to $0$. That is, in our case $$D=m^2-4(2m-4)=m^2-8m+16=(m-4)^2=0.$$ Hence we determine that $m=4$ and the equation of the tangent line is $y=4x-4$.

So we see that finding the slope of a tangent line is not that difficult and that it does not require any new mathematics, or does it? Remember that we have not yet tackled our problem in general context. Before we get more ambitious, consider another example with a more complicated function, say $y=x^5$. Let us say that we want to find the line tangent to the graph of $y=x^5$ at $x=1$. Then the equation of the tangent line would be $y=mx-m+1$. In order for $y=x^5$ and the line $y=mx-m+1$ to meet exactly at one point, the quintic equation $x^5-mx+m-1=0$ must have exactly one solution. Our problem here is that we have no algebraic means, such as quadratic formula or discriminant, to use to determine the value of $m$. We are stuck here and there is no hope of tackling our simple geometry problem using only algebra. That is the reason why we have to cleverly devise a new way to tackle the problem. This is where we enter the realm of Calculus. The new idea to tackle the problem is not really new and it was already used by the ancient Greeks. And the world had to wait until it was rediscovered independently by Sir Issac Newton and by Gottfried Leibniz. I do not know if any of them actually knew about the ancient Greek idea.