The harmonic motion we discussed here is not physically realistic because it does not take damping due to friction into account. In this note, we discuss damped harmonic motion which is physically more realistic. If $x$ is the displacement from the equilibrium position, then the restoring force exerted by a spring is $-kx$ and the retarding force is $-cv$ (friction is proportional to the velocity $v$). Consequently we have the equation $$F=-kx-cv=-kx-c\dot{x}$$ or equivalently the second-order linear equation \begin{equation}\label{eq:damped}m\ddot{x}+c\dot{x}+kx=0\end{equation} To solve the equation \eqref{eq:damped} we still attempt to use the trial solution $x=e^{qt}$. As a result we obtain \begin{equation}\label{eq:chareq}mq^2+cq+k=0\end{equation} \eqref{eq:chareq} is called the auxiliary equation or the characteristic equation. Its solution is given by $$q=\frac{-c\pm\sqrt{c^2-4mk}}{2m}$$ There are three physically distinct cases:

1. $c^2>4mk$: overdamping
2. $c^2=4mk$: critically damping
3. $c^2<4mk$: underdamping

Case 1. Let $-\gamma_1<0$ and $-\gamma_2<0$ be two real values of $q$. Then the general solution (we will discuss, using linear algebra, why this is indeed the general solution later) is $$x=A_1e^{-\gamma_1 t}+A_2e^{-\gamma_2 t}$$ The motion is nonoscillatory and the displacement $x$ decays to 0 in an exponential matter.

Example. The second-order linear differential equation $\ddot{x}+3\dot{x}+2x=0$ has the general solution $$x(t)=A_1e^{-2t}+A_2e^{-t}$$

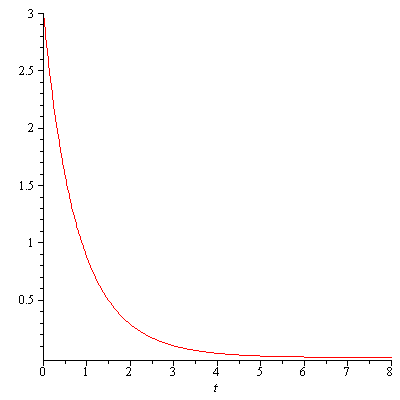
x(t)=exp(-2t)+2exp(-t), t=0..8

Case 2. $q$ has one real value $q=-\gamma$ where $\gamma=\frac{c}{2m}$. The equation \eqref{eq:damped} can be written as \begin{equation}\label{eq:criticdamped}\left(\frac{d}{dt}+\gamma\right)^2x=\left(\frac{d}{dt}+\gamma\right)\left(\frac{d}{dt}+\gamma\right)x=0\end{equation} Let $u=\frac{d}{dt}+\gamma$. Then \eqref{eq:criticdamped} reduces to  a first-order differential equation $$\left(\frac{d}{dt}+\gamma\right)u=\frac{du}{dt}+\gamma u=0$$ which is separable. It’s solution is $u=A_1e^{-\gamma t}$. Now we have a first-order linear differential equation $$\frac{dx}{dt}+\gamma x=A_1e^{-\gamma t}$$ whose solution is given by $$x(t)=e^{-\gamma t}(A_1 t+A_2)$$

Example. The second-order linear differential equation $$\ddot{x}+2\dot{x}+x=0$$ has the general solution $$x(t)=e^{-t}(A_1t+A_2)$$

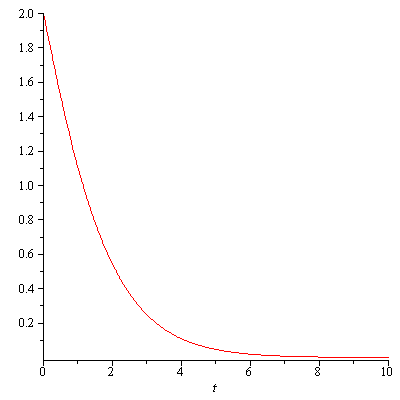
x(t)=exp(-t)(t+2), t=0..10

This also represents a nonoscillatory motion and the displacement $x$ decays to zero asymptotically. Critical damping produces an optimal return to the equilibrium position, so it is used, for example, for galvanometer suspensions.

Case 3. Suppose that $c$ is small enough so that $c^2-4mk<0$. In this case, $q$ are two complex numbers $-\gamma\pm i\omega_1$ where $\gamma=\frac{c}{2m}$, $\omega_1=\sqrt{\frac{k}{m}-\frac{c^2}{4m^2}}=\sqrt{\omega_0^2-\gamma^2}$. So $e^{(-\gamma+i\omega_1)t}$, $e^{(-\gamma-i\omega_1)t}$ are solutions of \eqref{eq:damped}. Due to the linearity of \eqref{eq:damped}, the real part $e^{-\gamma t}\cos\omega_1 t$and the imaginary part $e^{-\gamma t}\sin\omega_1 t$ of $e^{(-\gamma+i\omega_1)t}$ are also solutions of \eqref{eq:damped}. Hence, $$x(t)=ae^{-\gamma t}\cos\omega_1 t+be^{-\gamma t}\sin\omega_1 t$$ is the general solution. This can be written as $$x(t)=Ae^{-\gamma t}\cos(\omega_1 t-\theta_0)$$ where $A=\sqrt{a^2+b^2}$ and $\theta_0=\tan^{-1}\left(\frac{b}{a}\right)$. Note that the angular frequency (or natural frequency) $\omega_1$ is smaller than that of undamped harmonic oscillator $\omega_0$. $$\omega_1=\sqrt{\omega_0^2-\gamma^2}=\omega_0\sqrt{1-\left(\frac{\gamma}{\omega_0}\right)^2}$$ If $\frac{\gamma}{\omega_0}<1$ then $\sqrt{1-\left(\frac{\gamma}{\omega_0}\right)^2}\approx 1-\frac{1}{2}\frac{\gamma^2}{\omega_0^2}$. So $$\omega_1\approx \omega_0-\frac{\gamma^2}{2\omega_0}$$

Example. Let $m=1$, $c=4$ and $k=404$. Then the resulting equation of damped harmonic oscillator is $$\ddot{x}+4\dot{x}+404=0$$ Let us solve this equation with $x(0)=1$ and $\dot{x}(0)=0$. The characteristic equation $$q^2+4q+404=0$$ has two complex solutions $q=-2\pm 20i$. Thus $$x(t)=ae^{-2t}\cos(20t)+be^{-2t}\sin(20t)$$ $x(0)=1$ results in $a=1$. To determine $b$ we need $\dot{x}$. $$\dot{x}=-2e^{-2t}\cos(20t)-20e^{-2t}\sin(20t)-2be^{-2t}\sin(20t)+20be^{-2t}\cos(20t)$$ The initial condition $\dot{x}(0)=0$ results in $b=\frac{1}{10}$. Hence $x(t)$ is given by $$x(t)=e^{-2t}\cos(20t)+\frac{1}{10}e^{-2t}\sin(20t)$$ Since $A=\sqrt{a^2+b^2}=\frac{\sqrt{101}}{10}$ and $\theta_0=\tan^{-1}\left(\frac{b}{a}\right)=\tan^{-1}\left(\frac{1}{10}\right)\approx 0.099669$, $x(t)$ also can be written as $$x(t)=\frac{\sqrt{101}}{10}e^{-2t}\cos(20t-0.099669)$$

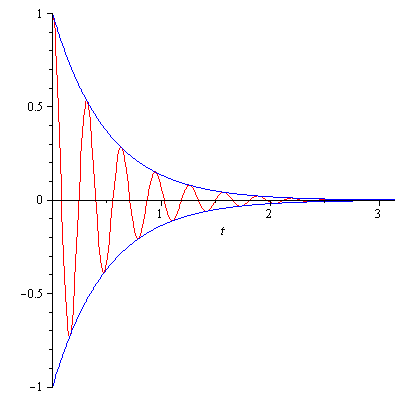
x(t)=1.00499exp(-2t)cos(20t-0.099669), t=0..pi

Differentiate the total energy $$E=\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2$$ with respect to $t$. \begin{align*}\frac{dE}{dt}&=m\ddot{x}\dot{x}+k\dot{x}x\\&=(m\ddot{x}+kx)\dot{x}\\&=(-c\dot{x})\dot{x}\\&=-c(\dot{x})^2<0\end{align*} This is the rate at which energy is dissipated into heat by friction.