A force exerted by an elastic cord or by a spring obeys Hooke’s law $F=-kx$ where $x$ is the displacement of the equilibrium position.

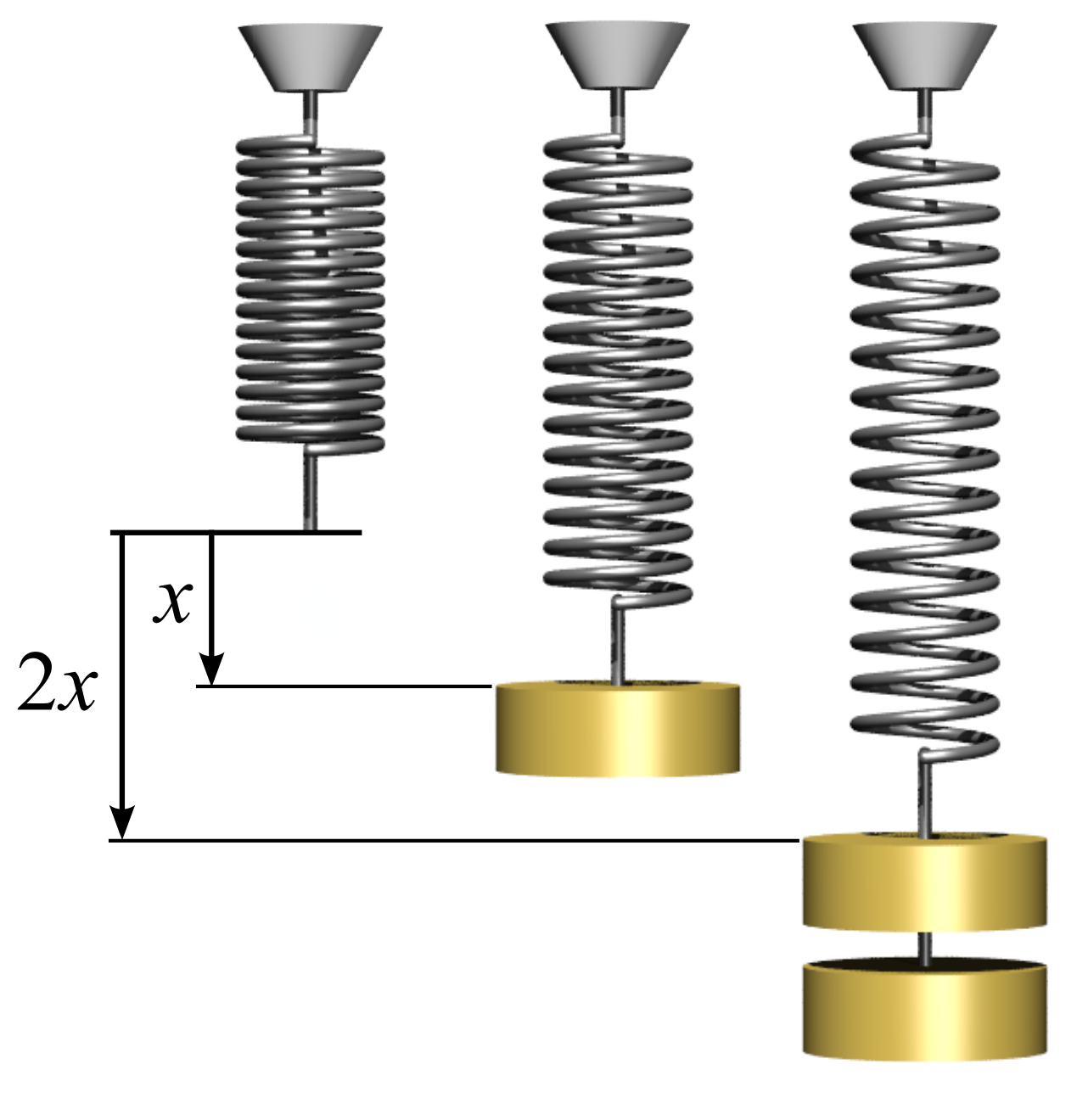
Credit: This picture was taken from a Wikipedia page at https://en.wikipedia.org/wiki/File:Hookes-law-springs.png

From Newton’s second law of motion we have $F=ma=m\ddot{x}$, so we obtain the second order linear differential equation \begin{equation}\label{eq:undamped}m\ddot{x}+kx=0\end{equation} Solving \eqref{eq:undamped} for $\ddot{x}$ we obtain $\ddot{x}=-\frac{k}{m}x\sim -x$. For a trial solution, $x=e^{qt}$ is a candidate. To see if this trial solution works, plug it back into \eqref{eq:undamped}. $$m\ddot{x}+kx=mq^2e^{qt}+ke^{qt}=0$$ i.e. \begin{equation}\label{eq:auxeq}mq^2+k=0\end{equation} whose solutions are $$q=\pm i\sqrt{\frac{k}{m}}=\pm i\omega_0$$ where $\omega_0=\sqrt{\frac{k}{m}}$. The equation \eqref{eq:auxeq} is called the auxiliary equation or the characteristic equation. So, $x_1=e^{i\omega_0 t}$ and $x_2=e^{-i\omega_0 t}$ are solutions of \eqref{eq:undamped}. It can be easily shown that their linear combination \begin{equation}\label{eq:undamped2}x=A_1e^{i\omega_0 t}+A_2e^{-i\omega_0 t}\end{equation} is also a solution of \eqref{eq:undamped}. \eqref{eq:undamped2} is a complex solution so it is not suitable for the physical analysis of a motion governed by \eqref{eq:undamped}. What we need is a real solution. It turns out that the real part and the imaginary part of $e^{i\omega_0 t}$ also, respectively, satisfy \eqref{eq:undamped}. This is due to the linearity of \eqref{eq:undamped}. Hence, an alternative form of the solution which is real is \begin{equation}\label{eq:undamped3}x=a\cos\omega_0 t+b\sin\omega_0 t\end{equation} Using a trigonometric identity \eqref{eq:undamped3} can be written as \begin{equation}\label{eq:undamped4}x=\sqrt{a^2+b^2}\cos(\omega_0 t-\theta_0)\end{equation} where $\theta_0=\tan^{-1}\frac{b}{a}$ or as \begin{equation}\label{eq:unddamped4a}x=\sqrt{a^2+b^2}\sin(\omega_0 t+\phi_0)\end{equation} where $\phi_0=\tan^{-1}\frac{a}{b}$. The angles $\theta_0$ and $\phi_0$ are called the phase.

Some Terminologies

The equation \eqref{eq:undamped} is called the differential equation of the harmonic oscillator. $\sqrt{a^2+b^2}$ is the amplitude (the maximum value of $x$) The period $T_0$ of the oscillation is the time required for one complete cycle. $$T_0=\frac{2\pi}{\omega_0}=2\pi\sqrt{\frac{m}{k}}$$ The linear frequency of oscillation $f_0$ is the number of cycles in unit time. $$f_0=\frac{1}{T_0}=\frac{\omega_0}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$$ $\omega_0=2\pi f_0$ is called the angular frequency and is also called the natural frequency.

Example. Suppose that a mass weighing 10 lb stretches a spring 2 in. If the mass is displaced an additional 2 in and is then set in motion with an initial upward velocity of 1 ft/s, determine the position of the mass at any later time. Also determine the period, amplitude, and phase of the motion.

Solution. $k=10\mathrm{lb}/2\mathrm{in}=60\mathrm{lb}/\mathrm{ft}$ and $m=\mathrm{weight}/g=10\mathrm{lb}/32\mathrm{ft}/\mathrm{s}^2$. Thus $$m\ddot{x}+kx=\frac{10}{32}\ddot{x}+60x=0$$ i.e. $$\ddot{x}+192x=0$$ The auxiliary equation is $q^2+192=0$ and $q=\pm i8\sqrt{3}$. The solution $x(t)$ is then given by $$x(t)=a\cos(8\sqrt{3}t)+b\sin(8\sqrt{3}t)$$ From the initial conditions $x(0)=\frac{1}{6}$ ft and $\dot{x}(0)=-1$ ft/s, we find $a=\frac{1}{6}$ and $b=-\frac{1}{8\sqrt{3}}$. The natural frequency is $\omega_0=8\sqrt{3}\approx 13.856$ rad/s. The period is $T_0=\frac{2\pi}{\omega_0}=\frac{2\pi}{8\sqrt{3}}\approx 0.453$ sec. The amplitude is $\sqrt{a^2+b^2}=\sqrt{\frac{19}{576}}\approx 0.182$ ft. The phase is $\theta_0=\tan^{-1}\left(\frac{b}{a}\right)=-\frac{\sqrt{3}}{4}\approx -0.408645$ rad. Therefore, $x(t)$ can be written as $$x(t)=0.182\cos(13.856t+0.40864)$$ Figure 1 shows a complete cycle.

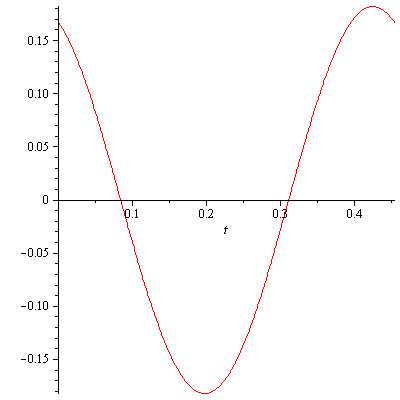
Figure 1. A complete cycle of x(t)=0.182cos(13.856t+0.40864)

Figure 2. shows an animation of $x(t)$.

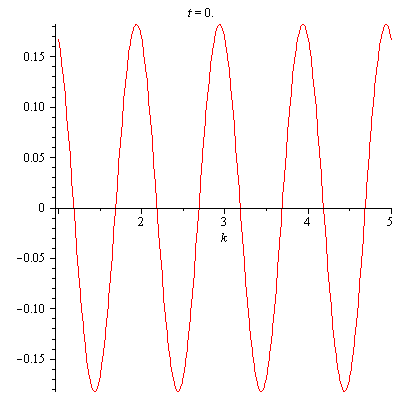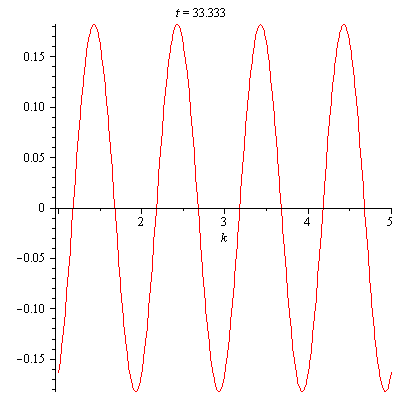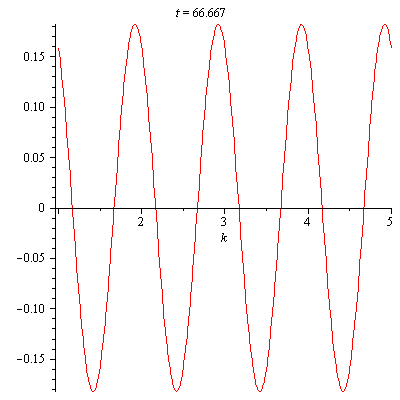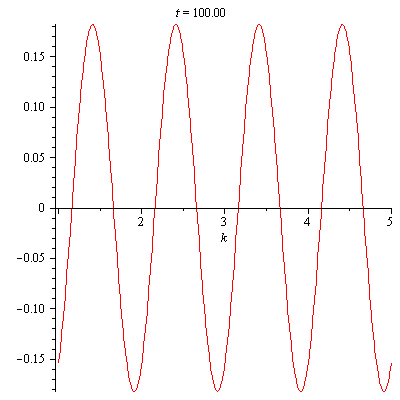
Figure 2. An animation of x(t)=0.182cos(13.856t+6.283185308k+0.40864) with k=1..5, t=1..100, and FPS=10

The Conservation of Total Energy

Let us calculate the work done by an external force $F_{\mathrm{ext}}$ in moving the mass from the equilibrium position ($x=0$) to some position $x$. $F_{\mathrm{ext}}=-F=kx$ and $$W=\int F_{\mathrm{ext}} dx=\int_0^x kx dx=\frac{1}{2}kx^2$$ The work $W$ is stored in the spring as potential energy $V(x)=W=\frac{1}{2}kx^2$. The potential energy $V(x)$ for a force $F(x)$ is defined by \begin{equation}\label{eq:conservative}F=-\frac{dV}{dx}\end{equation} In our case, $F=-\frac{dV}{dx}=-kx$. For any force $F$ satisfying \eqref{eq:conservative}, the total energy $$E=T+V,$$ the sum of the kinetic energy $T=\frac{1}{2}m\dot{x}^2$ and the potential energy $V$, is  constant. For this reason, a force satisfying \eqref{eq:conservative} is called a conservative force.  Since $$\ddot{x}=\frac{d\dot{x}}{dt}=\frac{d\dot{x}}{dx}\frac{dx}{dt}=v\frac{dv}{dx},$$ $$F(x)=m\ddot{x}=mv\frac{dv}{dx}=\frac{1}{2}m\frac{dv^2}{dx}=\frac{dT}{dx}$$ The work done on the particle by impress force $F(x)$ is $$\int F(x)dx=\int dT=\frac{1}{2}m\dot{x}^2+C_1$$ where $C_1$ is a constant. On the other hand, from \eqref{eq:conservative} we also have $$\int F(x)dx=-\int dV=-V(x)+C_2$$ where $C_2$ is a constant. Therefore, $$T+V=\frac{1}{2}m\dot{x}^2+V(x)=E$$ is a constant. In our case the conservation of total energy $E$ \begin{equation}\label{eq:totalenergy}E=\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2\end{equation} can be more directly shown. Differentiating the total energy \eqref{eq:totalenergy} with respect to $t$ \begin{align*}\frac{dE}{dt}&=m\ddot{x}\dot{x}+kx\dot{x}\\&=(m\ddot{x}+kx)\dot{x}\\&=0\end{align*} So the restoring force $F=-kx$ for an undamped harmonic motion is conservative.

The solution \eqref{eq:undamped4} can be also obtained by considering energy. Solving \eqref{eq:totalenergy} for $\dot{x}$ \begin{equation}\label{eq:velocityundamped}\dot{x}=\pm\sqrt{\frac{2E-kx^2}{m}}\end{equation} This is a separable equation. For $\dot{x}=\sqrt{\frac{2E-kx^2}{m}}$ it’s solution is  $$x=\sqrt{\frac{2E}{k}}\sin\left(\sqrt{\frac{k}{m}}t+\phi_0\right)$$ and for $\dot{x}=-\sqrt{\frac{2E-kx^2}{m}}$, it’s solution is $$x=\sqrt{\frac{2E}{k}}\cos\left(\sqrt{\frac{k}{m}}t-\theta_0\right)$$ So the amplitude is $A=\sqrt{\frac{2E}{k}}$ and the angular frequency is $\omega_0=\sqrt{\frac{k}{m}}$. In order for \eqref{eq:velocityundamped} to make sense $\frac{2E-kx^2}{m}\geq 0$ i.e. the total energy is greater than or equal to the potential energy $V(x)=\frac{1}{2}kx^2$. This means that the particle is confined to the region $-\sqrt{\frac{2E}{k}}\leq x\leq\sqrt{\frac{2E}{k}}$. Also the speed becomes zero when $V(x)=E$. This means that the particle must come to rest and reverse its motion at $x=\pm\sqrt{\frac{2E}{k}}$. The points $x=\pm\sqrt{\frac{2E}{k}}$ are called the turning points of the motion. The maximum value of $\dot{x}$ occurs at $x=0$. $v_{\max}=\frac{k}{m}A=\omega_0A$ and $E=\frac{1}{2}mv_{\max}^2=\frac{1}{2}kA^2$.