The definition of a limit we previously discussed here is intuitive and qualitative rather than quantitative. It may be helpful for us to conceptually understand the notion of a limit, but it is useless when you try to prove some fundamental properties of limits, for instance the properties described in the following theorem.

Theorem. Suppose that \(c\) is a constant and the limits \[\lim_{x\to a}f(x)\ {\rm and}\ \lim_{x\to a}g(x)\] exist. Then the following properties hold:

1. \(\displaystyle\lim_{x\to a}\{f(x)+g(x)\}=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)\)
2. \(\displaystyle\lim_{x\to a}cf(x)=c\lim_{x\to a}f(x)\)
3. \(\displaystyle\lim_{x\to a}f(x)g(x)=\lim_{x\to a}f(x)\cdot\lim_{x\to a}g(x)\)
4. \(\displaystyle\lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}\) provided \(\displaystyle\lim_{x\to a}g(x)\ne 0\)

For a long time, mathematicians have believed that the above properties were true and have used them without having been able to prove them. A limit is a mathematical quantity and in order to deal with a mathematical quantity, one needs to have a quantitative definition. And a quantitative definition must consist of quantities that are finite. Finally a French mathematician Augustin-Louis Cauchy came up with such a definition.

Definition. [\(\epsilon-\delta\) Argument] A function \(f(x)\) is said to approach a value \(A\) as \(x\) approaches \(a\), if for any given positive number \(\epsilon>0\) (no matter how small it is) there exists a positive number \(\delta>0\) such that \[|f(x)-A|<\epsilon\] is true for every \(x\) that satisfies the inequality \[0<|x-a|<\delta.\]

The following picture also shows you why this definition makes sense.

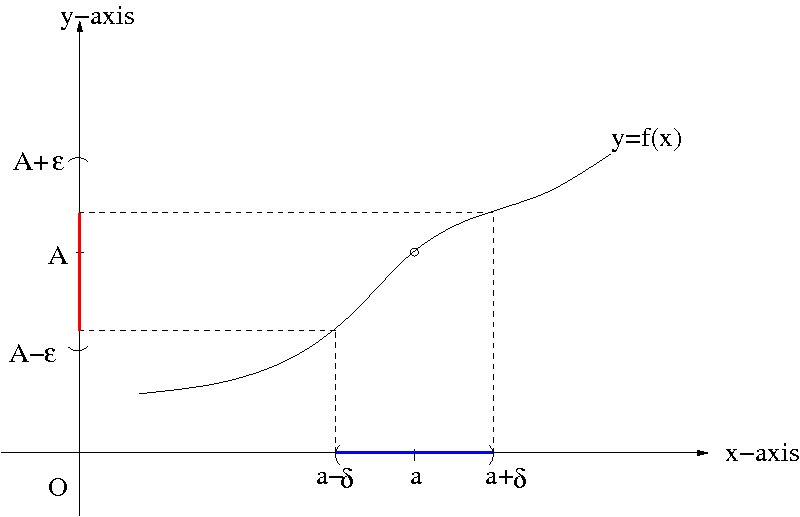
The limit of f(x) is A when x approaches a.

Example. Prove that \(\displaystyle\lim_{x\to 2}(5x-2)=8\).

Solution: Let \(\epsilon>0\) be given. Then we want to show that there exists \(\delta>0\) such that \[|(5x-2)-8|=|5x-10|<\epsilon\] is satisfied, whenever \(x\) is in the domain \[0<|x-2|<\delta.\] Now divide the inequality \(|5x-10|<\epsilon\) by \(5\). Then we obtain \[|x-2|<\frac{\epsilon}{5}.\] Hence, \(\delta=\frac{\epsilon}{5}\)is an adequate choice for \(\delta\) and the proof is complete.

If \(\epsilon=0.005\), the proceeding result tells us that the function \(5x-2\) will lie in the range \(7.995<5x-2<8.005\) whenever the domain of \(x\) is \(1.999<x<2.001\).

Example. In order to see why the above definition does not work for non-existing limits, let us recall the second example from my previous posting: \[f(x)=\left\{\begin{array}{ccc}x-1 & {\rm if} & x<2\\(x-2)^2+3 & {\rm if} & x\geq 2.\end{array}\right.\] Let us show that the left-hand limit \(1\) of \(f(x)\) at \(x=2\) cannot be a limit of \(f(x)\) when \(x\) approaches \(2\). Let \(\epsilon=1\). Then no matter how small \(\delta>0\) one chooses there is a number \(2<x_0<2+\delta\) and \(f(x_0)>3\). That is, \(f(x_0)\) does not satisfy the inequality \(0<f(x)<2\). Hence, \(2\) cannot be a limit. Similarly, one can show that the right-hand limit \(3\) of \(f(x)\) at \(x=1\) cannot be a limit either.

In order to see how the Cauchy’s definition of a limit can be used to prove some fundamental properties of limits, we prove the first property of the above theorem: If \[\lim_{x\to a}f(x)=A\ {\rm and}\ \lim_{x\to a}g(x)=B\] then \[\lim_{x\to a}\{f(x)+g(x)\}=A+B.\]

Proof. Let \(\epsilon>0\) be given. Since \(\displaystyle\lim_{x\to a}f(x)=A\) and \(\displaystyle\lim_{x\to a}g(x)=B\), there exist \(\delta_1>0\) and \(\delta_2>0\) such that \[|f(x)-A|<\frac{\epsilon}{2},\] whenever \(0<|x-a|<\delta_1\) and such that \[|g(x)-B|<\frac{\epsilon}{2},\] whenever \(0<|x-a|<\delta_2\). Choose \(\delta=\min(\delta_1,\delta_2)\), i.e. we choose \(\delta\) to be the smaller of \(\delta_1\) and \(\delta_2\). Now if \(x\) satisfies the inequality \[0<|x-a|<\delta\] then \[|f(x)+g(x)-(A+B)|=|f(x)-A+g(x)-B|\leq |f(x)-A|+|g(x)-B|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon.\] This completes the proof.

The rest of the properties in the above theorem can be proved in a similar manner. I stumbled upon the Cauchy’s definition of a limit back when I was a high school senior. Once I understood what it means I was so amazed by its beauty. After I proved all the properties listed in the above theorem, I nearly experienced Nirvana and Enlightenment or more precisely speaking I tasted very slightly what they would be like. It was a long time ago, but I still remember the joy and the excitement from that little experience. It was an awakening moment for me that opened my eyes to the beauty of the Nature and the Universe. I can’t say I am spiritual but that experience surely led me to mathematics. Won’t you try to discover and experience some of it too?