Let $f(x)$ and $g(x)$ be differentiable functions. Then the product rule
$$(f(x)g(x))’=f'(x)g(x)+f(x)g'(x)$$
leads to the integration
\begin{equation}
\label{eq:intpart}
\int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx.
\end{equation}
The formula \eqref{eq:intpart} is called integration by parts. If we set $u=f(x)$ and $v=g(x)$, then \eqref{eq:intpart} can be also written as
\begin{equation}
\label{eq:intpart2}
\int udv=uv-\int vdu.
\end{equation}

Example. Evaluate $\int x\cos xdx$.

Solution. Let $u=x$ and $dv=\cos xdx$. Then $du=dx$ and $v=\sin x$. So,
\begin{align*}
\int x\cos xdx&=x\sin x-\int\sin xdx\\
&=x\sin x+\cos x+C,
\end{align*}
where $C$ is a constant.

Example. Evaluate $\int\ln xdx$.

Solution. Let $u=\ln x$ and $dv=dx$. Then $du=\frac{1}{x}dx$ and $v=x$. So,
\begin{align*}
\int\ln xdx&=x\ln x-\int x\cdot\frac{1}{x}dx\\
&=x\ln x-x+C,
\end{align*}
where $C$ is a constant.

Often it is required to apply integration by parts more than once to evaluate a given integral. In that case, it is convenient to use tabular integral (which is equivalent to integration by parts) as shown in the following example.

Example. Evaluate $\int x^2e^xdx$

Solution. In the following table, the first column represents $x^2$ and its derivatives, and the second column represents $e^x$ and its integrals.
$$\begin{array}{ccc}
x^2 & & e^x\\
&\stackrel{+}{\searrow}&\\
2x & & e^x\\
&\stackrel{-}{\searrow}&\\
2 & & e^x\\
&\stackrel{+}{\searrow}&\\
0 & & e^x.
\end{array}$$
This table shows the repeated application of integration by parts. Following the table, the final answer is given by
$$\int x^2e^xdx=x^2e^x-2xe^x+2e^x+C,$$
where $C$ is a constant.

In order to understand why this works and why this is equivalent to integration by parts, assume that we are to evaluate the integral $\int fgdx$. Let $u=f$ and $dv=gdx$. Then by \eqref{eq:intpart2} $$\int fgdx=f\int gdx-\int f’\left(\int gdx\right)dx$$ If $\int f’\left(\int gdx\right)dx$ requires integration by parts, we would have $$\int fgdx=f\int gdx-f’\int\left(\int gdx\right)dx+\int f^{\prime\prime}\left(\int\left(\int gdx\right)dx\right)dx$$ If $\int f^{\prime\prime}\left(\int\left(\int gdx\right)dx\right)dx$ still requires integration by parts, we would have \begin{align*}\int fgdx&=f\int gdx-f’\int\left(\int gdx\right)dx+f^{\prime\prime}\int\left(\int\left(\int gdx\right)dx\right)dx\\&-\int f^{\prime\prime\prime}\left(\int\left(\int\left(\int gdx\right)dx\right)\right)dx\end{align*} This illustrates tabular integral and the process continues until the last integral no longer requires integration by parts. Sometimes the last integral becomes the same type of integral as the one in the LHS up to a constant. When that happens the last integral can be combined with the one in the LHS.

Example. Evaluate $\int x^3\sin xdx$.

Solution. In the following table, the first column represents $x^3$ and its derivatives, and the second column represents $\sin x$ and its integrals.
$$\begin{array}{ccc}
x^3 & & \sin x\\
&\stackrel{+}{\searrow}&\\
3x^2 & & -\cos x\\
&\stackrel{-}{\searrow}&\\
6x & & -\sin x\\
&\stackrel{+}{\searrow}&\\
6 & & \cos x\\
&\stackrel{-}{\searrow}&\\
0 & & \sin x.
\end{array}$$
Following the table, the final answer is given by
$$\int x^3\sin xdx=-x^3\cos x+3x^2\sin x+6x\cos x-6\sin x+C,$$
where $C$ is a constant.

Example. Evaluate $\int e^x\cos xdx$.

Solution. In the following table, the first column represents $e^x$ and its derivatives, and the second column represents $\cos x$ and its integrals.
$$\begin{array}{ccc}
e^x & & \cos x\\
&\stackrel{+}{\searrow}&\\
e^x & & \sin x\\
&\stackrel{-}{\searrow}&\\
e^x & & -\cos x.
\end{array}$$
Now, this is different from the previous two examples. While the first column repeats the same function $e^x$, the functions second column changes from $\cos x$ to $\sin x$ and to $\cos x$ again up to sign. In this case, we stop there and write the answer as we have done in the previous two examples and add to it $\int e^x(-\cos x)dx$. Notice that the integrand is the product of functions in the last row and this is the last integral we obtain from a multiple applications of integration by parts, which becomes the same type of integral as the one you began with. Hence,
$$\int e^x\cos xdx=e^x\sin x+e^x\cos x-\int e^x\cos xdx.$$
For now we do not worry about the constant of integration. Solving this for $\int e^x\cos xdx$, we obtain the final answer
$$\int e^x\cos xdx=\frac{1}{2}e^x\sin x+\frac{1}{2}e^x\cos x+C,$$
where $C$ is a constant.

Example. Evaluate $\int e^x\sin xdx$.

Solution. In the following table, the first column represents $e^x$ and its derivatives, and the second column represents $\sin x$ and its integrals.
$$\begin{array}{ccc}
e^x & & \sin x\\
&\stackrel{+}{\searrow}&\\
e^x & & -\cos x\\
&\stackrel{-}{\searrow}&\\
e^x & & -\sin x.
\end{array}$$
This is similar to the above example. The first columns repeats the same function $e^x$, and the functions in the second column changes from $\sin x$ to $\cos x$ and to $\sin x$ again up to sign. So we stop there and write
$$\int e^x\sin xdx=-e^x\cos x+e^x\sin x-\int e^x\sin xdx.$$
Solving this for $\int e^x\sin xdx$, we obtain
$$\int e^x\sin xdx=-\frac{1}{2}e^x\cos x+\frac{1}{2}e^x\sin x+C,$$
where $C$ is a constant.

Example. Evaluate $\int e^{5x}\cos 8xdx$.

Solution. In the following table, the first column represents $e^{5x}$ and its derivatives, and the second column represents $\cos 8x$ and its integrals.
$$\begin{array}{ccc}
e^{5x} & & \cos 8x\\
&\stackrel{+}{\searrow}&\\
5e^{5x} & & \frac{1}{8}\sin 8x\\
&\stackrel{-}{\searrow}&\\
25e^{5x} & & -\frac{1}{64}\cos 8x.
\end{array}$$
The first columns repeats the same function $e^{5x}$ up to constant multiple, and the functions in the second column changes from $\cos 8x$ to $\sin 8x$ and to $\cos 8x$ again to constant multiple. This case also we do the same.
$$\int e^{5x}\cos 8xdx=\frac{1}{8}e^{5x}\sin 8x+\frac{5}{64}e^{5x}\cos 8x-\frac{25}{64}\int e^{5x}\cos 8xdx.$$
Solving this for $\int e^{5x}\cos 8xdx$, we obtain
$$\int e^{5x}\cos 8xdx=\frac{8}{89}e^{5x}\sin 8x+\frac{5}{89}e^{5x}\cos 8x+C,$$
where $C$ is a constant.

The evaluation of a definite integral by parts can be done as
\begin{equation}
\label{eq:intpart3}
\int_a^b f(x)g'(x)dx=[f(x)g(x)]_a^b-\int_a^b f'(x)g(x)dx.
\end{equation}

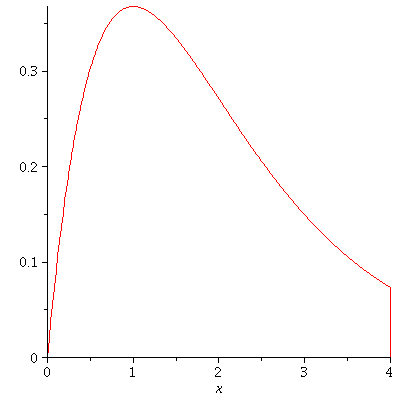
Example. Find the area of the region bounded by $y=xe^{-x}$ and the x-axis from $x=0$ to $x=4$.

The graph of y=xexp(-x), x=0..4

Solution. Let $u=x$ and $dv=e^{-x}dx$. Then $du=dx$ and $v=-e^{-x}$. Hence,
\begin{align*}
A&=\int_0^4 xe^{-x}dx\\
&=[-xe^{-x}]0^4+\int_0^4 e^{-x}dx\\
&=-4e^{-4}+[-e^{-x}]_0^4\\
&=1-5e^{-4}.
\end{align*}