Before we discuss homology groups, we review some basics of abelian group theory.
The group operation for an abelian group is denoted by $+$. The unit element is denoted by $0$.
Let $G_1$ and $G_2$ be abalian groups. A map $f: G_1\longrightarrow G_2$ is said to be a homomorphism if $$f(x+y)=f(x)+f(y),\ x,y\in G_1.$$ If $f$ is also a bijection (i.e one-to-one and onto), $f$ is called an isomorphism. If there is an isomorphism $f: G_1\longrightarrow G_2$, $G_1$ is said to be isomorphic to $G_2$ and we write $G_1\stackrel{f}{\cong} G_2$ or simply $G_1\cong G_2$.
Example. Define a map $f: \mathbb Z\longrightarrow\mathbb Z_2=\{0,1\}$ by $$f(2n)=0\ \mbox{and}\ f(2n+1)=1.$$ Then $f$ is a homomorphism.
A subset $H\subset G$ is a subgroup if it is a group with respect to the group operation of $G$.
Example. For any $k\in\mathbb N$, $k\mathbb Z=\{kn: n\in\mathbb Z\}$ is a subgroup of $\mathbb Z$.
Example. $\mathbb Z_2=\{0,1\}$ is not a subgroup of $\mathbb Z$.
Let $H$ be a subgroup of $G$. Define a relation on $G$ by $$\forall x,y\in G,\ x\sim y\ \mbox{if}\ x-y\in H.$$ Then $\sim$ is an equivalence relation on $G$. The equivalence class of $x\in G$ is denoted by $[x]$, i.e. \begin{eqnarray*}[x]&=&\{y\in G: y\sim x\}\\&=&\{y\in G: y-x\in H\}.\end{eqnarray*} Let $G/H$ be the quotient set $$G/H=\{[x]: x\in G\}.$$ Define an operation $+$on $G/H$ by $$[x]+[y]=[x+y],\ \forall [x],[y]\in G/H.$$ Then $G/H$ becomes an abelian group with this operation.
Example. $\mathbb Z/2\mathbb Z=\{[0],[1]\}$. Define $\varphi: \mathbb Z/2\mathbb Z\longrightarrow\mathbb Z_2$ by $$\varphi([0])=0\ \mbox{and}\ \varphi([1])=1.$$ Then $\mathbb Z/2\mathbb Z\cong\mathbb Z_2$. In general, for every $k\in\mathbb N$, $\mathbb Z/k\mathbb Z\cong\mathbb Z_k$.
Lemma 1. Let $f: G_1\longrightarrow G_2$ be a homomorphism. Then
(a) $\ker f=\{x\in G_1: f(x)=0\}=f^{-1}(0)$ is a subgroup of $G_1$.
(b) ${\mathrm im}f=\{f(x): x\in G_1\}$ is a subgroup of $G_2$.
Theorem 2 [Fundamental Theorem of Homomorphism]. Let $f: G_1\longrightarrow G_2$ be a homomorphism. Then $$G_1/\ker f\cong{\mathrm im}f.$$
Example. Let $f: \mathbb Z\longrightarrow\mathbb Z_2$ be defined by $$f(2n)=0,\ f(2n+1)=1.$$ Then $\ker f=2\mathbb Z$ and ${\mathrm im}f=\mathbb Z_2$. By Fundamental Theorem of Homomorphism, $$\mathbb Z/2\mathbb Z\cong\mathbb Z_2.$$
Take $r$ elements $x_1,x_2,\cdots,x_r$ of $G$. The elements of $G$ of the form $$n_1x_1+n_2x_2+\cdots+n_rx_r\ (n_i\in\mathbb Z,\ 1\leq i\leq r)$$ form a subgroup of $G$, which we denote $\langle x_1,\cdots,x_r\rangle$. $\langle x_1,\cdots,x_r\rangle$ is called a subgroup of $G$ generated by the generators $x_1,\cdots,x_r$. If $G$ itself is generated by finite lelements, $G$ is said to be finitely generated. If $n_1x_1+\cdots+n_rx_r=0$ is satisfied only when $n_1=\cdots=n_r=0$, $x_1,\cdots,x_r$ are said to be linearly independent.
Definition. If $G$ is fintely generated by $r$ linearly independent elements, $G$ is called a free abelian group of rank $r$.
Example. $\mathbb Z$ is a free abelian group of rank 1 generated by 1 (or $-1$).
Example. Let $\mathbb Z\oplus\mathbb Z=\{(m,n):m,n\in\mathbb Z\}$. The $\mathbb Z\oplus\mathbb Z$ is a free abelian group of rank 2 generated by $(1,0)$ and $0,1)$. More generally, $$\stackrel{r\ \mbox{copies}}{\overbrace{\mathbb Z\oplus\mathbb Z\oplus\cdots\oplus\mathbb Z}}$$ is a free abelian group of rank $r$.
Example. $\mathbb Z_2=\{0,1\}$ is fintely generated by 1 but is not free. $1+1=0$ so 1 is not linearly independent.
If $G=\langle x\rangle=\{0,\pm x,\pm 2x,\cdots\}$, $G$ is called a cyclic group. If $nx\ne 0$ $\forall n\in\mathbb Z\setminus\{0\}$, it is an infinite cyclic group. If $nx=0$ for some $n\in\mathbb Z\setminus\{0\}$, it is a finite cyclic group. Let $G=\langle x\rangle$ and let $f:\mathbb Z\longrightarrow G$ be a homomorphism defined by $f(k)=kx$, $k\in\mathbb Z$. $f$ is an epimorphism (i.e. onto homomorphism), so by Fundamental Theorem of Homomorphism, $$G\cong\mathbb Z/\ker f.$$ If $G$ is a finite group, then there exists the smallest positive integer $N$ such that $Nx=0$. Thus $$\ker f=\{0,\pm N,\pm 2N,\cdots\}=N\mathbb Z.$$ Hence $$G\cong\mathbb Z/N\mathbb Z\cong\mathbb Z_N.$$ If $G$ is an infinite cyclic group, $\ker f=\{0\}$. Hence, $$G\cong\mathbb Z/\{0\}\cong\mathbb Z.$$
Lemma 3. Let $G$ be a free abelian group of rank $r$, and let $H$ be a subgroup of $G$. Then one may always choose $p$ generators $x_1,\cdots,x_p$ out of $r$ generators of $G$ so that $k_1x_1,\cdots,k_px_p$ generate $H$. Hence, $$H\cong k_1\mathbb Z\oplus\cdots\oplus k_p\mathbb Z$$ and $H$ is of rank $p$.
Theorem 4 [Fundamental Theorem of Finitely Generated Abelian Groups] Let $G$ be a finitely generated abelian group with $m$ generators. Then $$G\cong\stackrel{r}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}\oplus \mathbb Z_{k_1}\oplus\cdots\oplus\mathbb Z_{k_p}$$ where $m=r+p$. The number $r$ is called the rank of $G$.
Proof. Let $G=\langle x_1, \cdots,x_m\rangle$ and let $f: \mathbb Z\oplus\cdots\oplus\mathbb Z\longrightarrow G$ be the surjective homomorphism $$f(n_1,\cdots,n_m)=n_1x_1+\cdots +n_mx_m.$$ Then by Fundamental Theorem of Homomorphism $$\mathbb Z\oplus\cdots\oplus\mathbb Z/\ker f\cong G.$$ $\stackrel{m}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}$ is a free abelian group of rank $m$ and $\ker f$ is a subgroup of $\mathbb Z\oplus\cdots\oplus\mathbb Z$, so by Lemma 3 $$\ker f\cong k_1\mathbb Z\oplus\cdots\oplus k_p\mathbb Z.$$ Define $\varphi:\stackrel{p}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}/k_1\mathbb Z\oplus \cdots\oplus k_p\mathbb Z\longrightarrow\mathbb Z/k_1\mathbb Z\oplus\cdots\oplus\mathbb Z/k_p\mathbb Z$ by $$\varphi((n_1,\cdots,n_p)+k_1\mathbb Z\oplus\cdots\oplus k_p\mathbb Z)=(n_1+k_1\mathbb Z,\cdots,n_p+k_p\mathbb Z).$$ Then $$\stackrel{p}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}/k_1\mathbb Z\oplus\cdots\oplus k_p\mathbb Z\stackrel{\varphi}{\cong}\mathbb Z/k_1\mathbb Z\oplus\cdots\oplus\mathbb Z/k_p\mathbb Z.$$ Hence, \begin{eqnarray*}G&\cong&\stackrel{m}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}/\ker f\\&\cong&\stackrel{m}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}/k_1\mathbb Z\oplus\cdots\oplus k_p\mathbb Z\\&\cong&\stackrel{m-p}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}\oplus\mathbb Z/k_1\mathbb Z\oplus\cdots\oplus Z/k_p\mathbb Z\\&\cong&\stackrel{m-p}{\overbrace{\mathbb Z\oplus\cdots\oplus\mathbb Z}}\oplus\mathbb Z_{k_1}\oplus\cdots\oplus\mathbb Z_{k_p}.\end{eqnarray*}

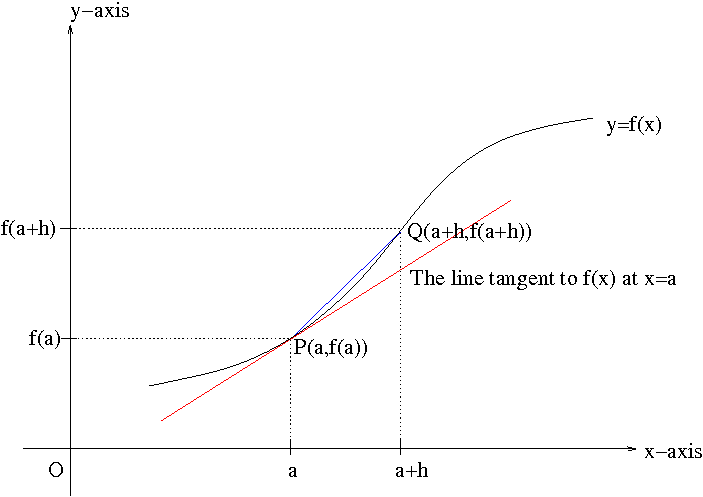
 This kind of discontinuity is called a removable discontinuity
This kind of discontinuity is called a removable discontinuity