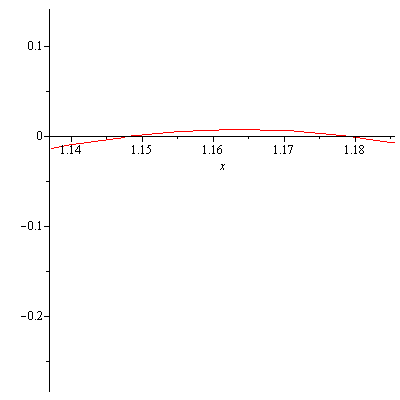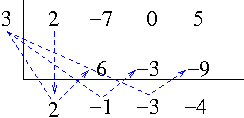As we studied here, once you know how to find at least one rational zero of a polynomial using long division or synthetic division you can find the rest of the zeros of the polynomial. In this note, we study how to find a rational zero of a polynomial if there is one. Let $P(x)=a_nx^n+\cdots +a_1x+a_0$ and suppose that $P(x)$ has a rational zero $\frac{p}{q}$. This means that by factor theorem $P(x)$ has a factor $x-\frac{p}{q}$ or equivalently a factor $qx-p$. That is, $P(x)=(qx-p)Q(x)$ where $Q(x)$ is a polynomial of degree $n-1$. Let us write $Q(x)=b_{n-1}x^{n-1}+\cdots+b_1x+b_0$. Then we see that $a_n=qb_{n-1}$ and $a_0=-pb_0$. This means that $q$ is a factor of the leading coefficient $a_n$ of $P(x)$ and $p$ is a factor of the constant term $a_0$ of $P(x)$. Hence we have the Rational Zero Theorem.

Rational Zero Theorem. Let $P(x)=a_nx^n+\cdots +a_1x+a_0$ be a polynomial with integer coefficients where $a_n\ne 0$ and $a_0\ne 0$. If $P(x)$ has a rationa zero $\frac{p}{q}$ then $q$ is a factor of $a_n$ and $p$ is a factor of $a_0$.

Here is the strategy to find a rational zero of a polynomial $P(x)$.

STEP 1. Use the rational zero theorem to find the all candidates for a rational zero of $P(x)$.

STEP 2. Test each candidate from STEP 1 to see if it is a rational zero using the factor theorem. Once you find one say $\frac{p}{q}$, stop and move to STEP 3

STEP 3. Use long division or synthetic division (easier) to divide $P(x)$ by $x-\frac{p}{q}$ to find the rest of the zeros.

STEP 4. If necessary (in the event $Q(x)$ from STEP 3 has a higher degree), repeat the process $Q(x)$ from STEP 1.

Example. Find all zeros of $P(x)=2x^3+x^2-13x+6$.

Solution. $a_0=2$ has factors $\pm 1$ and $\pm 2$. $a_0=6$ has factors $\pm 1,\pm 2,\pm3\pm 6$. Thus all the candidates for a rational zero are
$$\pm 1,\pm 2,\pm 3,\pm 6,\pm\frac{1}{2},\pm\frac{2}{2}=\pm 1,\pm\frac{3}{2},\pm\frac{6}{2}=\pm 3$$
Since $P(2)=0$, 2 is a rational zero. Using long division or synthetic division we find $Q(x)=2x^2+5x-3=(2x-1)(x+3)$. Therefore, all zeros of $P(x)$ are $-3,\frac{1}{2},2$.

Example. Find all zeros of $P(x)=x^4-5x^3+23x+10$.

Solution. $a_n=1$ has factors $\pm 1$ and $a_0=10$ has factors $\pm 1, \pm 2, \pm 5, \pm10$. So all the candidates for a rational zero are
$$\pm 1, \pm 2, \pm 5, \pm10$$
Since $P(5)=0$, 5 is a rational zero. Using long division or synthetic division we find $Q(x)=x^3-5x-2$. We cannot factor this cubic polynomial readily so we repeat the process. The leading coeffient 1 has factors $\pm 1$ and the constant term $-2$ has factors $\pm 1,\pm 2$ so all the candidates for a rational zero of $Q(x)$ are $\pm 1,\pm 2$. $Q(-2)=0$ so $-2$ is a rational zero of $Q(x)$ (and hence of $P(x)$ as well). Using one’s favorite division we find the quotient $x^2-2x-1$ which has two real zeros $1\pm\sqrt{2}$. Therefore, all zeros of $P(x)$ are
$5, -2, 1\pm\sqrt{2}$.

It would be convenient if we can estimate how many positive real zeros and how many negative zeros without actually factoring the polynomial. Here is a machinary just for that.

Descartes’ Rule of Signs

Let $P(x)$ be a polynomial with real coefficients.

1. The number of positive real zeros of $P(x)$ is either equal to the number of variations in sign in $P(x)$ or is less than that by an even number.
2. The number of negative real zeros of $P(x)$ is either equal to the number of variations in sign in $P(-x)$ or is less than that by an even number.

Example. $P(x)=3x^6+4x^5+3x^3-x-3$ has one variation in sign so there is one positive real zero. $P(-x)=3x^6-4x^5-3x^3+x-3$ has three variations in sign so there can be either three negative zeros or one negative zero.

Upper and Lower Bounds for Real Zeros

Let $P(x)$ be a polynomial with real coefficients.

1. If we divide $P(x)$ by $x-a$ ($a>0$) using synthetic division and if the row that contains the quotient and remainder has no negative entry, then $a$ is an upper bound for the real zeros of $P(x)$.
2. If we divide $P(x)$ by $x-b$ ($b<0$) using synthetic division and if the row that contains the quotient and remainder has entries that are alternatively nonpositive and nonnegative, then $b$ is a lower bound for the real zeros of $P(x)$.

Example. If we divide $P(x)=3x^6+4x^5+3x^3-x-3$ by $x-1$ then
$$1|\begin{array}{cccccc}
3 & 4 & 3 & 0 & -1 & -3\\
& 3 & 7 & 10 & 10 & 9\\
\hline
3 & 7 & 10 & 10 & 9 & 6
\end{array}$$
Since the row that contains quotient and remainder has no negative entries, 1 is an upper bound for real zeros of $P(x)$. If we divide $P(x)$ by $x-(-2)$ then
$$-2|\begin{array}{cccccc}
3 & 4 & 3 & 0 & -1 & -3\\
& -6 & 4 & -14 & 28 & -54\\
\hline
3 & -2 & 7 & -14 & 27 & -57
\end{array}$$
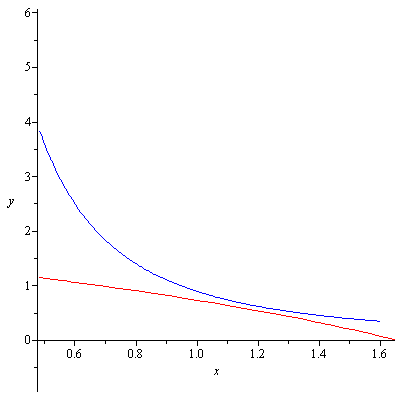
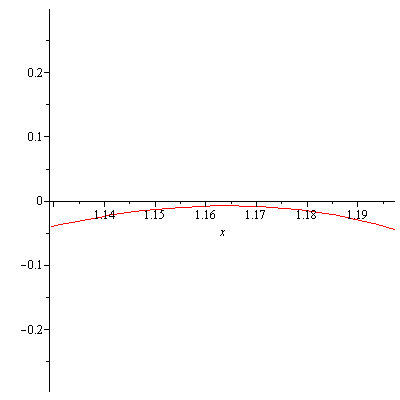
The entries of the row that contains the quotient and remainder are alternatively nonpositive and nonnegative, so $-2$ is a lower bound for real zeros of $P(x)$. $P(x)$ in fact does not have any integer zeros but the upper and lower bounds helps us graphically locate the real zeros of $P(x)$. Also they can be used as initial estimates for Newton’s method, a method that can find approximations to real zeros of a polynomial. Figure 1 shows that there is one positive real zero and one negative real zero of $P(x)$.

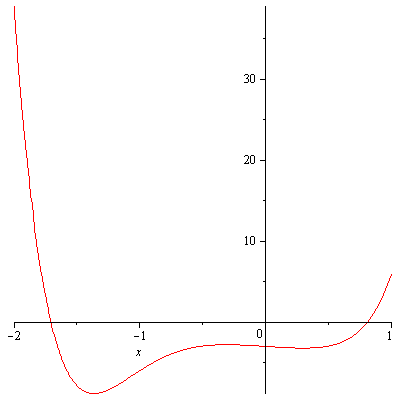
Real zeros of P(x)=3x^6+4x^5+3x^3-x-3

Polynomials are nice in the sense that they behave like numbers. For polynomials Division Algorithm works as well namely Given polynomials $P(x)$ and $D(x)\ne 0$ there exist unique polynomials $Q(x)$ and $R(x)$ such that
$$P(x)=D(x)Q(x)+R(x)$$
or
$$\frac{P(x)}{D(x)}=Q(x)+\frac{R(x)}{D(x)}$$
$P(x)$, $D(x)$, $Q(x)$, and $R(x)$ are called, respectively, the dividend, divisor, quptient and remainder. There are two ways to divide a polynomial by another polynomial. The first one is the familiar long division and it works the same way we do with numbers.

Example. Let $P(x)=8x^4+6x^2-3x+1$ and $D(x)=2x^2-x+2$. Find polynomials $Q(x)$ and $R(x)$ such that $P(x)=D(x)Q(x)+R(x)$.

Solution.

Long division

Hence $Q(x)=4x^2+2x$ and $R(x)=-7x+1$.

The other method is called synthetic division. This method cannot be used for any polynomial divisions, however it works great when the divisor is a linear polynomial and is easier than long division. Synthetic division uses only coefficients without including variables as shown in the following example.

Example. Using synthetic division divide $2x^3-7x^2+5$ by $x-3$.

Solution.

Synthetic division

Hence we have $Q(x)=2x^2-x-3$ and $R=-4$.

If a polynomial $P(x)$ is divided by a linear polynomial $x-c$, by division algorithm $P(x)$ can be written as
$$P(x)=(x-c)Q(x)+R$$
for some $Q(x)$ and $R$. So, $P(c)=R$ and hence we obtain the Remainder Theorem.

Remainder Theorem. If a polynomial $P(x)$ is divided by $x-c$, then the remainder is $P(c)$.

Example. Let $P(x)=3x^5+5x^4-4x^3+7x+3$. Use the remainder theorem to find the remainder when $P(x)$ is divided by $x+2$.

Solution. $R=P(-2)=5$.

As a corollary of the remainder theorem we have

Factor Theorem. $c$ is a zero of $P(x)$ if and only if $x-c$ is a factor of $P(x)$.

Example. Let $P(x)=x^3-7x+6$. Show that $P(1)=0$ and use this information to factor $P(x)$ completely.

Solution. Dividing $P(x)$ by $x-1$ (using long division or synthetic division) we find $Q(x)=x^2+x-6$ and $R=0$ (of course as we expected). So,
\begin{align*}
P(x)&=(x-1)(x^2+x-6)\\
&=(x-1)(x-2)(x+3)
\end{align*}

Example. Find a polynomial of degree 4 that has zeros $-3$, 0, 1, and 5.

Solution. Such a polynomial would have $x+3$, $x$, $x-1$, and $x-5$ for its factors by the factor theorem. So the simplest one is
$$P(x)=(x+3)x(x-1)(x-5)=x^4-3x^3-13x^2+15x$$