Polynomials are nice in the sense that they behave like numbers. For polynomials Division Algorithm works as well namely Given polynomials $P(x)$ and $D(x)\ne 0$ there exist unique polynomials $Q(x)$ and $R(x)$ such that
$$P(x)=D(x)Q(x)+R(x)$$
or
$$\frac{P(x)}{D(x)}=Q(x)+\frac{R(x)}{D(x)}$$
$P(x)$, $D(x)$, $Q(x)$, and $R(x)$ are called, respectively, the dividend, divisor, quptient and remainder. There are two ways to divide a polynomial by another polynomial. The first one is the familiar long division and it works the same way we do with numbers.

Example. Let $P(x)=8x^4+6x^2-3x+1$ and $D(x)=2x^2-x+2$. Find polynomials $Q(x)$ and $R(x)$ such that $P(x)=D(x)Q(x)+R(x)$.

Solution.

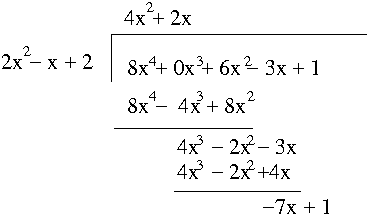
Long division

Hence $Q(x)=4x^2+2x$ and $R(x)=-7x+1$.

The other method is called synthetic division. This method cannot be used for any polynomial divisions, however it works great when the divisor is a linear polynomial and is easier than long division. Synthetic division uses only coefficients without including variables as shown in the following example.

Example. Using synthetic division divide $2x^3-7x^2+5$ by $x-3$.

Solution.

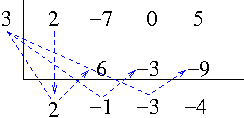
Synthetic division

Hence we have $Q(x)=2x^2-x-3$ and $R=-4$.

If a polynomial $P(x)$ is divided by a linear polynomial $x-c$, by division algorithm $P(x)$ can be written as
$$P(x)=(x-c)Q(x)+R$$
for some $Q(x)$ and $R$. So, $P(c)=R$ and hence we obtain the Remainder Theorem.

Remainder Theorem. If a polynomial $P(x)$ is divided by $x-c$, then the remainder is $P(c)$.

Example. Let $P(x)=3x^5+5x^4-4x^3+7x+3$. Use the remainder theorem to find the remainder when $P(x)$ is divided by $x+2$.

Solution. $R=P(-2)=5$.

As a corollary of the remainder theorem we have

Factor Theorem. $c$ is a zero of $P(x)$ if and only if $x-c$ is a factor of $P(x)$.

Example. Let $P(x)=x^3-7x+6$. Show that $P(1)=0$ and use this information to factor $P(x)$ completely.

Solution. Dividing $P(x)$ by $x-1$ (using long division or synthetic division) we find $Q(x)=x^2+x-6$ and $R=0$ (of course as we expected). So,
\begin{align*}
P(x)&=(x-1)(x^2+x-6)\\
&=(x-1)(x-2)(x+3)
\end{align*}

Example. Find a polynomial of degree 4 that has zeros $-3$, 0, 1, and 5.

Solution. Such a polynomial would have $x+3$, $x$, $x-1$, and $x-5$ for its factors by the factor theorem. So the simplest one is
$$P(x)=(x+3)x(x-1)(x-5)=x^4-3x^3-13x^2+15x$$