For a fair coin, if we toss it a very large number of times, nearly half the time we will get heads and half the time we will get tails. So, we can say the probability of getting heads is equal to the probability of getting tails as $\frac{1}{2}$.

Now consider the simultaneous tossing of $N$ coins. For $N=2$, there are four possible outcomes: $HH$, $HT$, $TH$, and $TT$. The probabilities of getting 2 heads, 1 head, and no head are, respectively, $\frac{1}{4}$, $\frac{2}{4}=\frac{1}{2}$, $\frac{1}{4}$. The number of ways we can get $n$ heads (consequently $N-n$ tails) is
$$\frac{N!}{n!(N-n)!}$$
The probability $p$ of getting $n$ heads is then
\begin{equation}
\label{eq:binomial}
p=\frac{N!}{n!(N-n)!2^N}
\end{equation}
Let us consider
$$\ln p=\ln\frac{N!}{n!(N-n)!2^N}=\ln N!-\ln n!-\ln(N-n)!-N\ln 2$$
Using the Stirling’s formula
$$\ln N!\approx N\ln N-N$$
we obtain
$$\ln p\approx -N\left[\frac{n}{N}\ln\frac{n}{N}+\left(1-\frac{n}{N}\right)\ln\left(1-\frac{n}{N}\right)+\ln 2\right]$$
For very large $N$, $x=\frac{n}{N}$ can be considered to be continuous.
$$\ln p\approx -N[x\ln x+(1-x)\ln(1-x)]$$
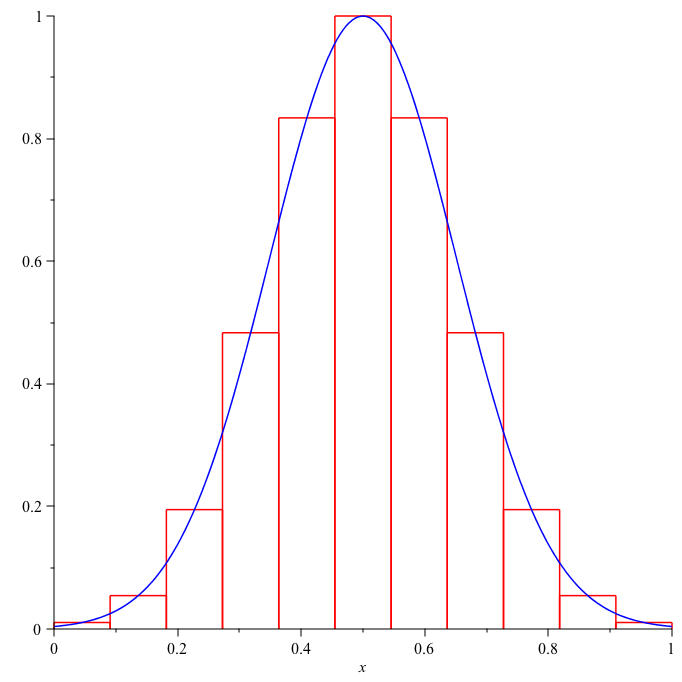
$\ln p$ has only one critical point at $x=\frac{1}{2}$ and the second derivative of $\ln p$ at $x=\frac{1}{2}$ is negative. So $\ln p$ (and consequently $p$) assumes a maximum at $x=\frac{1}{2}$. Expanding $\ln p$ at $x=\frac{1}{2}$, we have
$$\ln p\approx -2N\left(x-\frac{1}{2}\right)^2$$
or
$$p\approx\exp\left[-2N\left(x-\frac{1}{2}\right)^2\right]$$
As seen clearly, the standard deviation from $x=\frac{1}{2}$ is $\frac{1}{2\sqrt{N}}$.

Thus far, we have considered equal probabilities. Suppose that we have a coin with a probability of $q$, $0<q<1$ for heads. Then the probability of getting $n$ heads when $N$ coins are tossed is
\begin{equation}
\label{eq:binomial2}
\frac{N!}{n!(N-n)!}q^n(1-q)^{N-n}
\end{equation}
$q=\frac{1}{2}$ reduces \eqref{eq:binomial2} to \eqref{eq:binomial}. Note that the probability in $\eqref{eq:binomial}$ peaks at $x=q$ and the standard deviation from $x=q$ is the same.

We now consider events with more than two outcomes. For example, rolling a dice has six possible outcomes.
Suppose that we want to distribute $N$ particles into $K$ boxes in such a way that $n_i$ particles go into box $i$. How many ways are there to do this? There are $\frac{N!}{n_1!(N-n_1)!}$ ways to choose $n_1$ particles out of $N$ particles. Then there are $\frac{(N-n_1)!}{n_2!(N-n_1-n_2)!}$ ways to choose $n_2$ particles out of remaining $N-n_1$ particles, and so on and so forth. Hence, the number of ways to distribute $n_1$ particles in box 1, $n_2$ particles in box 2, …, $n_K$ particles in box $K$ is
\begin{align*} \frac{N!}{n_1!(N-n_1)!}\frac{(N-n_1)!}{n_2!(N-n_1-n_2)!}&\frac{(N-n_1-n_2)!}{n_3!(N-n_1-n_2-n_3)!}\cdots\\ &\frac{(N-n_1-n_2-\cdots-n_{K-1})!}{n_K!}\\ &=\frac{N!}{n_1!n_2!\cdots n_K!}\\ &=N!\Pi_{i=1}^K\frac{1}{n_i!}, \end{align*}
$\sum_{i=1}^Kn_i=N$.