The notion of an angle is so basic (and we use it everyday indeed) that anyone with basic math knowledge would know what it is, right? Turns out it is not the case. I often was surprised to find out that even math majors in upper level math courses can’t explain what an angle is. They commonly answer like this: First draw two rays that intersect at a point and then draw an arc between them. They would call this arc an angle.
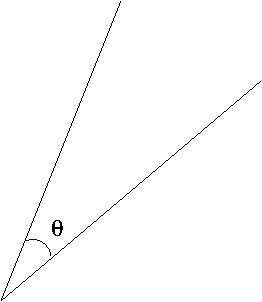
But then there can be so many different choices of arcs between two such rays. So which arc is an angle? The arc that defines an angle is one that is a part of the unit circle.
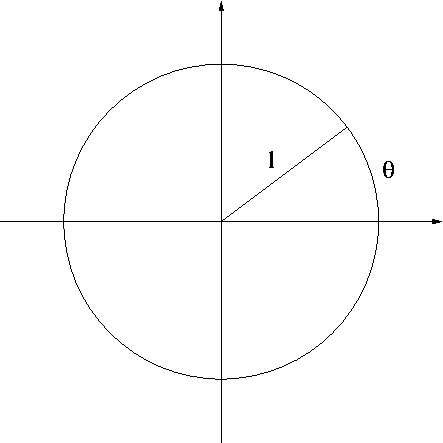
A measurement of an angle requires a unit. It is speculated that the degree measurement was invented by ancient Sumerians. Sumer is the earliest known civilization which was in southern Mesopotamia (modern day southern Iraq) and it dates back before 3,000 B.C. The biblical Genesis appears to have originated from Sumerian creation myth Enûma Eliš which predates Torah (Hebrew Bible). The first man’s name is Adamu and it does have the story of the Great Deluge. Sumerians had own writing system using cuneiform (wedge-shaped marks on clay tablets) and they built massive structures called ziggurats. Amazingly, those ziggurats still remain to this day in modern day Iraq. Sumerians possessed highly advanced level of knowledge in math and science including astronomy. Here is how they introduced the degree unit of angle measurement: Divide the unit circle into 360 equal sections (imagine 360 equal pizza slices). The length of the arc of each section is then defined to be $1^\circ$ and the circumference of the unit circle is $360^\circ$.
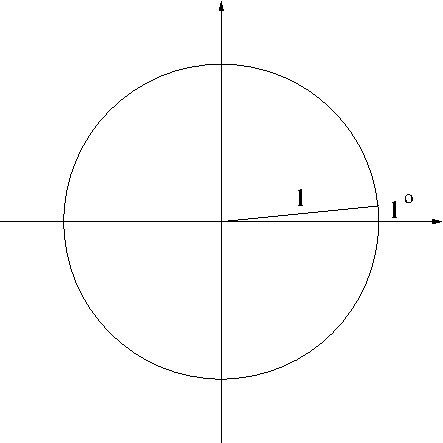
Why the number 360? A common speculation is that Sumerians thought 1 year = 360 days, a complete rotation. Oh yes, they appear to have known that Earth is rotating around the Sun on a circular (actually elliptic) orbit. I have a different theory though. I do believe that Sumerians actually knew 1 year = 365 days. But if they used the number 365 to define $1^\circ$, it would have been an awfully ugly and inconvenient angle measurement. I believe that they knew this and used 360 instead.
On the other hand, you know from elementary geometry that the circumference of a circle with radius $r$ is $2\pi r$. So the unit circle has circumference $2\pi$. Hence we must have $$2\pi=360^\circ$$ However, something looks really awkward. The right hand side has a unit while the left hand side doesn’t. So it was given a unit called radian (denoted by rad), i.e. $$2\pi\ \mathrm{rad}=360^\circ$$ or $$\pi\ \mathrm{rad}=180^\circ$$ Note that 1 rad is merely a number (it’s same as the number 1) while $1^\circ$ is not. So in calculus we don’t use degree angle measurement but only use radian angle measurement.
Given an angle $\theta$, there is a corresponding point $(x,y)$ on the unit circle as shown in Figure 4.
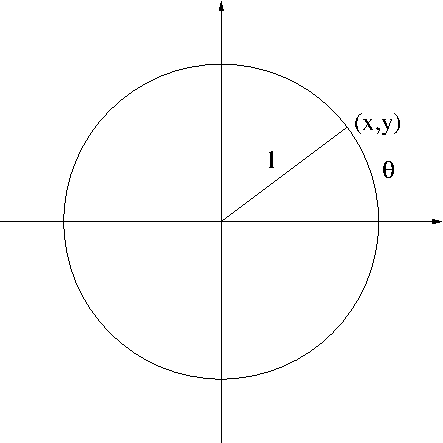
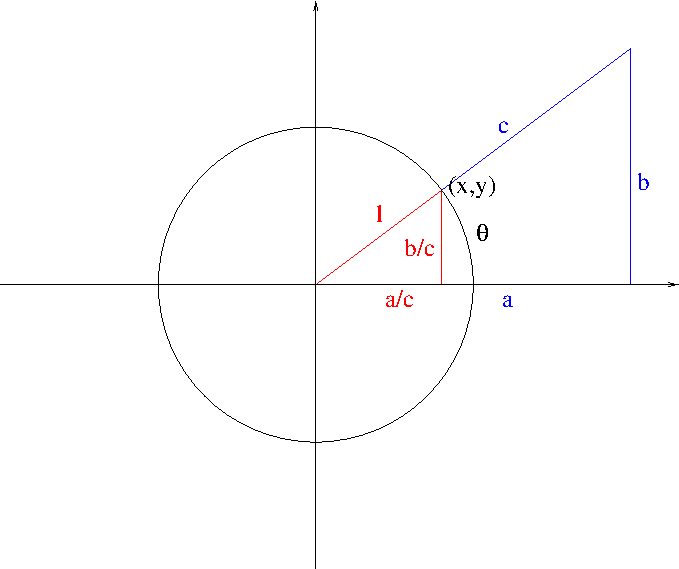
In order to make this correspondence more transparent, one may want to represent $x$ and $y$ in terms of the angle $\theta$. This is how cosine and sine of an angle were introduced: \begin{equation}\label{eq:trig}x=\cos\theta,\ y=\sin\theta\end{equation} The unit circle centered at the origin satisfies the equation \begin{equation}\label{eq:circ}x^2+y^2=1\end{equation} Using \eqref{eq:trig}, \eqref{eq:circ} can be written as \begin{equation}\label{eq:circ2}(\cos\theta)^2+(\sin\theta)^2=1\end{equation} But this looks a bit ugly, so a better looking notations were introduced: $$\cos^2\theta:=(\cos\theta)^2,\ \sin^2\theta:=(\sin\theta)^2$$ Thereby, \eqref{eq:circ2} is written as $$\cos^2\theta+\sin^2\theta=1$$ For an obvious reason, $\cos\theta$ and $\sin\theta$ along with $\tan\theta$, $\cot\theta$, $\sec\theta$, and $\csc\theta$ are called circular functions. I bet though most of you who are reading this have never heard of the name circular functions. The reason is that nowadays those quantities are defined more commonly (and shamefully) by using right triangles. (See Figure 5.) Hence they are called by more familiar name, trigonometic functions.
An ancient Babylonian clay tablet which dates to 3,700 years ago, around the time when King Hammurabi ruled the Babylonian Empire, was recently decoded by scientists. It turns out that the tablet contains the oldest trigonometric table. In general, trigonometry is thought to have originated by Greek astronomer Hipparchu around 120 B.C. This remarkable discovery tells that ancient Babylonians already have known trigonometry 1,000 years before Greeks did. More details about the clay tablet can be read here.
