Related rates problems often involve (context-wise) real-life applications of the chain rule/implicit differentiation. Here are some of the examples that are commonly seen in calculus textbooks.

Example. Car A is traveling west at 50mi/h and car B is traveling north at 60mi/h. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 mi and car B is 0.4 mi from the intersection?

Solution.

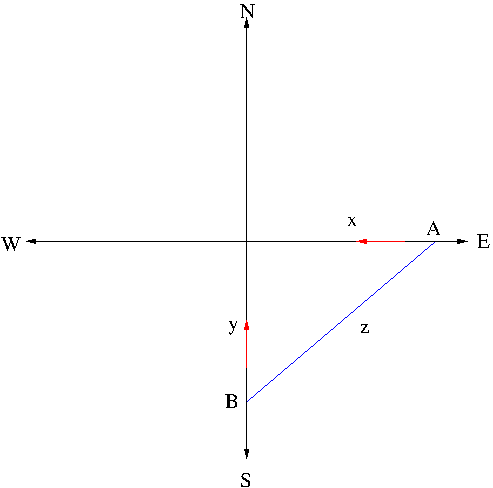
Denote by $x$ and $y$ the distances from the intersection to car A and to car B, respectively. Then we have $\frac{dx}{dt}=-50$mi/h and $\frac{dy}{dt}=-60$mi/h. Let us denote $z$ the distance between $A$ and $B$. Then by Pythagorean law we have $$z^2=x^2+y^2$$ Differentiating this with respect to $t$, we obtain $$z\frac{dz}{dt}=x\frac{dx}{dt}+y\frac{dy}{dt}$$ and thus \begin{align*}\frac{dz}{dt}&=\frac{1}{z}\left[x\frac{dx}{dt}+y\frac{dy}{dt}\right]\\&=\frac{1}{0.5}[0.3(-50)+0.4(-60)]=-78\mathrm{mi/h}\end{align*}

Example. Air is being pumped into a spherical balloon so that its volume increases at a rate of $100\mathrm{cm}^3/\mathrm{s}$. How fast is the radius of the balloon increasing when the diameter is 50 cm?

Solution. Let $V$ and $r$ denote the volume and the radius of the spherical balloon. Then $V=\frac{4}{3}\pi r^3$. Differentiating this with respect to $t$, we obtain $$\frac{dV}{dt}=4\pi r^2\frac{dr}{dt}$$ So, \begin{align*}\frac{dr}{dt}&=\frac{1}{4\pi r^2}\frac{dV}{dt}\\&=\frac{1}{4\pi(25)^2}100\\&=\frac{1}{25\pi}\mathrm{cm/s}\end{align*}

Example. Gravel is being dumped from a conveyor belt at a rate of $30 \mathrm{ft}^3/\mathrm{min}$ and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are the same. How fast is the height of the pile increasing when the pile is 10 ft high?

Solution. The cross section of the gravel pile is shown in the figure below.

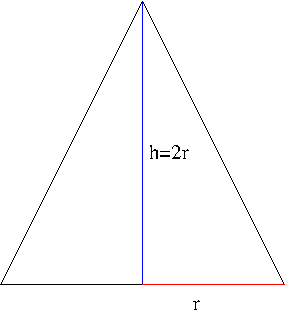
The amount of gravel dumped is the same as the volume of the cone. Let us denote the volume by $V$, its base radius by $r$, and its height by $h$. Then $V=\frac{1}{3}\pi r^2h$. Since $h=2r$, $V$ can be written as $$V=\frac{1}{12}\pi h^3$$ Differentiating this with respect to $t$, we obtain $$\frac{dV}{dt}=\frac{1}{4}\pi h^2\frac{dh}{dt}$$ So, we have \begin{align*}\frac{dh}{dt}&=\frac{4}{\pi h^2}\frac{dV}{dt}\\&=\frac{4}{\pi(10)^2}(30)=\frac{1.2}{\pi}\mathrm{ft/min}\approx 0.38\mathrm{ft/min}\end{align*}

Example. A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 ft/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall?

Solution.

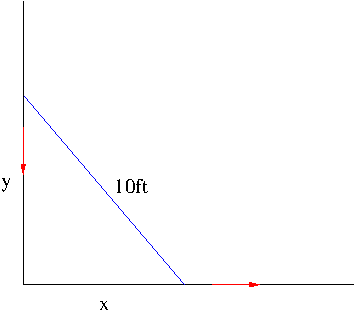
Let us denote by $x$ and $y$ the distance from the wall to the bottom of the ladder and the distance from the top of the ladder to the floor, respectively. By Pythagorean law, we have $x^2+y^2=100$. Differentiating this with respect to $t$, we obtain $$x\frac{dx}{dt}+y\frac{dy}{dt}=0$$ Hence, we have \begin{align*}\frac{dy}{dt}&=-\frac{x}{y}\frac{dx}{dt}\\&=-\frac{6}{8}(1)=-\frac{3}{4}\mathrm{ft/s}\end{align*}

Example. A water tank has the shape of an inverted circular cone with base radius 2m and heigh 4 m. If water is being pumped into the tank at a rate of $2 \mathrm{m}^3/\mathrm{min}$, find the rate at which the water level is rising when the water is 3 m deep.

Solution. The cross section of the water tank is shown in the figure below.

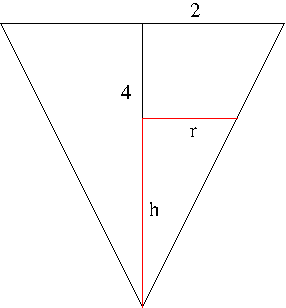
The amount of water $V$ when the water level is $h$ and the surface radius is $r$ is $V=\frac{1}{3}\pi r^2h$. From the above figure we have the following ratio holds $$\frac{2}{4}=\frac{r}{h}$$ i.e. $r=\frac{h}{2}$. SO $V$ can be written as $$V=\frac{1}{12}\pi h^3$$ Differentiating this with respect to $t$, we obtain $$\frac{dV}{dt}=\frac{1}{4}\pi h^2\frac{dh}{dt}$$ Hence, \begin{align*}\frac{dh}{dt}&=\frac{4}{\pi h^2}\frac{dV}{dt}\\&=\frac{4}{\pi(3)^2}(2)\\&=\frac{8}{9\pi}\mathrm{m/min}\approx 0.28\mathrm{m/min}\end{align*}

Example. A street light is at the top of a 15 feet tall pole. A 6 feet tall woman walks away from the pole with a speed of 5 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 45 feet from the base of the pole?

Solution. Let $x$ be the distance from the light pole to the woman and $y$ be the distance from the light pole to the tip of her shadow as shown in the figure below.

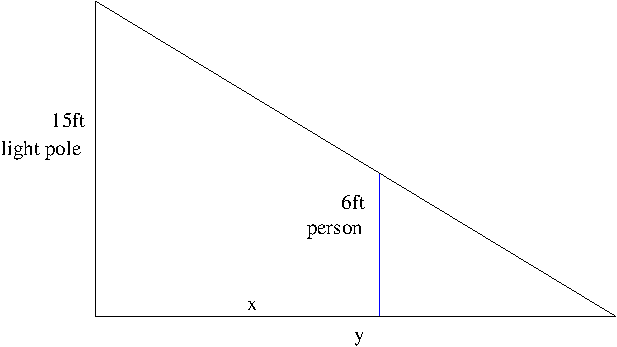
By similar triangles, we have $\frac{15}{y}=\frac{6}{y-x}$. Solving this equation for $y$, we obtain $y=\frac{5}{3}x$. Differentiating this with respect to $t$, we find how fast the tip of her shadow is moving: $$\frac{dy}{dt}=\frac{5}{3}\frac{dx}{dt}=\frac{25}{3}\mathrm{ft/s}$$ As seen regardless of how far the woman is from the pole, the speed of the tip is constant.

Example. The fish population, $N$, in a small pond depends on the amount of algae, $a$ (measured in pounds), in it. The equation modeling the fish population is given by $N=(3a^2-20a+26)^4$. If the amount of algae is increasing at a rate of 2 lb/week, at what rate is the fish population changing when the pond contains 5 lb of algae?

Solution. By the chain rule, we obtain \begin{align*}\frac{dN}{dt}&=4(3a^2-20a+26)^3\left(6a\frac{da}{dt}-20\frac{da}{dt}\right)\\&=4(3a^2-20a+26)^3(6a-20)\frac{da}{dt}\end{align*} $\frac{da}{dt}=2$lb/week, so when $a=5$lb, $\frac{dN}{dt}$ is $$\frac{dN}{dt}=4(3(5)^2-20(5)+26)^3(6(5)-20)(2)=-80\ \mathrm{lb/week}$$ What this means is that the fish population is decreasing by 80 lb/week at the instant when the pond contains 5 lb of algae.

Example. The retail price per gallon of gasoline is increasing at \$0.02 per week. The demand equation is given by $$10p-\sqrt{356-x^2}=0$$ where $p$ is the price per gallon (in dollars), when $x$ million gallons are demanded. At what rate is the revenue changing when 10 million gallons are demanded?

Solution. The total revenue $R$ is given by the equation $$R=xp$$ Differentiating this equation with respect to $t$, we obtain $$\frac{dR}{dt}=\frac{dx}{dt}p+x\frac{dp}{dt}$$ The only quantity we don’t have to calculate $\frac{dR}{dt}$ is $\frac{dx}{dt}$. To find it, let us differentiate the demand function with respect to $x$. By the chain rule, we obtain $$10\frac{dp}{dt}+\frac{x}{\sqrt{351-x^2}}\frac{dx}{dt}=0$$ When $x=10$ million gallons, with $\frac{dp}{dt}=0.02$, we find from this equation that $$\frac{dx}{dt}=-0.02\sqrt{256}=-0.02\cdot 16= -0.32\ \mbox{million gallons/week}$$ When $x=10$, from the demand function, we find $p$ as $$p=\frac{\sqrt{256}}{10}=\frac{16}{10}=1.6$$ Therefore, the rate of change of revenue when 10 million gallons of gasoline is demanded is $$\frac{dR}{dt}=-0.32(1.6)+10(0.02)=-0.312$$ What this means is that the revenue is decreasing by about 0.31 million dollars per week when the price increases 0.02 dollars per week (consequently the demand decreases by 0.32 million gallons per week as we saw earlier).

Example. A plane flying with a constant speed of 29 km/min passes over a ground radar station at an altitude of 13 km and climbs at an angle of 20 degrees. At what rate is the distance from the plane to the radar station increasing 3 minutes later?

Solution. First, take a look at the following picture

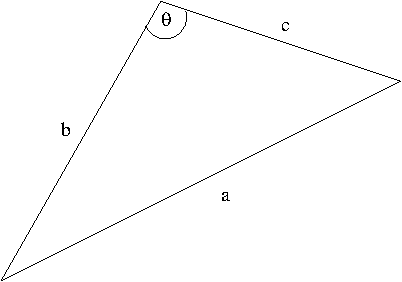
The law of cosine says that the sides $a$, $b$, $c$ and the angle $\theta$ are related by $$a^2=b^2+c^2-2bc\cos\theta$$

The question above can be pictorially represented as the following sketch

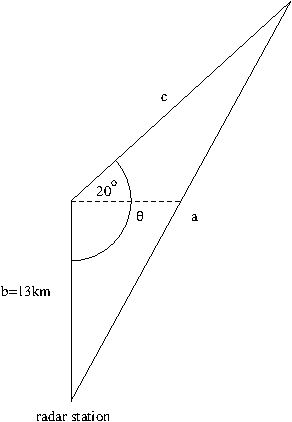
Using the law of cosine with $b=13$ km, we have $$a^2=13^2+c^2-2\cdot 13\cdot c\cdot\cos\left(\frac{11}{18}\pi\right)$$ Here, the angle $\theta$ is given by $\theta=90^\circ+20^\circ=110^\circ=\frac{11}{18}\pi$$ (Note: for this question, you can use degree instead of radian but in that case make sure that your calculator is set to use degree angle measurement.) Since we are to find $\frac{da}{dt}$, differentiate the above equation with respect to $t$: $$2a\frac{da}{dt}=2c\frac{dc}{dt}-2\cdot 13\frac{dc}{dt}\cos\left(\frac{11}{18}\pi\right)$$ Since the airplane is flying along the side $c$ at the constant speed 29 km/min, it would have traveled $c=29\cdot 3=87$ km in three minutes. Thus, $$a=\sqrt{13^2+87^2-2\cdot 13\cdot 87\cos\left(\frac{11}{18}\pi\right)}=92.2586$$ and hence $\frac{da}{dt}$ in three minutes is \begin{align*}\frac{da}{dt}&=\frac{c}{a}\frac{dc}{dt}-\frac{13}{a}\frac{dc}{dt}\cos\left(\frac{11}{18}\pi\right)\\&=\frac{1}{a}\frac{dc}{dt}\left(c-13\cos\left(\frac{11}{18}\pi\right)\right)\\&=\frac{1}{92.2586}29\left(87-13\cos\left(\frac{11}{18}\pi\right)\right)\\&=28.7447\ \mathrm{km/min}\end{align*}