When the integrand contains $\sqrt{a^2+x^2}$, $\sqrt{a^2-x^2}$ or $\sqrt{x^2-a^2}$ and the integral cannot be evaluated by a simple substitution, the following trigonometric substitutions may come in handy:

1. For $\sqrt{a^2+x^2}$, use $x=a\tan\theta$ with $-\frac{\pi}{2}<\theta<\frac{\pi}{2}$. Accordingly $dx=a\sec^2\theta d\theta$ and $a^2+x^2=a^2\sec^2\theta$.
2. For $\sqrt{a^2-x^2}$, use $x=a\sin\theta$ with $-\frac{\pi}{2}\leq x\leq\frac{\pi}{2}$. Accordingly $dx=a\cos\theta d\theta$ and $a^2-x^2=a^2\cos^2\theta$. Note: You can also use the substitution $x=a\cos\theta$ with $0\leq\theta\leq\pi$. Accordingly $dx=-a\sin\theta d\theta$ and $a^2-x^2=a^2\sin^2\theta$.
3. For $\sqrt{x^2-a^2}$, use $x=a\sec\theta$ with $0\leq\theta<\frac{\pi}{2}$ or $\pi\leq\theta<\frac{3\pi}{2}$. Accordingly $dx=a\sec\theta\tan\theta d\theta$ and $x^2-a^2=a^2\tan^2\theta$.

Example. Evaluate $\int\frac{dx}{\sqrt{4+x^2}}$.

Solution. Let $x=2\tan\theta$. Then $dx=2\sec^2\theta d\theta$ and $4+x^2=4\sec^2\theta$. So \begin{align*}\int\frac{dx}{\sqrt{4+x^2}}&=\int\frac{2\sec^2\theta d\theta}{2|\sec\theta|}\\&=\int\sec\theta d\theta\ \left(\sec\theta>0\ \mbox{for}\ -\frac{\pi}{2}<\theta<\frac{\pi}{2}\right)\\&=\ln|\sec\theta+\tan\theta|+C’\end{align*} SInce $\tan\theta=\frac{x}{2}$ one may consider the triangle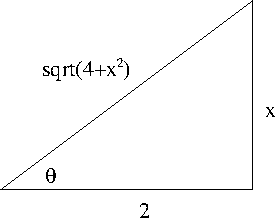

Hence $$\int\frac{dx}{\sqrt{4+x^2}}=\ln|\sqrt{4+x^2}+x|+C$$ where $C=C’-\ln 2$.

Example. Evaluate $\int\frac{x^2}{\sqrt{9-x^2}}dx$.

Solution. Let $x=3\sin\theta$. Then $dx=3\cos\theta d\theta$ and $9-x^2=9\cos^2\theta$. \begin{align*}\int\frac{x^2}{\sqrt{9-x^2}}dx&=\int\frac{9\sin^2\theta(3\cos\theta d\theta)}{3|\cos\theta|}\\&=9\int\sin^2\theta d\theta\ \left(\cos\theta>0\ \mbox{for}\ -\frac{\pi}{2}<\theta<\frac{\pi}{2}\right)\\&=9\int\frac{1-\cos 2\theta}{2}d\theta\\&=\frac{9}{2}(\theta-\sin\theta\cos\theta)+C\\&=\frac{9}{2}\left(\sin^{-1}\frac{x}{3}-\frac{x}{3}\frac{\sqrt{9-x^2}}{3}\right)+C\\&=\frac{9}{2}\sin^{-1}\frac{x}{3}-\frac{x}{2}\sqrt{9-x^2}+C\end{align*}

Example. Evaluate $\int\frac{dx}{\sqrt{25x^2-4}}$.

Solution. $\int\frac{dx}{\sqrt{25x^2-4}}=\frac{1}{5}\int\frac{dx}{\sqrt{x^2-\left(\frac{2}{5}\right)^2}}$. Let $x=\frac{2}{5}\sec\theta$. Then $dx=\frac{2}{5}\sec\theta\tan\theta d\theta$ and $x^2-\left(\frac{2}{5}\right)^2=\frac{4}{25}\tan^2\theta$. \begin{align*}\int\frac{dx}{\sqrt{25x^2-4}}&=\frac{1}{5}\int\frac{dx}{\sqrt{x^2-\left(\frac{2}{5}\right)^2}}\\&=\frac{1}{5}\int\frac{\frac{2}{5}\sec\theta\tan\theta d\theta}{5\left(\frac{2}{5}\right)\tan\theta}\ \left(\tan\theta>0\ \mbox{for}\ 0<\theta<\frac{\pi}{2}\right)\\&=\frac{1}{5}\int\sec\theta d\theta\\&=\frac{1}{5}\ln|\sec\theta +\tan\theta|+C’\\&=\frac{1}{5}\ln|5x+\sqrt{25x^2-4}|+C\end{align*} where $C=C’-\frac{\ln 2}{5}$.

Example. Evaluate $\int\sqrt{1+x^2}dx$.

Solution. Let $x=\tan\theta$. Then $dx=\sec^2\theta d\theta$ and $1+x^2=\sec^2\theta$. \begin{align*}\int\sqrt{1+x^2}dx&=\int\sec^3\theta d\theta\\&=\frac{1}{2}\sec\theta\tan\theta+\frac{1}{2}\ln|\sec\theta+\tan\theta|+C\\&=\frac{1}{2}x\sqrt{1+x^2}+\frac{1}{2}\ln|x+\sqrt{1+x^2}|+C\end{align*} The integration $$\int\sec^3\theta d\theta=\frac{1}{2}\sec\theta\tan\theta+\frac{1}{2}\ln|\sec\theta+\tan\theta|+C$$ was discussed here.

Example. Evaluate $\int\frac{\sqrt{1+x^2}}{x}dx$.

Solution. Let $x=\tan\theta$. Then $dx=\sec^2\theta d\theta$ and $1+x^2=\sec^2\theta$. \begin{align*}\int\frac{\sqrt{1+x^2}}{x}dx&=\int\frac{\sec^3\theta}{\tan\theta}d\theta\\&=\int\frac{\sec\theta\sec^2\theta}{\tan\theta}d\theta\\&=\int\frac{\sec\theta(1+\tan^2\theta)}{\tan\theta}d\theta\\&=\int\frac{\sec\theta}{\tan\theta}d\theta+\int\sec\theta\tan\theta d\theta\\&=\int\csc\theta d\theta+\int\sec\theta\tan\theta d\theta\\&=-\ln|\csc\theta+\cot\theta|+\sec\theta+C\\&=-\ln\left|\frac{\sqrt{1+x^2}}{x}+\frac{1}{x}\right|+\sqrt{1+x^2}+C\end{align*}

Example. Find the area enclosed by the ellipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

Solution. The ellipse in the first quadrant is given by the function $y=\frac{b}{a}\sqrt{a^2-x^2}$, $0\leq x\leq a$. So the area is \begin{align*}A&=4\int_0^a\frac{b}{a}\sqrt{a^2-x^2}dx\\&=4\frac{b}{a}\int_0^{\frac{\pi}{2}}a\cos\theta(a\cos\theta d\theta)\ (x=a\sin\theta$)\\&=4ab\int_0^{\frac{\pi}{2}}\cos^2\theta d\theta\\&=4ab\int_0^{\frac{\pi}{2}}\frac{1+\cos 2\theta}{2}d\theta\\&=\pi ab\end{align*}