Suppose that a continuously differentiable curve $y=f(x)\geq 0$ on $[a,b]$ is revolved about the $x$-axis as shown in Figure 1.

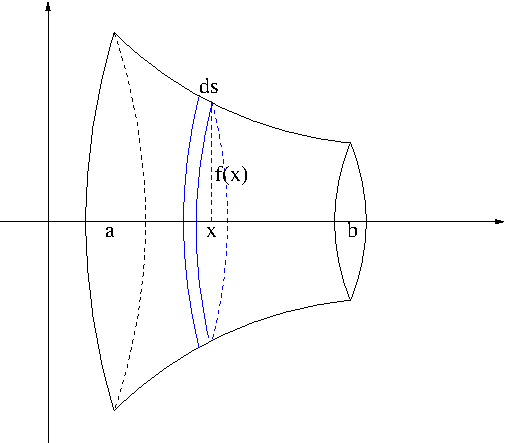
Figure 1

The area $A$ of the resulting surface of revolution can be obtained by adding (i.e. integrating) the areas of infinitesimally thin circular ribbons of radius $f(x)$ with thickness $ds$ at each $a\leq x\leq b$. \begin{equation}\label{eq:surfrev}A=\int_{x=a}^{x=b}2\pi f(x)ds=\int_a^b 2\pi f(x)\sqrt{1+[f'(x)]^2}dx\end{equation}

Example. Find the area of the surface generated by revolving $y=2\sqrt{x}$, $1\leq x\leq 2$ about the $x$-axis.

Solution. \begin{align*}A&=2\pi\int_1^2 2\sqrt{x}\sqrt{1+\left(\frac{1}{\sqrt{x}}\right)^2}dx\\&=4\pi\int_1^2 \sqrt{1+x}dx\\&=4\pi\left(\frac{2}{3}\right)[(1+x)^{\frac{3}{2}}]_1^2\\&=\frac{8\pi}{3}(3\sqrt{3}-2\sqrt{2})\end{align*}

Revolution about the $y$-axis

If $x=g(y)\leq 0$ is continuously differentiable on $[c,d]$, the area of the surface generated by revolving the curve $x=g(y)$ about the $y$-axis is \begin{equation}\label{eq:surfrev2}A=\int_c^d 2\pi g(y)\sqrt{1+[g'(y)]^2}dy\end{equation}

Example. The line segment $x=1-y$, $0\leq y\leq 1$ is revolved about the $y$-axis to generate a cone. Find its lateral surface area.

Solution. \begin{align*}A&=\int_0^1 2\pi(1-y)\sqrt{1+(-1)^2}dy\\&=2\sqrt{2}\pi\int_0^1(1-y)dy\\&=\sqrt{2}\pi\end{align*}

Surface are of revolution for parametrized curves

If a smooth curve $r(t)=(x(t),y(t))$, $\alpha\leq t\leq\beta$ is traversed exactly once as $t$ increases from $\alpha$ to $\beta$, then the surface area of revolution is given by:

1. Revolution about the $x$-axis ($y(t)\geq 0$) \begin{equation}\label{eq:surfrev3}A=\int_\alpha^\beta 2\pi y(t)\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\end{equation}
2. Revolution about the $y$-axis ($x(t)\geq 0$) \begin{equation}\label{eq:surfrev4}A=\int_\alpha^\beta 2\pi x(t)\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\end{equation}

Example. The circle $x^2+(y-1)^2=1$ of radius 1 centered at $(0,1)$ is parametrized as $$x=\cos t,\ y=\sin t+1,\ 0\leq t\leq 2\pi$$ Find the are of the surface swept out by revolving the circle about the $x$-axis.

Solution. Figure 2 shows the surface of revolution

Figure 2

and Figure 3 the same surface but for $-1\leq x\leq 0$

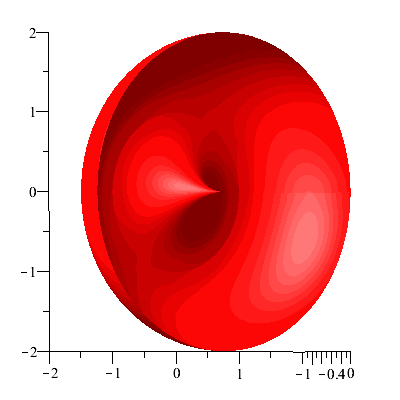
Figure 3

It is a doughnut shaped surface which is called a torus in mathematics. Using \eqref{eq:surfrev3} the area is given by \begin{align*} A&=2\pi\int_0^{2\pi}(1+\sin t)\sqrt{(-\sin t)^2+(\cos t)^2}dt\\&=2\pi\int_0^{2\pi}(1+\sin t)dt\\&=2\pi[t-\cos t]_0^{2\pi}\\&=4\pi^2\end{align*}