The Area of a Parallelogram

Let $v=(v_1,v_2)$ and $w=(w_1,w_2)$ be two linearly independent vectors in $\mathbb{R}^2$. Then they span a parallelogram as shown in Figure 1.

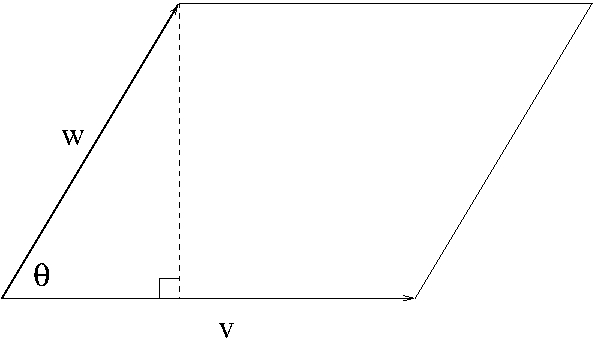
Figure 1. Parallelogram spanned by two vector v and w.

The area $A$ of the parallelogram is
$$\begin{align*} A&=||v||||w||\sin\theta\\ &=||v\times w||\\ &=\left|\begin{array}{cc} v_1 & v_2\\ w_1 & w_2 \end{array}\right|. \end{align*}$$
In general, the resulting determinant is not necessarily positive. If it is negative, we need to take the absolute value of the determinant for the area.

Exercise. Given two vectors $v=(v_1,v_2,v_3)$ and $w=(w_1,w_2,w_3)$ in $\mathbb{R}^3$, show that $||v||||w||\sin\theta=||v\times w||$ where $\theta$ is the angle between $v$ and $w$.

Hint. Note that $||v||^2||w||^2\sin^2\theta=||v||^2||w||^2-(v\cdot w)^2$.

The Volume of a Parallelepiped

Let $u=(u_1,u_2,u_3)$, $v=(v_1,v_2,v_3)$, $w=(w_1,w_2,w_3)$ be three linearly independent vectors in $\mathbb{R}^3$. Then they span a parallelepiped as shown in Figure 2.

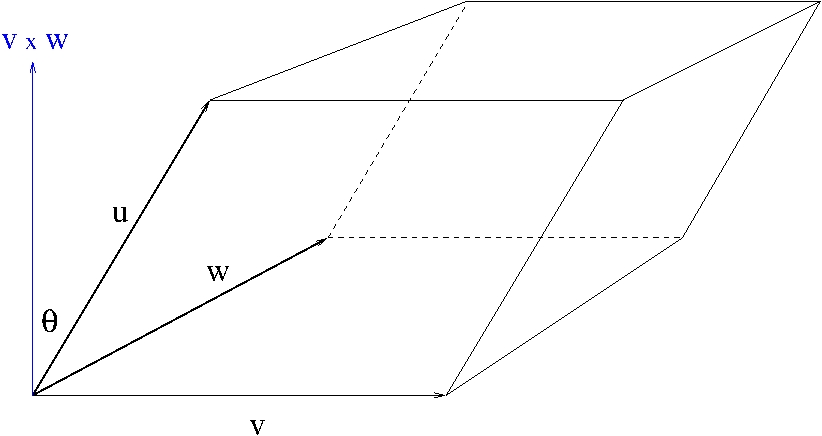
Figure 2. Parallelepiped spanned by vectors u, v and w.

The volume $V$ of the parallelepiped is
$$\begin{align*} V&=||u||\cos\theta ||v\times w||\\ &=u\cdot (v\times w)\\ &=\left|\begin{array}{ccc} u_1 & u_2 & u_3\\ v_1 & v_2 & v_3\\ w_1 & w_2 & w_3 \end{array}\right|. \end{align*}$$
In general, the resulting determinant is not necessarily positive. If it is negative, we need to take the absolute value of the determinant for the volume.