In the first lecture here, we defined a group. We have also seen an example of a group here, which is a symmetric group. In this lecture, we study some well-known examples of groups of finite and infinite orders. Recall that the order of a group os the number of elements in the group.

Examples of Groups

1. $(\mathbb{Z},+)$, $(\mathbb{Q},+)$, $(\mathbb{R},+)$, and $(\mathbb{C},+)$ are abelian groups of infinite order.
2. $(\mathbb{Q}\setminus\{0\},\cdot)$ is an abelian group of infinite order.
3. $(\mathbb{R}^+,\cdot)$ is an abelian group of infinite order. Here $\mathbb{R}^+$ denotes the set of all positive real numbers.
4. Let $E_n=\{e^{\frac{2k\pi i}{n}}: k=0,1,2,\cdots,n-1\}$. $e^{\frac{2k\pi i}{n}}$, $k=0,1,2,\cdots,n-1$ are the $n$-th roots of unity i.e. the zeros of $z^n=1$. $E_n$ forms an abelian group of order $n$. It is generated by a single element $e^{\frac{2\pi i}{n}}$. Such a group is called a cyclic group.

Definition. A group $G$ is said to be a finite group if it has a finite number of elements. The number of elements in $G$ is called the order of $G$ as mentioned previously and it is denoted by $|G|$ or $\mathrm{ord}(G)$. We use the notation $|G|$ for the order of the group $G$.

Example.Let $\mathbb{Z}_n=\{0,1,2,\cdots,n-1\}$. $\mathbb{Z}_n$ is the set of all possible remainders when an integer is divided by 2. The addition $+$ on $\mathbb{Z}_n$ is defined naturally as follows.
$$\begin{aligned}
\mathbb{Z}_2\\
\begin{array}{|c||c|c|}
\hline
+ & 0 & 1\\
\hline
\hline
0 & 0 & 1\\
\hline
1 & 1 & 0\\
\hline
\end{array}
\end{aligned}$$
$$\begin{aligned}
\mathbb{Z}_3\\
\begin{array}{|c||c|c|c|}
\hline
+ & 0 & 1 & 2\\
\hline
\hline
0 & 0 & 1 & 2\\
\hline
1 & 1 & 2 & 0\\
\hline
2 & 0 & 1 & 2\\
\hline
\end{array}
\end{aligned}$$
$(\mathbb{Z}_n,+)$ is an abelian group of order $n$. We will see later that the group $E_n$ and $\mathbb{Z}_n$ are indeed the same group.

Example. The set $M_{m\times n}(\mathbb{R})$ of all $m\times n$ matrices of real entries under matrix addition is an abelian group of infinite order.

Example. The set $\mathrm{GL}(n,\mathbb{R})$ of alll $n\times n$ non-singular matrices of real entries under matrix multiplication is a non-abelian group of infinite order. $\mathrm{GL}(n,\mathbb{R})$ is called the general linear group of degree $n$. It can be viewed as the set of all invertible linear transformations $T: \mathbb{R}^n\longrightarrow\mathbb{R}^n$ i.e. linear isomorphisms from $\mathbb{R}^n$ onto itself.

Example. [Klein four-group (Vierergruppe in German)]

Klein four-group

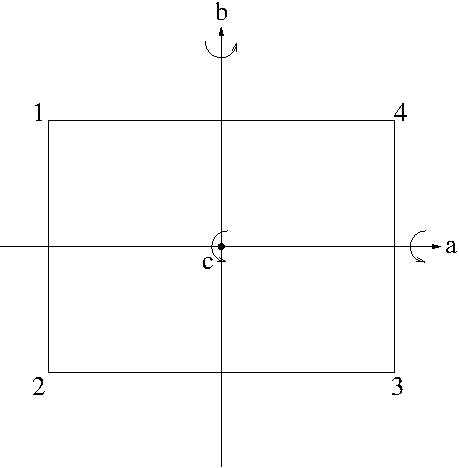
Let $V=\{e,a,b,c\}$ where $a$ is counterclockwise rotation of the rectangle in the picture about the $x$-axis by $180^\circ$, $b$ is counterclockwise rotation of the rectangle about the $y$-axis by $180^\circ$ and $c$ is counterclockwise rotation of the rectangle about the $z$-axis (the axis coming out of the origin toward you) by $180^\circ$. Then $a$, $b$ and $c$ satisfy the following relationship
\begin{align*}
a^2=b^2=c^2=e,\ ab&=ba=c,\ bc=cb=a,\\
ca&=ac=b.
\end{align*}
Here, $\cdot$ is the function composition i.e. successive application of rotations. By labling the vertices of the rectangle as 1, 2, 3, 4 as seen in the picture, we can define each rotation as a permutation of $\{1,2,3,4\}$.
\begin{align*}
e&=\begin{pmatrix}
1 & 2 & 3 & 4\\
1 & 2 & 3 & 4
\end{pmatrix},\ a=\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 1 & 4 &3
\end{pmatrix},\\
b&=\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 3 & 2 & 1
\end{pmatrix},\ c=\begin{pmatrix}
1 & 2 & 3 & 4\\
3 & 4 & 1 &2
\end{pmatrix}.
\end{align*}
For instance, we calculate $ab$:
\begin{align*}
ab&=\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 1 & 4 &3
\end{pmatrix}\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 3 & 2 & 1
\end{pmatrix}\\
&=\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 1 & 4 &3
\end{pmatrix}\begin{pmatrix}
4 & 3 & 2 & 1\\
3 & 4 & 1 & 2
\end{pmatrix}\\
&=\begin{pmatrix}
1 & 2 & 3 & 4\\
3 & 4 & 1 &2
\end{pmatrix}\\
&=c.
\end{align*}

Example. [The $n$-th dihedral group $D_n$, $n\geq 3$]

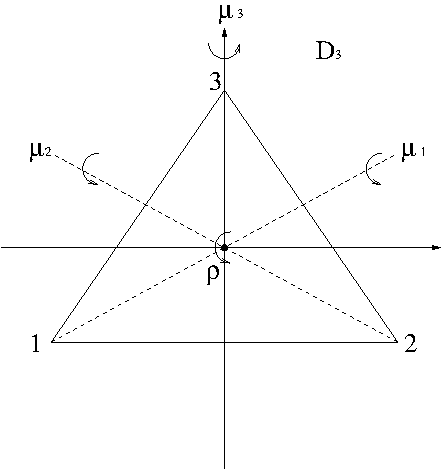
Consider an equilateral triangle shown in the following picture.

Dihedral group D3

$\rho$ is counterclockwise rotation about the axis coming out of the origin by $\frac{360^\circ}{3}=120^\circ$ and $\mu_i$, $i=1,2,3$ is counterclockwise rotation about the axis of rotation through each vertex $i$ by $180^\circ$. As permutations of the vertices $\{1,2,3\}$, $\rho$ and $\mu_i$ , $i=1,2,3$ are given by
\begin{align*}
\rho&=\begin{pmatrix}
1 & 2 & 3\\
2 & 3 & 1
\end{pmatrix},\ \mu_1=\begin{pmatrix}
1 & 2 & 3\\
1 & 3 & 2
\end{pmatrix}\\
\mu_2&=\begin{pmatrix}
1 & 2 & 3\\
3 & 2 & 1
\end{pmatrix},\ \mu_3=\begin{pmatrix}
1 & 2 & 3\\
2 & 1 &3
\end{pmatrix}.
\end{align*}
$D_3=\{e,\rho,\rho^2,\mu_1,\mu_2,\mu_3\}$ is a group called the 3rd dihedral group. $$\mu_1\mu_2=\rho^2\ne\rho=\mu_2\mu_1.$$
So, we see that $D_3$ is not an abelian group. $D_3$ is the group of symmetries of an equilateral triangle.

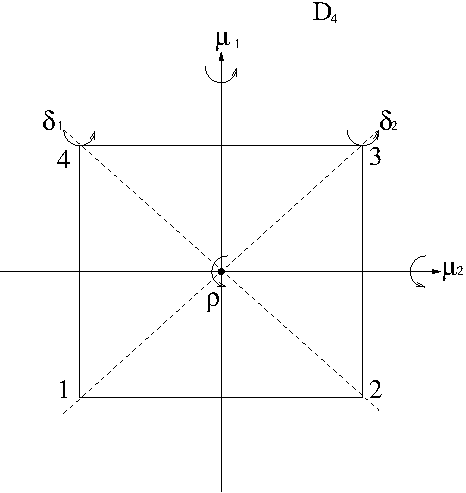
Now this time let us consider a square as shown in the following picture.

Dihedral group D4

$\rho$ is counterclockwise rotation about the $z$-axis coming out of the origin by $\frac{360^\circ}{4}=90^\circ$. $\mu_i$, $i=1,2$ are counterclockwise rotations about $y$-axis and $x$-axis, respectively by $180^\circ$. $\delta_i$, $i=1,2$ are counterclockwise rotations about the axis through the vertices 2 and 4 and the vertices through 1 and 3, respectively by $180^\circ$. As permutations of the vertices $\{1,2,3,4\}$, $\rho$, $\mu_i$ and $\delta_i$, $i=1,2$ are given by
\begin{align*}
\rho&=\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 3 & 4 & 1
\end{pmatrix},\\
\mu_1&=\begin{pmatrix}
1 & 2 & 3 & 4\\
2 & 1 & 4 & 3
\end{pmatrix},\ \mu_2=\begin{pmatrix}
1 & 2 & 3 & 4\\
4 & 3 & 2 & 1
\end{pmatrix},\\
\delta_1&=\begin{pmatrix}
1 & 2 & 3 & 4\\
3 & 2 & 1 & 4
\end{pmatrix},\ \delta_2=\begin{pmatrix}
1 & 2 & 3 & 4\\
1 & 4 & 3 & 2
\end{pmatrix}.
\end{align*}
$D_4=\{e,\rho,\rho^2,\rho^3,\mu_1,\mu_2,\delta_1,\delta_2\}$ is the group of symmetries of a square, called the 4th dihedral group. It is also called the octic group. Note that $|D_n|=2n$, $n\geq 3$.