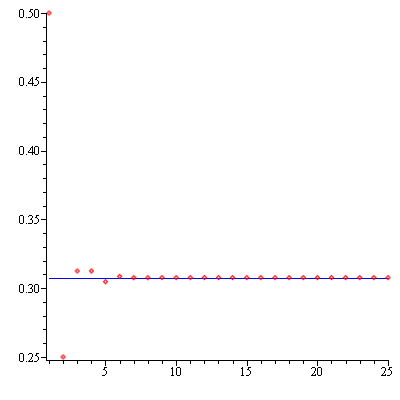The function $f(z)=\displaystyle\frac{1}{1+z}$ has an isolated singularity at $z=-1$. It has the Maclaurin series representation

$$f(z)=\sum_{n=0}^\infty(-1)^nz^n$$
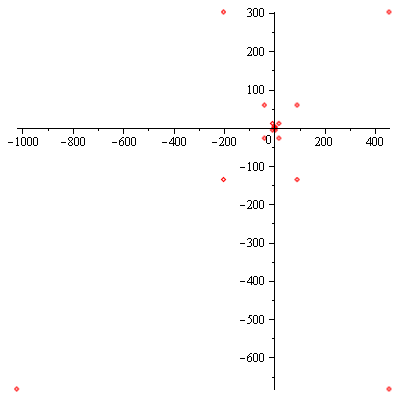
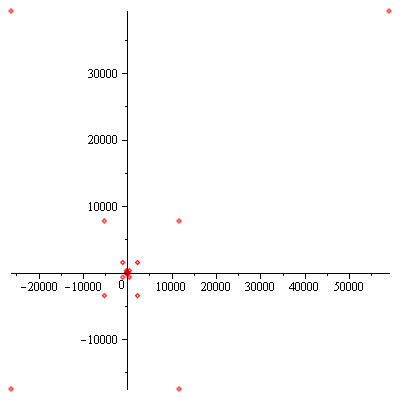
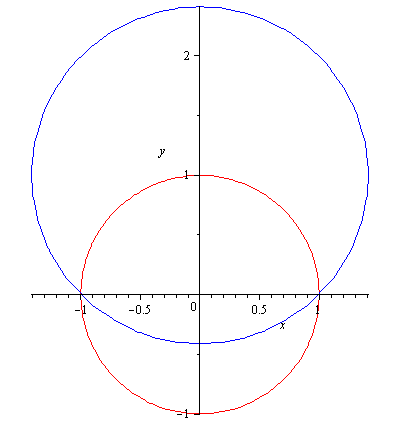
for $|z|<1$. The power series $f_1(z)=\displaystyle\sum_{n=0}^\infty(-1)^nz^n$ converges only on the open unit disk $D_1:\ |z|<1$. For instance, the series diverges at $z=\frac{3}{2}i$ i.e. $f_1\left(\frac{3}{2}i\right)$ is not defined. The first 25 partial sums of the series $f_1\left(\frac{3}{2}i\right)$ are listed below and they do not appear to be approaching somewhere.

S[1] = 1.
S[2] = 1. – 1.500000000 I
S[3] = -1.250000000 – 1.500000000 I
S[4] = -1.250000000 + 1.875000000 I
S[5] = 3.812500000 + 1.875000000 I
S[6] = 3.812500000 – 5.718750000 I
S[7] = -7.578125000 – 5.718750000 I
S[8] = -7.578125000 + 11.36718750 I
S[9] = 18.05078125 + 11.36718750 I
S[10] = 18.05078125 – 27.07617188 I
S[11] = -39.61425781 – 27.07617188 I
S[12] = -39.61425781 + 59.42138672 I
S[13] = 90.13208008 + 59.42138672 I
S[14] = 90.13208008 – 135.1981201 I
S[15] = -201.7971802 – 135.1981201 I
S[16] = -201.7971802 + 302.6957703 I
S[17] = 455.0436554 + 302.6957703 I
S[18] = 455.0436554 – 682.5654831 I
S[19] = -1022.848225 – 682.5654831 I
S[20] = -1022.848225 + 1534.272337 I
S[21] = 2302.408505 + 1534.272337 I
S[22] = 2302.408505 – 3453.612758 I
S[23] = -5179.419137 – 3453.612758 I
S[24] = -5179.419137 + 7769.128706 I
S[25] = 11654.69306 + 7769.128706 I

Also shown below are the graphics of partial sums of the series $f_1\left(\frac{3}{2}i\right)$.

The first 10 partial sums

The first 20 partial sums

The first 30 partial sums

Let us expand $f(z)=\displaystyle\frac{1}{1+z}$ at $z=i$. Then we obtain
\begin{align*}
f(z)&=\frac{1}{1+z}\\
&=\frac{1}{1+i}\cdot\frac{1}{1+\frac{z-i}{1+i}}\\
&=\sum_{n=0}^\infty (-1)^n\frac{(z-i)^n}{(1+i)^{n+1}}
\end{align*}
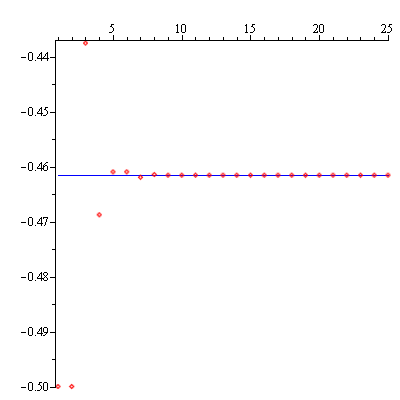
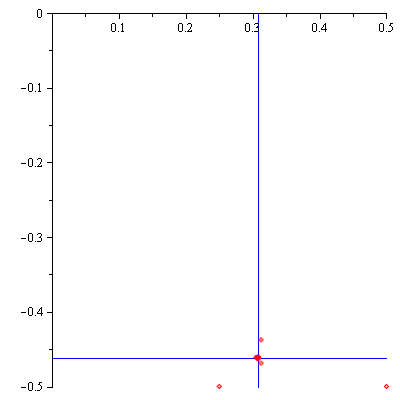
for $|z-i|<\sqrt{2}$. Let $f_2(z)=\displaystyle\sum_{n=0}^\infty (-1)^n\frac{(z-i)^n}{(1+i)^{n+1}}$. This series converges only on the open disk $D_2:\ |z-i|<\sqrt{2}$, in particular at $z=\frac{3}{2}i$ and $f_2\left(\frac{3}{2}i\right)=f\left(\frac{3}{2}i\right)=\frac{4}{13}-\frac{6}{13}i$. The first 25 partial sums of the series $f_2\left(\frac{3}{2}i\right)$ are listed below and it appears that they are approaching a number. In fact, they are approaching the complex number $f\left(\frac{3}{2}i\right)=\frac{4}{13}-\frac{6}{13}i$.

S[1] = 0.5000000000 – 0.5000000000 I
S[2] = 0.2500000000 – 0.5000000000 I
S[3] = 0.3125000000 – 0.4375000000 I
S[4] = 0.3125000000 – 0.4687500000 I
S[5] = 0.3046875000 – 0.4609375000 I
S[6] = 0.3085937500 – 0.4609375000 I
S[7] = 0.3076171875 – 0.4619140625 I
S[8] = 0.3076171875 – 0.4614257812 I
S[9] = 0.3077392578 – 0.4615478516 I
S[10] = 0.3076782227 – 0.4615478516 I
S[11] = 0.3076934814 – 0.4615325928 I
S[12] = 0.3076934814 – 0.4615402222 I
S[13] = 0.3076915741 – 0.4615383148 I
S[14] = 0.3076925278 – 0.4615383148 I
S[15] = 0.3076922894 – 0.4615385532 I
S[16] = 0.3076922894 – 0.4615384340 I
S[17] = 0.3076923192 – 0.4615384638 I
S[18] = 0.3076923043 – 0.4615384638 I
S[19] = 0.3076923080 – 0.4615384601 I
S[20] = 0.3076923080 – 0.4615384620 I
S[21] = 0.3076923075 – 0.4615384615 I
S[22] = 0.3076923077 – 0.4615384615 I
S[23] = 0.3076923077 – 0.4615384616 I
S[24] = 0.3076923077 – 0.4615384615 I
S[25] = 0.3076923077 – 0.4615384615 I

The following graphics shows that the real parts of the partial sums of the series $f_2\left(\frac{3}{2}i\right)$ are approaching $\frac{3}{14}$ (blue line).

The real parts of the first 25 partial sums

The next graphics shows that the imaginary parts of the partial sums of the series $f_2\left(\frac{3}{2}i\right)$  are approaching $-\frac{6}{13}$ (blue line).

The imaginary parts of the first 25 partial sums

Also shown below is the graphics of the first 25 partial sums of the series $f_2\left(\frac{3}{2}i\right)$. They are approaching the complex number $f\left(\frac{3}{2}i\right)=\frac{4}{13}-\frac{6}{13}i$ (the intersection of horizontal and vertical blue lines).

The first 25 partial sums

Note that $f_1(z)=f_2(z)$ on $D_1\cap D_2$. Define $F(z)$ as

$$F(z)=\left\{\begin{array}{ccc}
f_1(z) & \mbox{if} & z\in D_1,\\
f_2(z) & \mbox{if} & z\in D_2.
\end{array}\right.$$

Analytic continuation

Then $F(z)$ is analytic in $D_1\cup D_2$. The function $F(z)$ is called the analytic continuation into $D_1\cup D_2$ of either $f_1$ or $f_2$, and $f_1$ and $f_2$ are called elements of $F$. The function $f_1(z)$ can be continued analytically to the punctured plane $\mathbb{C}\setminus\{-1\}$ and the function $f(z)=\frac{1}{1+z}$ is indeed the analytic continuation into $\mathbb{C}\setminus\{-1\}$ of $f_1$. In general, whenever analytic continuation exists it is unique.